Topological photonics has gained significant interest during the last decade, and holds the unique potential to manipulate light in a disorder-free manner. Different models have been extensively studied to reveal the rich physical mechanisms of topological robust phases and offer diverse applications such as topological lasing and fault-tolerant quantum computing. To describe topological phases, global invariants like the Zak phase and Chern numbers are introduced. In recently years, several measurable methods of quantized Zak phases have been proposed and experimentally demonstrated to characterize topological states in two-band systems, for instance, the celebrated Su-Schrie?er Heeger (SSH) model.
Unlike a simple one-dimensional topological system like SSH model, multi-band superlattices provide richer topological features, of which the most intriguing feature is the multiple topologically nontrivial dispersion bands, meaning the number of topological edge states can be tuned by the inter-dimer couplings. This unique feature enables more ?exible control over the topological states.
Probing a general multi-band structure, which has proved experimentally challenging, requires a judiciously tailored Wannier function input excitation of the lattice. Rather surprisingly, in the case of a quadrimeric superlattice, a simplified experimental friendly bulk probing method is proposed to identify the topological character.
To address the problems, Quantum Nano Photonics (QNP) group led by Prof. Val Zwiller and Prof. Ali W. Elshaari from KTH Royal Institute of Technology (Sweden) realized a direct measurement of topological invariants in photonic superlattices.. The relevant research results were published in Photonics Research, Volume 12, 2022 (Ze-Sheng Xu, Jun Gao, Govind Krishna, Stephan Steinhauer, Val Zwiller, Ali W. Elshaari. Direct measurement of topological invariants in photonic superlattices[J]. Photonics Research, 2022, 10(12): 2901).
In this work, the photonic superlattice is carefully engineered with broken inversion symmetry, as shown in Fig.1(a), the superlattice consists of four sites per unit with uniform on-site potential. The superlattice model contains 3 bandgaps, as shown in Fig.1(b). When the intercell coupling is changed, the first and third bandgaps are never closed, while the bandgap centered at zero energy closes and reopens at a critical point . This bandgap number have different quantized values of 0 and π for different τ values in region I and region II. The beam displacement can be used to quantify the topological phases by monitoring the light propagation in the superlattice.
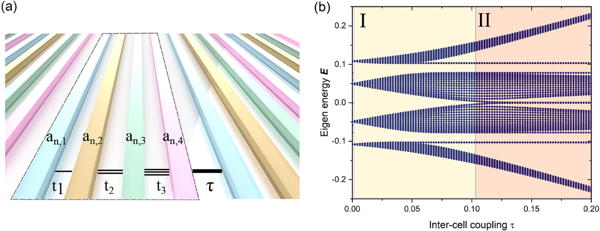
Fig. 1 (a) Schematic of SSH4 superlattice. (b) Energy spectrum for different inter-cell coupling τ values.
The research group used a CMOS-compatible Si3N4 photonic chip to implement the topological superlattice model. By tuning the intracell and intercell spacings, the fabricated superlattice would correspond to topological trivial and non-trivial phases. To detect light propagation in such nanosized waveguide array, the researchers raised a novel method to deliberately introduce scattering sites in each unit cell. The scattering sites are designed and fabricated in all the odd and even cells (separated by 5μm) to preserve the evolution fidelity.
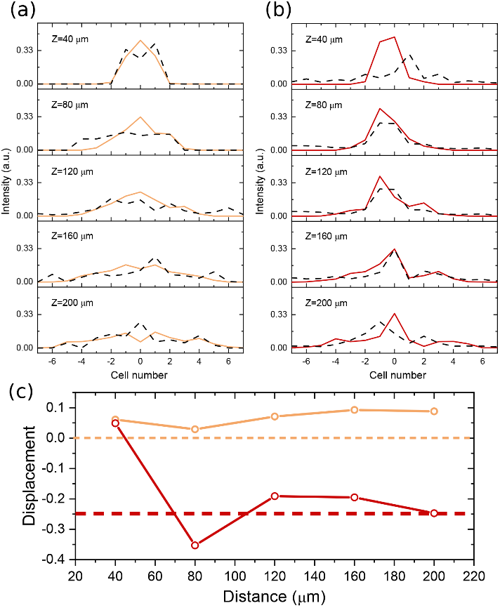
Fig. 2 (a) and (b) show the light intensity in different cells for trivial (gold) and non-trivial (brown) superlattices. (c) Measured beam displacement for trivial (gold) and non-trivial (brown) superlattices.
The scattered light can be captured by a top imaging system, and the evolution patterns at different propagation distances can be collected in a single sample with one-shot measurement. As shown in Fig.2(a) and (b), the measured light intensity for the trivial (gold) and non-trivial (brown) superlattice is compared with numerical simulation results (black dashed line). From the above intensity, beam displacement can be calculated as in Fig.2(c). The experimentally achieved beam displacement is 0.088 for the trivial superlattice and -0.245 for the non-trivial superlattice, which shows a good agreement with the theoretical values of 0 and -0.25. The measurements successfully reveal the direct probe of quantized topological phases in superlattices.
"This experiment offers a novel single-shot measurement of topological phases" says Prof. Ali W. Elshaari, "It will be exciting to combine our hybrid integration quantum circuits with topological photonics to explore topological phases into quantum regime." The results of this study will open up a new way to measure topological invariants in complex photonic structures in the future. The manipulation of multi-band structure may also provide a new resource to develop topologically robust quantum devices for integrated quantum photonics.







