Nonlinear photonic crystals can provide effective modulation for three-wave coupling processes, which is an important medium for laser wavelength expansion. The phase modulation in the transverse direction can also realize nonlinear wavefront shaping, which is significant in holographic imaging and quantum communication.

Vogel's spiral is a class of quasi-periodic structures, which is centrally symmetric in Fourier space. The spiral is defined by two polar coordinate formulas in which two key parameters, b and α, respectively determine the density of the elements and the polar angle between adjacent elements. When α is the golden angle, the Vogel's spiral evolves to sunflower structure and appears as a sharp ring in Fourier space. This characteristic has been reported in nonlinear photonic crystals to modulate broadband Cherenkov-type frequency doubling process. However, the Vogel's spirals have no solution on cascaded nonlinear processes, which limits the application in entangled photon generation and quantum communication.

In this work, the quasi-periodic spiral structure is proposed that can provide multiple circular reciprocal lattice vectors simultaneously. Three concentric frequency doubled rings are observed which modulated by this structure via nonlinear Raman-Nath diffraction.

The research group led by Dr. Tianxiang Xu and Prof. Yan Sheng from Ningbo University focused the combination of Vogel's spiral and quasicrystal theory and designed the quasi-periodic spiral. This structure can provide multiple circular reciprocal lattice vectors simultaneously. Three concentric frequency doubled rings are observed which are generated via nonlinear Raman-Nath diffraction. The research results are published in Chinese Optics Letters, Vol. 23, Issue 3, 2024: Jing Zeng, Sen Wang, Ruwei Zhao, Yongxing Liu, Tiefeng Xu, Yan Sheng, Tianxiang Xu. Nonlinear photonic quasi-periodic spiral[J]. Chinese Optics Letters, 2024, 22(3): 031902.

The two parameters b and α of Vogel's spiral are rearranged by using the cut-and-project method, their distribution in Fourier space is studied, and the relationship between Fourier spatial distribution and quasicrystal structural parameters is systematically analyzed. The results show that after rearranging the elementary density b according to the quasicrystal design method, the concentric ring radius of the obtained structure in Fourier space is related to the quasicrystal structure parameters.

The designed spiral was prepared by femtosecond laser induced ferroelectric domain inversion.

The experimental results of frequency doubling are in agreement with the theoretical prediction, which confirms the feasibility of the proposed method. Further, the quasi-periodic spiral which can modulate cascaded third harmonic generation in the communication band is designed.

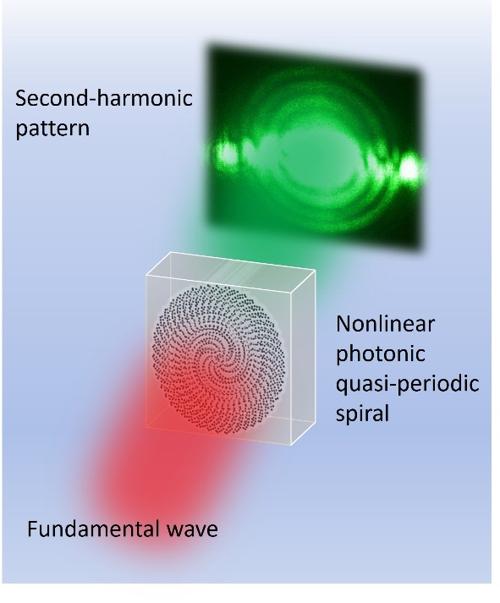
Fig. 1 Diagram of three-channel ring-like second harmonic generation modulated by quasi-periodic spiral