Recently, a review paper titled "Comprehensive review on developments of synthetic dimensions" was published in the Issue 2 of Photonics Insights, 2025. (Danying Yu, Wange Song, Luojia Wang, Rohith Srikanth, Sashank Kaushik Sridhar, Tao Chen, Chenxi Huang, Guangzhen Li, Xin Qiao, Xiaoxiong Wu, Zhaohui Dong, Yanyan He, Meng Xiao, Xianfeng Chen, Avik Dutt, Bryce Gadway, Luqi Yuan. Comprehensive review on developments of synthetic dimensions [J]. Photonics Insights, 2025, 4(2): R06.)
The concept of synthetic dimensions, which was brought in a decade ago, has quickly experienced a large development in the community of atomic, molecular, and optical physics as well as photonics. It shows a powerful framework that enables the exploration of high-dimensional physics beyond conventional spatial constraints. This review provides an emergent summary on past progresses in synthetic dimensions, discusses advantages and limitations on different approaches, and gives perspectives on the future developments. This review article could serve well for researchers who are already in this specific community but more importantly give a guideline for people who are new to the field to lead more fruitful results in interdisciplinary research in quantum simulation, atomic and photonic engineering, and information processing.
1. Introduction to Synthetic Dimensions
Quantum simulation of topological physics, non-Hermitian systems, and many-body interactions has brought great attention in modern physics. Although there are numerous physical platforms in atomic, molecular, and optical experiments, there exists the desire for new dimensionality beyond the conventional spatial dimensions to overcome constraints on higher-dimensional quantum simulations and novel manipulations of physical states. The concept of synthetic dimensions serves this task.
Different from spatial dimensions, synthetic dimensions usually rely on various degrees of freedom of a physical system, such as frequency, time in optical fields and the intrinsic states of atoms. However, the dynamics of a physical model can still be emulated in a space including this extra synthetic dimension. These key ideas leveraging such additional degrees of freedom to construct synthetic dimensions enable quantum simulations of high-dimensional Hamiltonians in low-dimensional systems or physical models that are otherwise difficult to be constructed in spatial space. This innovative framework therefore not only can break spatial limitations but also grants extra flexibility in bringing connectivity in models, facilitating the realization of many unusual features like effective gauge fields for bosonic particles, non-Hermitian couplings, and long-range interactions.
It has been recently noticed that there are two major categories for constructing synthetic dimensions (see Fig. 1). One is to use the discrete physical modes of light or atoms and connect them in an order to construct the synthetic dimension. In this way, the wave packet evolving on these modes follows a certain physical model usually in the tight-binding limit. The connectivity that is built in the synthetic dimension can hold the advantages of tunability and reconfigurability that are hard to realize in systems in real space. Another idea to construct the synthetic dimension is to use a system parameter in a geometric structure and relate it to a variable in a target Hamiltonian. Therefore, by varying the system parameter, the Hamiltonian of interest can be tuned in simulations. Usually, this variable is chosen as the momentum reciprocal to a particular spatial dimension in the Hamiltonian.
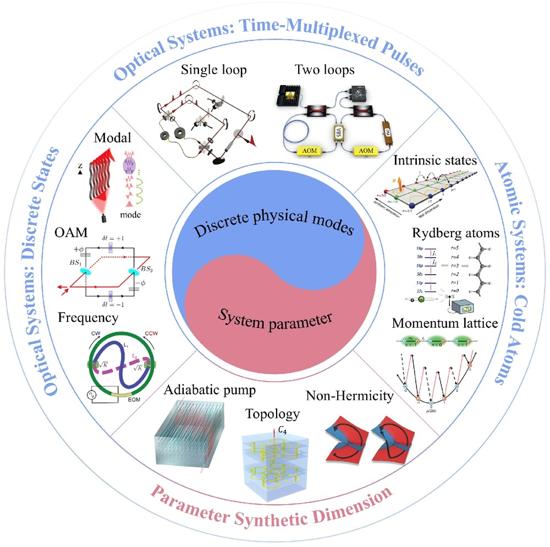
Fig. 1 Research landscape of synthetic dimensions.
2. Synthetic Dimensions in Photonic Systems
The tight-binding model probably is the simplest way to study many interesting physical phenomena in condensed matter systems, which has also been widely used in photonic systems with the aid of coupled-mode theory. In order to build synthetic dimensions in photonic systems, the key ingredient here is to determine appropriate discrete optical modes and then find a way to connect them in order. In this way, each optical mode can be considered as a potential well in the tight-binding model while the connectivity between them corresponds to the hopping of particle between two potential wells, so one can successfully build a tight-binding model but on a synthetic dimension (see Fig. 2). There are various degrees of freedom for optical fields that we can use to construct synthetic dimensions including frequency, orbital angular momentum, modal dimension, polarization, time, and more. It turns out that the advantage of constructing synthetic dimensions here is from the connectivity in designs, as it is highly tunable. As a result, one can introduce effective gauge potentials for photons, non-reciprocal interactions, and other exotic effects in physical models more easily, thus offering novel platforms for simulating high-dimensional topological states and studying non-equilibrium evolutions of optical fields. Moreover, these approaches also unlock new avenues for manipulating different degrees of freedom of light, with possible implications for optical communications and information processing.
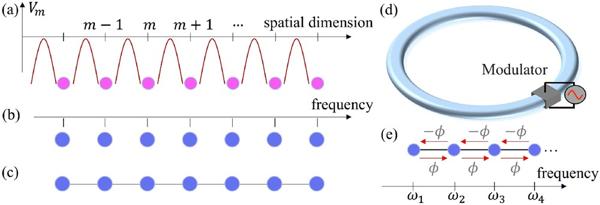
Fig. 2 Principle of synthetic frequency dimensions.
Beyond discrete photonic states, synthetic time dimensions constructed via connecting pulse arrival times based on a time-multiplexed network in single/double optical loops (see Fig. 3) are slightly different in their dynamics. To some extent, one can understand synthetic time dimension from the physical picture of quantum walks. Nevertheless, studies on synthetic time dimension also have achieved remarkable progress. In single-loop time-multiplexed lattices, phenomena like Ising machine simulations, dissipative topological photonics, and quantum walks have been observed. As for dual-loop systems, which may provide richer parameter tunability, studies on non-Hermitian phase transitions, thermodynamic analogs, and quantum-classical walks have been garnered broad attention. In particular, the inclusion of nonlinear effects in synthetic time lattices may also bring the future promise for soliton gas sensing and optical neural networks.
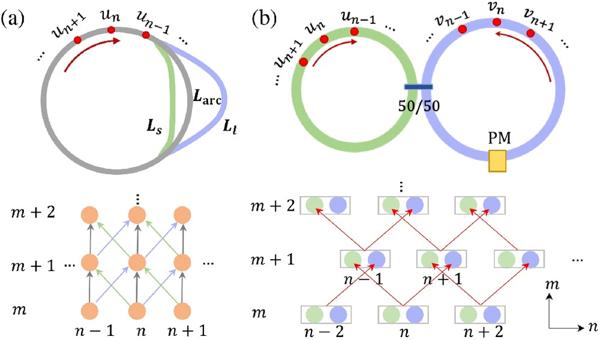
Fig. 3 Synthetic time dimensions in single/double-loop systems.
3. Synthetic Dimensions in Atomic Systems
The development of synthetic dimensions has also been very widely studied in atomic systems. In these platforms, intrinsic atomic states can be used to build the extra dimensionality by constructing the connectivity from driving external lasers and electromagnetic fields (radio frequency and microwave) on atoms. The field of atomic synthetic dimensions spans from low-energy atomic states, laser-excited metastable states and Rydberg states, to discrete states of atomic motion. For example, in Fig. 4, one can see that in a one-dimensional optical lattice confining ⁸⁷Rb atoms, one connects internal states (e.g., Zeeman sublevels) from Raman transitions to construct an additional synthetic dimension, so a hybrid two-dimensional lattice is formed. The synthetic dimensions with atomic systems are undergoing exciting studies and advances, where the atomic platform may naturally allow to bring particle-particle interactions and hence provides important approaches to performing many-body quantum simulations.
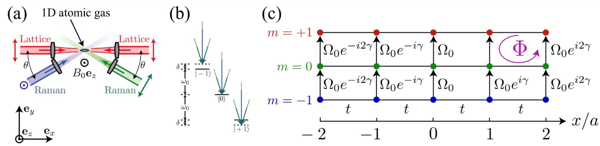
Fig. 4 Synthetic dimensions from atomic eigenstates.
4. Parameter Synthetic Dimensions
Different from the first category in building synthetic dimension, another category for synthetic dimensions is to use the system parameters. To understand the brief idea, one can consider a target Hamiltonian 𝐻(𝑝) dependent on a continuous variable 𝑝. It can be interpreted as the introduction of a 𝑝-axis as a synthetic dimension. In the design of real structures, one needs to use a system parameter to mimic the variable 𝑝. Therefore, higher-dimensional Hamiltonians can be constructed in structures with low dimensionality. We can take the Aubry-André model as illustration. One can introduce a system parameter ϕ to label the spacing distribution in a one-dimensional waveguide array as shown in Fig. 5. By an appropriate design of the parameter ϕ, one can link it to the momentum in the Hamiltonian of the Aubry-André model, so if the parameter ϕ is changed, the momentum of the Hamiltonian is varied effectively. It has been shown that one can tune the distribution of waveguide arrays along its propagation direction so that the parameter ϕ or the momentum of the Hamiltonian experiences an adiabatic variation. Therein, the optical field has been noted to experience an edge-bulk-edge transition, where a two-dimensional adiabatic pumping is demonstrated. Although the idea for constructing parameter synthetic dimension is different, such that a particle cannot be in a superposition of the degrees of freedom associated with the variable 𝑝, it can still bring useful methods for simulating complicated physical models and seeking novel light manipulation through its simpler designs in experiments.
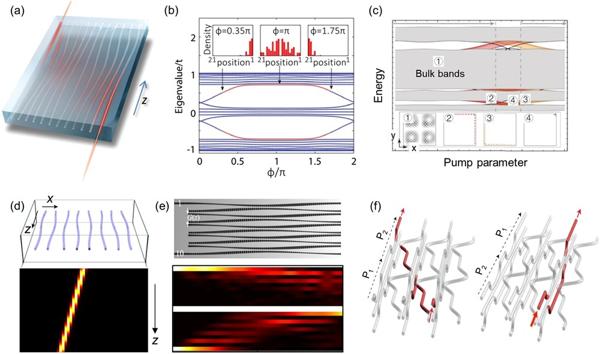
Fig. 5 Topological adiabatic pumping in waveguide lattices.
5. Outlook
This article reviews the concept of synthetic dimensions and numerous physical phenomena explored therein, expanding the discussion from optical and photonic systems to atomic and molecular systems. In particular, different aspects from various methods such as synthetic frequency dimension in photonics, time-multiplexed networks, intrinsic atomic states or momenta are compared to see the uniqueness of each method as well as their advantages and limitations in performing quantum simulations and studying novel topological and non-Hermitian physics.
The authors note that the field of synthetic dimensions is continuing to grow very rapidly now, with numerous significant contributions from the broader physical sciences community still emerging as this review is being written. With growing demands in quantum simulations and physical state manipulations, diverse platforms will unlock broader applications, particularly in fields of topological quantum computing, many-body physics, and integrated photonics. Advances in ultracold atoms and nanophotonics promise to translate theoretical designs into experimental realities, driving innovations in quantum technologies. This comprehensive review not only serves the purpose of summarizing representative past achievements in synthetic dimensions but more importantly triggers a broad interest from scientists from different communities, so more theoretical ideas can be catalyzed in an interdisciplinary way and more experiments can be achieved to join the innovation of quantum technology in the near future.







