Numerous breakthroughs in laser technology, such as the development of chirped pulse amplification (CPA), have revolutionized the field of high-power laser systems^[1^]. These advancements have enabled the creation of increasingly powerful laser facilities, capable of generating extreme peak powers and driving new experiments across a variety of scientific domains^[2^–9^]. As a result, multi-petawatt lasers have become a cornerstone of modern experimental physics^[10^], demanding precise engineering and optimization. These systems grow more complex, so does the need for accurate simulations to predict and control their behavior.

This study introduces a simulation framework based on the Frantz–Nodvik^[11^] equation to model the amplification process^[12^] across multiple amplifiers^[13^] within the High Power Laser System (HPLS) at the Extreme Light Infrastructure - Nuclear Physics (ELI-NP) facility. The framework is driven by a Python-based code at its core. The framework also includes an optimization algorithm to fine-tune amplifier parameters for better alignment with physical measurements, along with a simulation of back-reflection (BR) amplification originating from experimental targets. In this paper, we propose using these tools to optimize the pumping of amplifiers, reducing the amplification of BR while keeping the accumulated nonlinear phase distortions (B-integral) within safety margins. This approach provides a valuable method for enhancing the performance of high-power laser systems while ensuring machine safety against BR light from the experimental chamber^[14^,15^].

A critical aspect of managing high-power laser systems is mitigating optical damage caused by BR or the B-integral, to which optical elements operating near their damage thresholds or with anti-reflective coatings are particularly susceptible. The combination of accumulated phase distortions and high laser intensities leads to the formation of hot spots, which degrade beam quality and stability, posing substantial risks to system performance and safety, especially during the final stages of amplification. In contrast, BR presents a greater risk to optical elements near the front-end of the laser chain. Here the operational beam diameters are smaller and the potential for the BR pulse to be amplified increases as it passes through the majority of the system. These factors are relevant as they directly determine the fluence on the optical components.

The HPLS and similar high-power laser systems implement plasma mirrors (PMs) in order to enhance the temporal contrast^[16^] on target and to suppress BR. This can be implemented as a stand-alone double-PM system, similar to the setups in the MPQ ATLAS, J-Karen and Trident laser systems^[17^,18^], or as a single PM or double PMs placed between the focusing mirror and the target, as tested in several campaigns at the HPLS. This approach comes with drawbacks related to the loss in energy, of several tens of percents, and also with the additional challenge to measure the focal spot, as PMs can be detrimental to the quality of the focus. Both these effects degrade the intensity in the focus. The alternative approach described here considers the reduction of the number of PMs used, or even their elimination from the setup, making full use of the pulse’s energy and of the good focus on target. In order to achieve this, one has to mitigate the BR-associated risks. This is achieved through accurate simulations of BR amplification that mitigate potential damage caused by it.

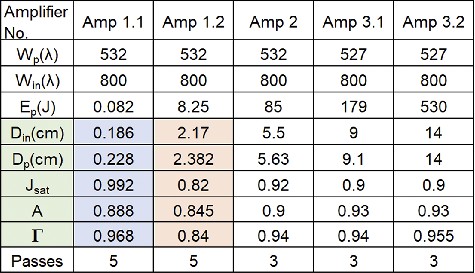
At the forefront of laser technology, the ELI-NP facility^[19^,20^] utilizes a hybrid CPA-optical parametric chirped pulse amplification (OPCPA) system^[21^] to achieve 10 PW peak power. The HPLS is constructed to deliver pulses of 100 TW, that is, 2.4 J at 24 fs with a repetition rate of 10 Hz by employing its first amplification stage consisting of a five-pass preamplifier and amplifier (later referred in the paper as Amp 1.1 and Amp 1.2, respectively). By further seeding the pulse into a subsequent three-pass amplifier (referred to as Amp 2) it can achieve 1 PW at 1 Hz repetition rate. A third stage of amplification can be employed, consisting of a three-pass preamplifier and amplifier (Amp 3.1 and Amp 3.2, respectively) to achieve peak power of 10 PW^[22^], that is, 240 J with 24 fs pulse duration at 1 shot per minute on target^[19^]. All amplification stages are pumped in a pulsed regime at 527–532 nm, which corresponds to the absorption band of Ti:sapphire crystals in the amplifiers. The amplification through the five multipass amplifiers is accompanied by sequential beam expanders to accommodate the beam’s fluence under the laser-induced damage threshold (LIDT)^[23^] across the laser systems. Starting with a beam diameter of only a couple of millimeters at the entrance of Amp 1.1, the beam exits from the optical compressor with 50 cm at the 10 PW level.

The design of amplifiers considers the necessity for flexible power output, ensuring that each amplifier can deliver the required energy for achieving 100 TW and 1 PW levels on target. When operating in the full amplification regime to reach 10 PW peak power, the former amplifiers function in a reduced state, providing just enough energy to seed the next amplifier. The first advantage is avoiding seeding unnecessary high energy in subsequent amplifiers: this strategy ensures a significantly increased lifetime of dozens of optical and electrical components, such as the flash lamps^[24^] and capacitors^[25^,26^] present mostly in pump lasers and amplification systems^[27^]. This in turn translates into a robust beam delivery pace with weeks of uninterrupted beam-time sessions while significantly reducing planned maintenance. Another crucial advantage is decreasing the accumulated nonlinear phase shift^[28^,29^] a laser pulse experiences as it passes through a medium with a nonlinear refractive index, such as Ti-sapphire crystals^[30^]:where B is the B-integral, $\lambda =800$ nm is the wavelength of the laser beam, ${n}_2$ is the nonlinear refractive index coefficient, $I(z)$ is the intensity of the laser beam along the propagation direction z and L is the total length of the laser medium over which the integral is evaluated^[31^]. It is evident that B-integral accumulation increases linearly with laser beam intensity. A high B-integral is undesirable for a laser beam as it indicates significant nonlinear phase distortion, which can degrade beam quality^[32^,33^], reduce focusability and lead to filamentation or large-scale self-focusing, damaging the optics and ultimately compromising the precision and effectiveness of the experimental results^[34^]. The downside of this mode of operation is lower extraction efficiency and increased residual gain (in the post-pulse regime), which can enhance the amplification of the BR light from a target. This phenomenon presents a potential danger to the laser system^[35^].

In an alternative scenario, increasing the pumping of solid-state amplifiers can, somewhat counterintuitively, lead to lower gain in the post-pulse regime. This occurs due to improved extraction efficiency as the amplifiers run in a more stable, saturated regime. This reduces the amplification potential for any BR light from the target. However, while this approach mitigates BR risks, it also increases the main laser beam intensity, leading to higher B-integral accumulation and, consequently, greater phase distortion. Therefore, it is crucial to find a careful balance between mitigating B-integral effects and minimizing BR amplification.

The Frantz–Nodvik equation is a well-established model for describing the amplification of laser pulses in a gain medium. The equation takes into account the saturation of the gain medium, allowing for accurate predictions of the energy output. The Frantz–Nodvik equation is as follows^[11^]: where ${J}_\mathrm{in}$ and ${J}_\mathrm{out}$ are the input and output fluences, respectively, typically measured in J cm ${}^{-2}$ , ${g}_0$ is the small signal gain, L is the length of the gain medium and ${G}_\mathrm{E}$ is the overall energy gain. Here, ${J}_\mathrm{in}$ can be calculated by dividing the input (or seed) energy by the beam cross-section area: ${J}_\mathrm{in}={E}_\mathrm{in}/\pi {r}^2$ .

The small signal gain can be expressed as follows: where ${J}_\mathrm{sat}$ is the saturation fluence, which is a property of the crystal. While for energy content it is a common practice to assign it a fixed value, in a spectral treatment the ${J}_\mathrm{sat}$ is dependent on both the seed’s wavelength and the crystal’s emission cross-section^[36^], as seen in Equation (4): where h is the Planck’s constant, c is the speed of light, $\lambda$ is the seed wavelength and ${\sigma}_{\lambda }$ is the emission cross-section of the crystal. Here, ${J}_\mathrm{stock}$ represents the absorbed pump fluence, which is linked to the quantum efficiency determined by the wavelength ratio between the seed ${\lambda}_\mathrm{in}$ and pump ${\lambda}_\mathrm{p}$ , as well as an arbitrary loss factor influenced by the crystal’s absorption of the pump beam A:

The crystal’s gain is dependent on the stored energy, meaning that ${J}_\mathrm{stock}$ will decrease with each pass due to the extraction process. Since all amplifiers are only pumped in a pulsed regime prior to the arrival of the main beam, there is no continuous replenishment of the stored energy. The updated absorbed pump fluence for the subsequent pass is given by the following:

This analysis is strictly limited to the energy domain and a potential limitation of the current methodology could be its omission of beam temporal chirp and its broad bandwidth (100 nm). However, these factors will be addressed in the next section. Theoretically, this would lead to an oversight towards prevalent phenomena in CPA systems, such as band narrowing^[37^] or red-shifting^[38^]. Practically, the physical system overcomes these unwanted phenomena by shaping the spectrum with a DAZZLER^[39^] – an acousto-optic turnkey ultrafast pulse shaping system that performs simultaneous and independent spectral phase and amplitude programming of ultrafast laser pulses prior to injection in the amplification chain and utilizing spectral filter mirrors in-between amplifiers. These measures are designed to selectively shape the beam’s spectrum and mitigate the spectral drift and spectral distortions.

Describing solid-state amplifiers through Frantz–Nodvik equations is reliable, as shown in previous work^[40^], with an error margin relatively that is low, within $\pm$ 5% per amplifier. Still, this error would quickly accumulate in a long amplification chain and should be further optimized for practical uses.

To achieve a more accurate representation of a real amplifier, energy measurements were collected for each pass through the amplifier while operating it at a specific pump energy level. This provides a reference table of actual energy measurements that can be used to align our simulation. This alignment involves fine-tuning a set of amplifier parameters to ensure the simulated energies closely match the real measurements. To this end, we developed a Python script that calls Equation (2) for each pass through the amplifier, using the known approximate input range for each parameter. The algorithm updates ${J}_\mathrm{in}$ and ${J}_\mathrm{stock}$ for each pass, as explained earlier.

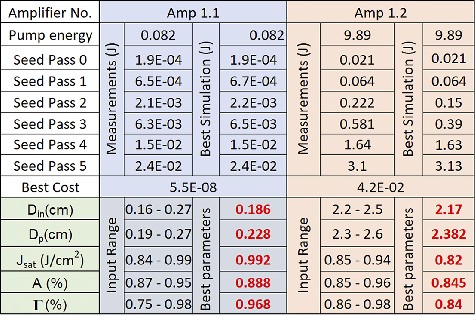
It is clear that a finer resolution – defined in this case as the step-size for scanning each interval – generates more accurate results by pinpointing precise input parameters while significantly increasing the execution time by the power of the number of scanning parameters (five in our case). To substantially increase this resolution while leveraging the execution time, we split the task into two stages. Initially, we run first a coarse search (e.g., with a resolution of 0.008) across the whole intervals of the rough known parameters of the amplifier. When the minimum coarse cost is found, a second run is performed with a much finer resolution (e.g., 0.002) over a tight interval (e.g., $\pm 0.02$ ) chosen automatically by the script located around the best set of parameters previously found. In summary, this brute-force algorithm operates in two steps: firstly, it identifies a coarse minimum, and then it refines the search to find a precise minimum. This efficiently determines the rough position of the global minimum, followed by refining its exact value. In this example, we scan across 6.12 million possible variations in the coarse run and 1.77 million in the fine run generating the best simulated data for Amp 1.2: 0.064, 0.15, 0.39, 1.63 and 3.13 J with a corresponding cost of $4.2\times {10}^{-2}$ J.

The technical description of our script is as follows: we utilize the $9\times 5$ table of input parameters (nine input parameters per amplifier across five amplifiers, as shown in Table 2) to feed an ‘AMP’ function that manages the simulation of each individual amplifier. Based on the acquired data, AMP calculates ${J}_\mathrm{in}$ and ${J}_\mathrm{stock}$ from Equation (5) and passes them down to a ‘PASS’ function that calculates the output fluence ${J}_\mathrm{out}$ (Equation (2)). Based on the current value ${J}_\mathrm{out}$ , AMP calculates the new ${J}_\mathrm{in}$ and ${J}_\mathrm{stock}$ using Equation (6) and passes them down again. As such, the amplification simulation of the whole HPLS is divided across two functions: AMP, which is responsible for one amplifier at a time, and PASS, which is responsible for one pass at a time within an amplifier. The logic scheme is presented in Figure 1. Relevant data such as output energy and residual gain are stored for later use.

To enhance the framework’s accuracy, we must account for a phenomenon present in Amp 1.2, thermal lensing. Pumping at high repetition rates and energy levels leads to the formation of a strong thermal lens. In the physical system, this thermal lens effect is compensated by injecting the seed with a relatively large divergence of $\approx$ 2 mrad. This approach is effective, but spreads the seed over an area larger than the pumped region, resulting in partial clipping of the beam at each pass through the crystal^[41^]. To simulate this clipping attenuation, we calculated the thermal lens of the crystal using Equation (7)^[42^,43^] and developed a simplified geometrical model that approximates the beam’s behavior through five apertures (corresponding to five passes), as seen in Figure 2:

where $\partial n/\partial T$ is the thermo-optic coefficient of the material ( $\approx 1.4\times {10}^{-5}\ {\mathrm{K}}^{-1}$ for Ti:sapphire), k is the thermal conductivity ( $\approx 0.4\;\mathrm{W}/\left(\mathrm{m}\cdot \mathrm{K}\right)$ for Ti:sapphire), A is the beam surface (m ${}^2$ ), ${P}_\mathrm{heat}$ is the applied pumping power ( $\approx 100$ W for Amp 1.2) and f = 32 m is the calculated focal length of the Amp 1.2 crystal lens.

Given the characteristics of the beam in Amp 1.2, we approximate the evolution of the beam with a geometrical approach and neglect diffraction. By dividing the pump area by the seed area at the entrance of the crystal, we obtain our attenuation factor for each pass. This approach ensures that the simulated energy attenuation due to clipping closely matches the real behavior observed in Amp 1.2.

The last step is to deal with a particular feature present in the last three stages of amplification. Due to their large volume, these crystals are prone to transversal lasing, a parasitic process that involves the amplification of light traveling perpendicular to the crystal axis, leading to the fast depletion of gain^[44^]. To mitigate transversal lasing, several strategies were tested, among which the most effective is sequential pumping: the crystal is partially pumped a couple of nanoseconds prior to seed’s arrival and then pumped again after each pass, while the seed performs its roundtrip through the bow-tie. This drastically reduces the peak gain responsible for emergence of transversal lasing by extending it over the whole duration of the amplification process. This feature is particularly important to implement in our framework, as it substantially alters the extraction process and the residual gain. The particular pump energies prior to each pass are well-known, highly tunable parameters and are specific to each crystal. To implement this in the script, we simply populate a $3\times 3$ table with pumping energies (3 passes $\times$ 3 amplifiers), which the AMP function utilizes when encountering those specific passes. This is done by adding in Equation (6) a term that accommodates an influx of energy when calculating ${J}_\mathrm{stock}$ : where ${J}_\mathrm{seq}$ is the fluence of the sequential pump.

The presented features accurately model the HPLS in the energy domain and serve as a solid basis for the integration of spectral analysis. To perform a spectral evolution across the amplification chain, we feed the script with a real spectrum of the seed extracted after the DAZZLER. The spectrum is then divided into 500 slices (or narrow wavelength ranges) and fed sequentially from ‘red’ to ‘blue’ into Equation (2) as ${J}_\mathrm{in}$ while updating ${J}_\mathrm{stock}$ after each iteration. In short, in our general amplification model, instead of injecting a stand-alone value representing the seed pulse for a single pass, we sequentially inject hundreds of small values, each representing a slice of our temporally chirped pulse. Moreover, by accounting for the crystal’s emission cross-section for each slice we can simultaneously emulate both the red-shifting and gain-narrowing phenomena. The crystal’s response to different wavelengths is represented by the variable ${J}_\mathrm{sat}$ , as shown in Equation (4). Here, ${J}_\mathrm{sat}$ will be calculated 500 times utilizing the central wavelength of each slice.

By integrating this feature into the amplification model and carefully tuning the input parameters, our framework achieves a faithful representation of the real laser system, capturing the nuances of the gain dynamics in both the energetic and spectral domains.

When all amplifiers have been accurately tuned and the amplification of the laser beam across the HPLS has been simulated, we can precisely track the intensity of the laser beam to calculate the accumulated B-integral. This is achieved by implementing Equation (1) within the amplification chain script.

The laser beam’s passage through the crystals is divided into 20 narrow spatial intervals for each pass. This resolution was carefully selected to balance computational efficiency with accuracy, as it faithfully captures the gradual increase in intensity during propagation through the crystals while keeping computation times manageable. Furthermore, tests with higher resolutions, such as 40 space intervals per crystal, revealed little difference in the calculated B-integral, confirming the adequacy of the chosen resolution.

The script iterates through all intervals and multiple passes for each crystal, accounting for their specific thicknesses. In addition to calculating the contribution to the B-integral from the crystals, the calculation also incorporates contributions from free propagation in air between passes and crystals, as well as from the 65 mm fused silica window used to inject the beam into the optical compressor placed in vacuum. Together, these components complete the total B-integral calculation. All the distances between passes and crystals were physically measured and entered into a table, which the script dynamically references during the computations.

After achieving a well-fitted model, the framework was extended to simulate BR propagation and amplification produced in an experiment by the interaction of the laser pulse with a thin foil target. This was done by seeding the beam back through the five amplifiers with an input energy level around hundreds of mJ, a value often observed from solid targets during the 10 PW experimental campaign utilizing our custom diagnostic devices built to capture BR. This BR amplification model takes into account the parameters stored in the input file (e.g., Table 2) while ignoring any pump energies. Only residual gain present in each crystal is considered. When estimating the residual gain, we must account for gain decay, which takes place during the beam’s round-trip travel from the crystal to the target and back. The distance from the target to the crystal ranges from 80 m for Amp 3.2 to 185 m for Amp 1.1, which corresponds to 530–1234 ns of beam travel time. From the fluorescence lifetime of the Ti:sapphire crystal $\tau$ = 3.2 μs, we can fit the delay as a gain loss using the following equation^[45^]:

This gives us a map of gain decay for all the crystals present in the system (as shown in Figure 3) and concludes the optimization of our model to track BR amplification. In an attempt to reduce this BR amplification cascade while exploiting the advantages of reduced pumping, we explored, in our simulation, various pumping regimes of the HPLS to observe its effect on a seeded BR beam of 0.35 J (equivalent to $\approx$ 0.2% reflected from target at 10 PW). The evolution of BR across the amplification chain for the four pumping scenarios chosen is shown in Figure 4 with their corresponding pumping energies and residual gain presented in Figure 5. The four scenarios are as follows. (1) Reduced pumping across all amplifiers – this simulates the currently utilized configuration of the HPLS to deliver 10 PW shots on target. (2) Pumping strongly only Amp 1.2 – this will increase the output energy of the main beam, which facilitates the extraction efficiency of both Amp 1.2 and Amp 2. This strategy should minimize present gain for BR light in both amplifiers. (3) Strong pump only in Amp 2 – it is observed that for a large range of BR energies, Amp 2 functions as a well-tuned preamplifier for Amp 1.2. By depleting the residual gain in Amp 2, we attempt to minimize this effect. (4) Strong pump in all amplifiers – this configuration ensures minimal residual gain/BR amplification in all amplifiers, disregarding all other tradeoffs.

Utilizing the presented tools we have successfully managed to overlap our amplification simulation of the HPLS (i.e., from the DAZZLER to Amp 3.2) with its real counterpart in both spectral and energy content, as seen in Figures 6(a) and 6(b), respectively.

To track the spectral evolution of the BR beam, we utilized the real spectrum of a BR light captured for a 1 PW shot through the leakage of a mirror and fed it through the amplification chain in the reverse direction. In Figure 4 we observe that Amps 3.1 and 3.2 have a high extraction efficiency due to a strong seed regardless of pumping energy therein. The main beam depletes the crystals almost completely in its last pass despite the presence of sequential pumping, which facilitates a high influx of energy prior to the last pass. Moreover, their large operating beam diameters, 95 and 150 mm, respectively, are unsuitable for small traces of BR and only above 1.3% of back-reflected energy from the target (i.e., a factor of seven larger than what is presented) is the impact on the amplification process noticeable. It is clear that the pumping energy is inversely proportional to the residual gain in each crystal. Similar to amplification, the B-integral accumulation in the main beam is a cascade: facilitating a good extraction efficiency in an amplifier (i.e., raising energy output) will lead to faster B-integral accumulation in all subsequent amplifiers, which, when seeded strongly will further improve energy output and B-integral accumulation. Therefore, fully pumping all amplifiers leads to the lowest BR amplification and highest $B=1.7$ , as shown in Figure 4. Fully pumping Amp 1.2 produces the second-best result, followed by fully pumping Amp 2, producing B-integral values of 1.24 and 1.11, respectively, while the currently used ‘reduced pump’ configuration performs the worst, having at best $B=1.04$ .

Although the BR spectrum is highly sensitive to the target type and experimental interaction conditions, the available data indicate that in this case the band is compatible with the HPLS as its modulation is insufficient for further filtering by the optical compressor or the high-reflectivity dielectric mirrors within the system. However, in certain situations, the BR spectrum may undergo changes due to Doppler shifts, stimulated Raman scattering (SRS) or self-phase modulation (SPM)^[46^], in which case the alteration in its shape becomes more significant.

By employing the CPA technique, the main beam propagates through the HPLS with a positive temporal chirp, which is later nullified by the optical compressor; the BR beam, prior to entering the amplification chain, will pass a second time through the optical compressor, which will imprint a negative chirp. To emulated the present negative chirp in this spectral analysis, the BR pulse was fed from ‘blue’ to ‘red’. As such, in Figure 7 we see that the evolution of the BR spectrum through the amplification chain is low, which is likely correlated with the relatively low energy gained, with a slight blue-shift.

This study presents a comprehensive simulation framework for modeling both the main and BR beam amplification in high-power laser systems using the Frantz–Nodvik equation. The framework incorporates a robust optimization process to fine-tune amplifier parameters and is customized for their specific characteristics ensuring close alignment with physical measurements. This encompasses spatial seed clipping caused by induced beam divergence (Figure 2), which helps mitigate thermal lensing, as well as sequential pumping, which distributes the deposited energy throughout the entire amplification process. BR amplification simulation highlights the impact of residual gain and gain decay. Its implementation in Python allows for a versatile and iterative approach where certain key areas are targeted for the purpose of monitoring the energy and fluence of the main and BR beams traveling through the HPLS. This allows us to identify the most susceptible optical components to laser-induced damage while leveraging the gain in different stages of amplification for the best beam on target while operating in the safest manner. The standard for the rated energy that each area in the HPLS can handle is based on a conservative fluence value of 2 J cm ${}^{-2}$ , which was chosen based on technical specification of the dielectric coatings present in the system. Applying the presented framework to the 10 PW laser system at the ELI-NP facility, we conclude that the best strategy for reducing the BR amplification while minimizing the B-integral is fully pumping Amp 1.2. This will protect most of the HPLS, with the exception of Amp 1.1, which cannot be protected from hundreds of mJ in BR by only tuning the system and requires implementation of an optical isolator. Two additional strategies were employed to reduce the back-reflected signal. Firstly, a PM was placed between the focusing optics and the target. Secondly, the thin-foil targets were positioned at angles of 15°–30° relative to the normal incidence of the laser beam. It could be argued that the coaxial alignment of BR light with the main beam is unlikely. Our observations during multiple experimental campaigns indicate that this alignment, in fact, commonly occurs. This highlights the relevance and importance of addressing the risk of BR in multi-PW laser systems. Future work will focus on further refining the model and exploring additional applications in high-power laser research, such as developing mitigation strategies for BR light.