Abstract
Light detection, no matter with human eyes or photodetectors, has long been limited by the dimensions of the obtained information. The term dimension refers to not only the three-dimensional space and the one-dimensional time but also physical quantities completely defining a light field such as amplitude, phase, polarization, and wavelength. Conventional light detections mainly capture two-dimensional transverse spatial intensity (amplitude), sometimes color or wavelength resolved, and great efforts have been taken to expand the optical sensing dimensions. As various types of novel structured light are enabled by advanced optical field manipulation approaches, full-dimensional optical sensing of arbitrary light fields is highly demanded, to resolve three-dimensional spatiotemporal amplitude, phase, polarization, and wavelength information. Here we have proved the concept of high-dimensional one-shot optical field compressive sensing, resolving full-dimensional information of any light field. Besides ordinary light fields with spatiotemporally uniform polarization states, full-dimensional metrologies of complicated structured light are conducted, including optical vortices, radially and azimuthally polarized beams, polarization-gating fields. It is believed that this light detection framework can not only be further compactly implemented for high-dimensional one-shot light detectors, but also observe dynamic physical processes in real-time.
Introduction
Structured light is formed by manipulating the amplitude, phase, polarization, and wavelength of light fields in multiple spatiotemporal dimensions1, revealing intrinsic freedom degrees of photons for broad applications2. To capture rich information on such complicated optical fields in one exposure, high-dimensional optical sensing is proposed3. For spatially structured light with 2D transverse features4,5, arrayed photodetectors with metasurfaces resolve spatial profiles of intensity and polarization6,7,8, and wavefront phase profiles are complemented for complete 2D optical field metrology9,10. As studies of structured light have been progressing beyond 2D, generation of 3D spatially or (3 + 1)D spatiotemporally structured light is generally equivalent to manipulating its 3D spatiotemporal vectorial optical field profile11,12,13
where ??,? and φ?,? are 3D amplitude and phase profiles of ?- and ?-polarized components along orthogonal unit vectors ?? and ??, respectively. The 3D polarization state is therefore marked by the amplitude ratio angle ?(?,?,?)=tan−1[??(?,?,?)/??(?,?,?)] and the phase difference Δ(?,?,?)=φ?(?,?,?)−φ?(?,?,?) between ?- and ?-polarized components14.
The sensing of 3D spatiotemporal or spatiospectral scalar field profiles without specific polarization information has been extensively demonstrated. Using metasurface- or photonic crystal slab-based novel detectors, one can measure the 3D wavelength ?-resolved spatiospectral intensity profile ?(?,?,?) in one shot15,16; however, neither the spectral nor the spatial wavefront phase is available. To measure the phase in single-shot, diffractive optical elements (DOE), spatially multiplex a few spectral slices of the incident light onto a single arrayed detector, resolving the 3D amplitude and phase profiles of scalar fields and being sensitive to simple linear polarization variations17,18,19,20. The combination of a micro-lens array and a multi-channel spectrometer also enables 3D spatiotemporal sensing of a scalar optical field with improved spectral resolution, but at the cost of spatial resolution21. Compressive sensing is also applied to high-dimensional optical sensing because its mathematical nature allows the one-shot detection of sparse signals in reduced dimensions22. 3D spatiospectral and spatiotemporal intensities have been measured with reasonable resolutions along all three dimensions using coded aperture snapshot spectral imaging (CASSI)23,24,25 and streak camera-enabled ultrafast compressive photography (CUP)26, or even simultaneously27,28. Phase information can be complemented by measuring the wavelength or time-sliced diffraction intensity patterns using CASSI or CUP, realizing the complete 3D characterization of a linearly polarized scalar field29,30.
However, one should always keep in mind that light is a transverse vectorial electromagnetic wave; 3D scalar optical field measurements, ignoring the vectorial nature of light, are not applicable to complex structured light. Although technically challenging, novel approaches have long been investigated to measure 3D spatiospectral or spatiotemporal light polarization in a single shot. Compressive sensing of 3D polarization states with a polarization-sensitive coded mask or detector only determines the polarization direction of simple linearly polarized light31,32 or detects circularly or elliptically polarized states without chirality33,34,35. Recently, one-shot 3D light polarization measurement in the spatiospectral domain was achieved for the first time as a milestone using a dispersion-resolved metamaterial photodetector and a micro-lens array36. Soon after, spectro-polarimetric imaging cameras were realized in real time based on encoding metasurfaces37. However, in all the studies above31,32,33,34,35,36,37, only the 3D intensity profile is obtained together with the 3D polarization state information; the absence of 3D phase information φ?,? prevents the measurement of the genuine 3D vectorial optical field profile in one shot for complicated structured light, especially in the spatiotemporal domain.
Thus, to our best knowledge, high-dimensional one-shot sensing of an arbitrary light field, especially complicated structured light beyond 2D, is to be realized. In this article, we demonstrate a solution to this problem, realizing the compressive sensing of any vectorial optical field ?(?,?,?) in Eq. (1) with complete 3D spatiotemporal amplitude, phase, polarization, and wavelength information. To prove the concept, we first fully visualize femtosecond laser pulses with arbitrary linear, circular, and elliptical polarization states, which are less structured. Then, 2D structured light fields are fabricated and spatiotemporally measured in one shot, including optical vortices, radially and azimuthally polarized beams. For structured light beyond 2D, the high-dimensional one-shot optical sensing of a polarization-gating pulse with temporally varying polarization states is demonstrated.
Results
Principle of high-dimensional one-shot optical field compressive sensing
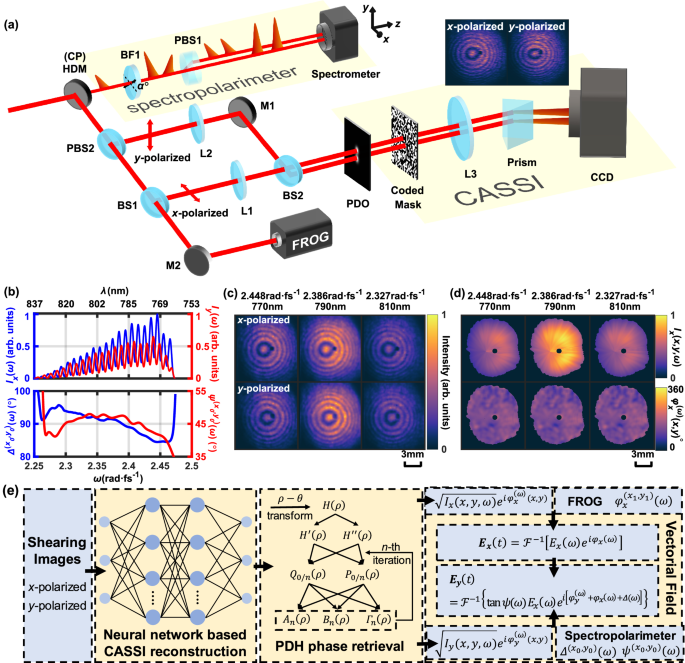
Figure 1a illustrates the principle of high-dimensional one-shot optical field compressive sensing. At the specific position where the incident light field is to be fully characterized, we define the checking point (CP) and place a flat, centrally hole-drilled mirror (HDM, 650 μm hole diameter). The transmissive light field is for polarization state measurement and is described by a 1D temporal profile sampling of ?(?,?,?) at the spatial position (?0,?0). The 1D light field ?(?0,?0,?) normally transmits through a birefringent crystal (BF1, 1.4 mm-thick ?-barium borate) whose optical axis has an angle of ? to the ?-direction, introducing a frequency-dependent phase retardation ?(?) between the ordinary and extraordinary polarization components. A polarization beam separation unit (PBS1) spatially offsets ?- and ?-polarized light, each of which includes a pulse pair with the phase delay ?(?). A home-made simple two-channel spectrometer simultaneously records spectral intensities of ?- and ?-polarized light (Fig. 1b top row)
Here one can select any optical axis angle ? of BF1 rather than 0°, 45°, 90°, so we simply set ?=30° in the experiment. Fringe analysis of the two-channel spectropolarimeter results ??(?) and ??(?) reveals spectral polarization states of the incident light represented by ?(?0,?0)(?)=tan−1|??(?)/??(?)| and Δ(?0,?0)(?) (Fig. 1b bottom row)38. Note the sampled light field only transmits through the hole drilled in the mirror before the absolute spectral polarization measurement, so the measurement accuracy is guaranteed without any deterioration to the incident polarization state by obliquely reflective or transmissive optical elements applied in previous experiments32,33,34, which is practically too sensitive to be well calibrated or compensated.
Fig. 1: Principle of high-dimensional one-shot optical field compressive sensing.
a The schematic experimental setup. The spectropolarimeter consists of a birefringent crystal (BF1), a polarization beam splitter (PBS1), and a homemade two-channel spectrometer. The coded aperture snapshot spectral imager (CASSI) includes a coded mask, an imaging lens L3, an angularly dispersive prism, and a charge-coupled device camera (CCD). CP: checking point; HDM: holed drilled mirror; PBS2: polarization beam splitter; BS1, BS2: beam splitters; M1, M2: reflective mirror; L1, L2: imaging lens; PDO: point-diffraction object; FROG: Frequency-resolved optical gating. b Spectropolarimeter results ??(?) and ??(?) (top panel) at (?0,?0), and reconstructed frequency-resolved polarization parameters ?(?0,?0)(?) and Δ(?0,?0)(?) (bottom panels). Corresponding wavelengths are labeled on top. c CASSI reconstructions for ?- (top row) and ?-polarized (bottom row) point-diffraction holograms at wavelengths of 770 nm (left column), 790 nm (middle column), and 810 nm (right column), with corresponding angular frequencies marked on top. d Point-diffraction holographic reconstruction results for ?-polarized light, including intensity ??(?,?,?) (top row) and spatial phase profiles φ?(?)(?,?) (bottom row) at wavelengths of 770 nm (left column), 790 nm (middle column), and 810 nm (right column). Data with normalized intensity <0.1 is neglected. e The 3D spatiotemporal vectorial optical field reconstruction procedure.
For the remaining light reflected from the hole-drilled mirror (HDM), ?- and ?-polarized light components are separated by a polarization beam splitter (PBS2), and transmitted through convex lenses L1 and L2, respectively. We place a point-diffraction object (PDO) close to the rear focal planes of L1 and L2, to measure spectrally resolved spatial phase profiles φ?(?)(?,?) and φ?(?)(?,?) of ?- and ?-polarized light. In actual experiments, the point-diffraction object is implemented by a liquid-crystal spatial light modulator, introducing two phase modulation spots (180 μm-diameter) at spatial centers of ?- and ?-polarized light, respectively. The wavelength dependency of the spatial light phase modulation is considered in spatial phase recovery, only introducing negligible contrast variations among point-diffraction holograms for different spectral components. As the modulated beams are imaged by L1 and L2 from the checking point (CP) to the coded mask (a chromium-coated fused silica plate with a random binary pattern), point-diffraction holograms with concentric ring patterns are formed. The 3D spatiospectral intensity profiles of ?- and ?-polarized point-diffraction holograms are captured by the CASSI system23,24, i.e., spatially modulated by the coded mask, imaged by a lens L3, spectrally sheared by the prism, and finally captured or spectrally integrated by a charge-coupled device (CCD, Fig. 1a inset). Here, the combination of point-diffraction holography and CASSI for 3D phase retrieval of φ?,?(?)(?,?) in the spatiospectral domain is an interferometric compressive imaging approach, different from previous 3D scalar field measurements relying on the whole-beam diffraction17,18,19,29,30. Therefore, any phase or polarization singularity in the 3D vectorial field profile of complicated structured light can be reliably resolved.
To process the compressive sensing data, we use a standard CASSI reconstruction algorithm based on self-supervised neural networks (details in the “Methods” section)39 to reconstruct the ?- and ?-polarized 3D spatiospectral point-diffraction holograms (Fig. 1c). Spatiospectral intensity profiles ??(?,?,?) and ??(?,?,?), as well as spatial phase profiles φ?(?)(?,?) and φ?(?)(?,?) can in principle be retrieved from corresponding point-diffraction holograms in Fig. 1c using commercial fringe analysis software40, but we developed a simple iterative algorithm instead (Fig. 1d, details in the “Methods” section). Finally, a small portion of the ?-polarized laser field transmits through the splitting mirror (BS1) and the reflective mirror (M2) to a home-made non-collinear frequency resolved optical gating (FROG) device41, and a genetic algorithm is applied to reconstruct the spectral phase φ?(?1,?1)(?) at an arbitrarily chosen spatial position (?1,?1)30,42. Now 3D spatiospectral phase profile of ?-polarized laser field is φ?(?,?,?)=[φ?(?)(?,?)−φ?(?)(?1,?1)]+φ?(?1,?1)(?).
Now we can calculate the 3D spatiospectral and spatiotemporal light field profiles. Fourier transformation along the spectral domain on ??(?,?,?)eiφ?(?,?,?) yields the 3D spatiotemporal profile ??(?,?,?)eiφ?(?,?,?) of the ?-polarized light field. For the ?-polarized light, the 3D spatiospectral phase profile is φ?(?,?,?)=[φ?(?)(?,?)−φ?(?)(?0,?0)]+φ?(?0,?0,?)+Δ(?0,?0)(?), and the amplitude one is ??(?,?,?)=??(?,?,?)??(?0,?0,?)/??(?0,?0,?)×tan??(?0,?0)(?). The complex amplitudes of ?- and ?-polarized light components unambiguously determine the 3D spatiospectral polarization state with a method different from previous approaches using metasurfaces36,37. The 3D spatiotemporal field profile ??(?,?,?)eiφ?(?,?,?) is obtained again through Fourier transformation on ??(?,?,?)eiφy(x,y,?), and complete light field information is obtained using Eq. (1). The data reconstruction procedure of the 3D spatiotemporal vectorial optical field is systematically illustrated in Fig. 1e, including all key calculation steps mentioned above.
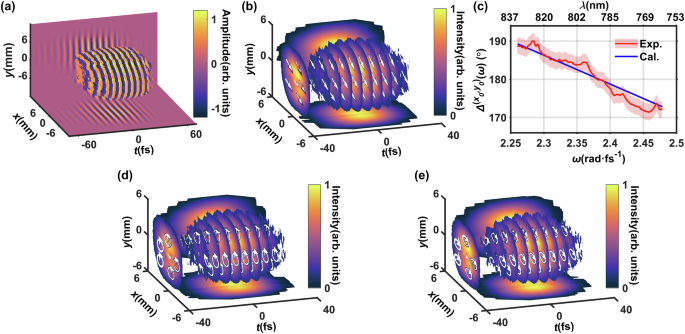
To prove the concept, we first generate less structured light fields with 3D homogeneous linear, circular, and elliptical polarization states, and test the capability of resolving 3D spatiotemporal amplitude, phase, polarization, and wavelength information. An ?-polarized, 800 nm, 40 fs laser pulse coming from a 1 kHz Ti:Sapphire laser amplifier transmits through a half-wave plate (WPZ2325-795 from Union Optics Inc.) whose optical axis is −15° to the ?-direction, so the output laser field is expected to be linearly polarized along -30° to the ?-direction. Figure 2a shows the actual field profile along the linear polarization direction with the carrier laser frequency reduced by 0.4 times for clear illustration. Meanwhile, the polarization directions of the laser field at selected time slices are labeled by white arrows around −30° to the ?-direction in Fig. 2b. The 3D intensity profile has a 38 fs temporal duration.
Fig. 2: High-dimensional one-shot optical sensing of homogeneously polarized light.
a The 3D spatiotemporal optical field profile of a femtosecond laser pulse with linear polarization −30° to the ?-direction. The carrier laser frequency is reduced by 0.4 times for clear illustration. b The 3D spatiotemporal polarization direction (white arrows) and intensity (color map) profiles of the linearly polarized femtosecond laser field for selected time slices. c The polarization parameter Δ(?0,?0)(?) describing the spectral phase difference between ?- and ?-polarized components of the linearly polarized femtosecond laser pulse, the red line is for the experimental (2.17° standard deviation shown in pink area) and the blue line for the calculation results. d and e The same as b, but for right-rotating circular (d) and left-rotating elliptical (e) polarizations.
Detailed studies show that the measured polarization phase difference Δ(?0,?0)(?) changes from 190° for the 2.26 rad/fs frequency component (834 nm wavelength) to 172° for the 2.48 rad/fs one (760 nm wavelength) (Fig. 2c red), consistent with calculations based on the half-wave plate refractive index provided by the supplier (Fig. 2c blue). Thus, the chromatic dispersion of the incident half-wave plate introduces wavelength–polarization coupling of a supposed linearly polarized light, illustrating the high-dimensional resolving power of the proposed scheme. In the time domain, the polarization state at each time slice is averaged over the entire spectral bandwidth, showing little variation.
We then use quarter-wave plates to generate light fields with right-rotating circular and left-rotating elliptical polarization, and Fig. 2d and e show their 3D spatiotemporal polarization states (white arrows) and intensities (color maps). For the elliptical polarization case, the white arrows form ellipses rotating along the left-hand direction, and their long axes are 20° to the ?-direction, consistent with the design. Moreover, the light chirality in each case is unambiguously determined, justifying the genuine 3D one-shot polarization resolving capability for arbitrary light, instead of simple specialized cases such as linear polarization33,34,35.
High-dimensional one-shot sensing of 2D structured light fields
As reviewed in ref. 1, 2D structured light refers to optical fields with a transversely ?–? spatial pattern of amplitude, phase, or polarization. One typical example is the optical vortex, which has a spiral spatial phase integer time of the azimuthal angle, physically representing the orbital angular momentum (OAM) of photons43. As optical vortices have broad applications in optical communications44,45,46, biological microscopy47, and quantum computation48, spatiotemporal vortices beyond 2D have even been demonstrated49,50.
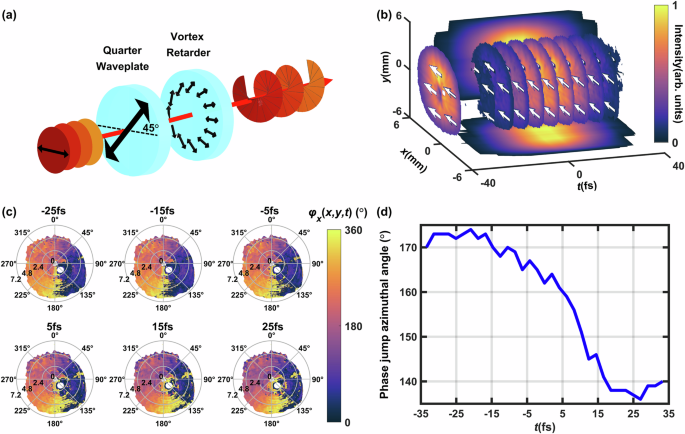
Here we conduct the high-dimensional one-shot sensing of a 2D optical vortex with +1 orbital angular momentum, which is generated by propagating an ?-polarized femtosecond laser pulse through a quarter-wave plate and a vortex retarder (Fig. 3a). Figure 3b shows the reconstructed 3D intensity profile, and as expected intensity singularities near the center of the beam profile are observed. The laser field has spatiotemporally homogeneous linear polarization along the ?-direction (Fig. 3b white arrows). The spatial phase profiles of the vortex field at different time slices (?= −25, −15, −5, 5, 15, 25 fs are presented in the polar coordinate (Fig. 3c). In each time slice, the phase linearly increases with the polar angle from 0° to 360°, indicating the +1 optical angular momentum as designed. In addition, the 360°–0° phase jump azimuthal angles at the radial position of 4.8 mm are plotted in Fig. 3(d) as a function of time, and the phase jump angle decreases rapidly from 170° to 140° during ?= −15 to 15 fs, but gradually during other time periods. The nonlinear decrease of the phase jump angle is related to the residual third-order spectral dispersion of the laser field. This complicated spatiotemporal phase–wavelength coupling effect proves the necessity of global high-dimensional optical field sensing.
Fig. 3: High-dimensional one-shot optical sensing of optical vortex fields.
a The schematic experimental setup for optical vortex generation, including a quarter-wave plate and a vortex retarder. b The 3D spatiotemporal polarization direction (white arrows) and intensity (color map) profiles of the optical vortex field. c Spatial phase profiles of the optical vortex field at time slices of −25, −15, −5, 5, 15, 25 fs. Data corresponding to normalized intensity <0.2 is neglected. The small white regions in the centers are singularity points, and those on the lower right side are due to the hole-drilled mirror HDM. d The 360°−0° phase jump azimuthal angle as a function of time, the radial position is 4.8 mm.
Another two important types of 2D structured light are radially and azimuthally polarized beams, which are applied to represent a novel complete set of quantum states51,52, accelerate high-energy particles53, image through biological tissues54, and fabricate three-dimensional microstructures55,56. We first generated the radially polarized beam by replacing the quarter-wave plate in Fig. 3a with a half-wave plate, whose optical axis is along the ?-direction and parallel to the incident laser’s linear polarization direction.
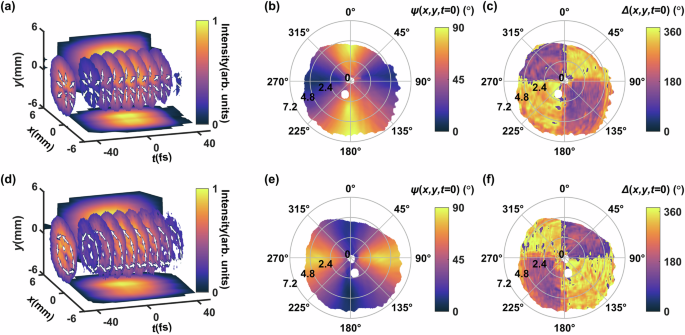
Figure 4a shows the reconstructed 3D spatiotemporal polarization directions, which are radially distributed (white arrows), as well as the intensity profile whose temporal duration is 40 fs close to the linearly polarized incident laser field. Intensity singularities are observed again along the two transversely spatial dimensions, similar to the case of an optical vortex. We take a representative time slice of the light field at ?= 0 fs, and ?(?,?,?=0) defining the angle between the local polarization direction and the ?-direction, which is plotted in the polar coordinate of Fig. 4b, confirming the radial polarization distribution. The phase difference Δ(?,?,?=0) between ?- and ?-polarization components is also plotted in Fig. 4c, around 360° in the 1st and 3rd quadrants but 180° in the 2nd and 4th quadrants as expected. Small discrepancies of Δ(?,?,?=0) from the designed values represent small ellipticities of the light field.
Fig. 4: High-dimensional one-shot optical sensing of radially and azimuthally polarized beams.
a The 3D spatiotemporal polarization direction (white arrows) and intensity (color map) profiles of the radially polarized beam. b The polarization parameter ?(?,?,?=0) describing the amplitude ratio angle between ?- and ?-polarized light components of the radially polarized beam. c The polarization parameter Δ(?,?,?=0) describing the phase difference between ?- and ?-polarized light components of the radially polarized beam. d–f The same as a–c, but for the azimuthally polarized beam.
To generate an azimuthally polarized beam, we rotate the half-wave plate with its optical axis along the ?-direction. The 3D spatiotemporal intensity and polarization profile are illustrated in Fig. 4d, showing polarization vectors pointing azimuthally. This observation is further corroborated by the detailed polarization angle map ?(?,?,?=0) and the phase difference map Δ(?,?,?=0) at the time slice of ?= 0 fs (Fig. 4e, f), consistent with the designed azimuthal polarization state.
High-dimensional one-shot sensing of structured light fields beyond 2D
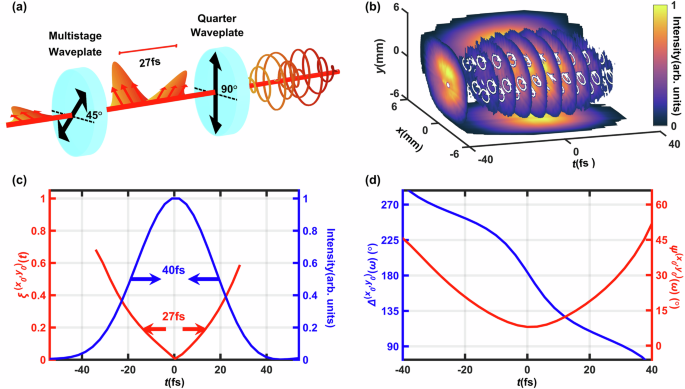
Control of structured light beyond 2D involves the manipulation of optical fields along the longitudinal temporal dimension. One typical example of such longitudinally structured light is the so-called polarization-gating field, which has counter-rotating circular polarization states at the leading and trailing edges of the pulsed light field, but is linearly polarized in the narrow central temporal region57. Polarization-gating fields have been applied for isolated attosecond electron and light pulse generation58,59, and chiral detection of biological molecules60. As shown in Fig. 5a, we generate the polarization-gating field by transmitting an ?-polarized 40 fs incident laser pulse through a birefringent crystal (~0.6 mm quartz with its optical axis at 45° to ?), introducing a 16 fs time delay between ordinary and extraordinary fields. Then a quarter-wave plate converts ordinary and extraordinary fields into left- and right-circularly polarized ones respectively, but in their temporally overlapping area, left- and right-circularly polarized fields coherently add up to form linear polarization.
Fig. 5: High-dimensional one-shot optical sensing of polarization-gating fields.
a Experimental setup for the polarization-gating field generation, including a birefringent quartz crystal (optical axis is 45° to the ?-direction) and a quarter-wave plate (optical axis is along ?-direction). b The 3D spatiotemporal polarization direction (white arrows) and intensity (color map) profiles of the polarized-gating fields. c The temporal intensity (blue line) and ellipticity ?(?0,?0)(?) (red line) of the polarization-gating field at the point (?0,?0). d The time-dependent polarization parameters ?(?0,?0)(?) and Δ(?0,?0)(?) at the point (?0,?0).
The high-dimensional one-shot sensing result of the polarization-gating field is illustrated in Fig. 5b, including the 3D intensity and polarization state distributions. Based on the spatiotemporal polarization state profile, the measured laser field polarization changes from left-rotating elliptical at ?= −30 fs to linear in a narrow time window around ?= 0 fs, and further to right-rotating elliptical as ? increases, until finally right-circular at ?= 40 fs. These experimental observations are consistent with the polarization-gating field theory57. As high harmonic attosecond light pulse generation efficiency is directly related to the ellipticity of the driving laser field, we calculate the time-dependent ellipticity of the measured polarization states of the vectorial polarization-gating laser field using ?=sin−1(sin?2?sin?Δ) (Fig. 5c). A gated temporal region with ?<0.2 for efficient high harmonic generation has a temporal duration is 27 fs, consistent with the theoretical prediction of 27 fs61. Further extending our proof-of-concept measurement to polarization-gating fields based on broadband few-cycle laser pulses is also feasible, thanks to the broad spectral coverage of CASSI.
Moreover, in most isolated attosecond light pulse generation experiments where the polarization gating technique is applied, the accurate linear polarization direction in the temporally narrow central gated region, as well as the generated attosecond light polarization direction, are hardly determined, because they are extremely sensitive to the thickness of the birefringent quartz crystal, ambient temperature, and other unexpected factors. Therefore, such ignorance of the polarization state of the attosecond light pulse degrades not only the accuracy of its spectral characterization using a grating, but also the degree of coherence after beam transportations through grazing reflective extreme ultraviolet optics for downstream applications. In contrast, Fig. 5d explicitly shows the longitudinally time-dependent polarization parameters ?(?0,?0)(?) and Δ(?0,?0)(?), and the direction of the central linearly polarized gated field (?) is 8° to the ?-direction. As far as we know, it is the first time to experimentally determine the polarization gating direction, potentially benefiting attosecond sciences.
Discussion
In summary, a technique has been demonstrated for completely measuring arbitrary light fields in one shot with amplitude, phase, polarization, and wavelength information distributed in the 3D spatiotemporal domain. One can further generalize such a technical scheme into a light detection framework called high-dimensional one-shot optical-field compressive sensing (HOOCS), enhancing conventional light detection capabilities (including human eyes) from 2D spatial intensity resolving, sometimes with color or wavelength information, to 3D spatiotemporal vectorial field resolving. In the HOOCS framework, a common 2D arrayed photodetector captures 3D spatiotemporal or spatiospectral intensity profiles of the incident light based on compressive sensing, each temporally or spectrally sliced 2D intensity profile encodes corresponding 2D transverse phase via coherent diffraction, and 1D longitudinal phase and polarization linking all temporal or spectral slices are finally measured by 1D sampling the incident light at a specific spatial location. Using this HOOCS framework, complicated 2D and 2D-beyond structured light has been fully characterized, including optical vortices, radially and azimuthally polarized beams, and polarization-gating fields, not to mention ordinary light, which is simple and less structured.
As a light detection framework, HOOCS can potentially be implemented in a compact and real-time way. For example, the angularly dispersive optics and the imaging lens in the compressive sensing CASSI system can be integrated into superdispersive metalenses, which significantly reduces the imaging distance62. In the 1D spectropolarimeter (Fig. 1a), the relatively bulky polarization beam separation (PBS1) unit can also be replaced by metasurfaces and then integrated into a hyperspectral arrayed detector10. In addition, for the computational method, recent advances in manifold learning have demonstrated enhanced reconstruction fidelity and computational efficiency in hyperspectral imaging63,64, showing the potential of real-time high-dimensional optical field sensing. Thus, one can expect compact and functional HOOCS light detectors as metamaterials and manifold learning to advance toward practical applications.
The HOOCS framework of light detection provides high-dimensional information about any light field, representing all necessary fundamental physical quantities, such as energy, momentum, spinal and orbital angular momenta of photons2,43,51,52. Regarding complicated structured light, even beyond 2D, HOOCS may be the only feasible diagnostic tool of light, as the frontiers of light field manipulation are being explored. It is especially important in large-scale laser facilities that structured light has been elaborately fabricated at an extremely low repetition rate and has significant shot-to-shot variation, and HOOCS can, in one shot, record the extreme physical process of energy, momentum, and angular momentum exchanges between exotic photons and fundamental particles of matter65.
Finally, optical metrology is equivalent to sensing a light field experiencing an object to be measured66, so one can take advantage of HOOCS’ high-dimensional optical sensibility to upgrade conventional metrological technologies. Following this logic, one-shot 3D scalar optical field measurement has already demonstrated its potential in conducting novel videographic reflectometry of ultrafast laser–solid interaction dynamics within attosecond time scales21. HOOCS is much superior to previous scalar field measurement techniques due to the vectorial nature of light, which, for example, has been utilized for high-sensitivity spectral ellipsometry of solid surfaces and thin films14. Thus, based on spatiospectral and spatiotemporal amplitude, phase, and polarization information provided by HOOCS, one can even expect advanced coherent videographic spectral ellipsometry for high-sensitivity, one-shot movies of ultrafast evolving interfaces, thin films, and low-dimensional materials. Similar HOOCS-based advancements of other optical metrological technologies, such as polarimetry and scatterometry, are being looked forward to as well.
Methods
The compressive sensing-based CASSI measurement of 3D spatiospectral intensity
CASSI stands for coded aperture snapshot spectral imaging, measuring a 3D spatiotemporal intensity profile of light23. As shown in Fig.1a, the spatiospectral intensity profile ?(?,?,?) is first spatially modulated by a coded mask ? (a pseudo-random binary pattern with 30?m×30?m pixel size), then sheared by an angularly dispersive optics (denoted by the operation of ?). Here we use a prism (PS850, Thorlabs, with angular dispersion of 14.3 nm/mrad@800 nm) placed at the Fourier plane of a 4-f imaging system with f1 = 125 mm and f2 = 100 mm. The sheared intensity profile is imaged by the 4-f imaging system onto the 2D array detector (HIKROBT CCD camera, MV-CA023-10UM, 5.86?m pixel size) and spectrally integrated (denoted by the operation of ?), yielding the 2D image ?(?′,?′). After discretizing the 3D intensity profile ?(?,?,?) and the 2D image profile ?(?′,?′) to an intensity cube ? and image signal B, the forward model can be expressed as ?=?? where ?=???. Mathematically, the task is to reconstruct ? from the measured ? with the given well-defined ?.
We use the plug-and-play deep image prior (PnP-DIP) algorithm for image reconstruction39, its main advantage is to use a self-supervised deep neural network for regularization. Thus, the mathematical expression of image reconstruction is
Here ||⋅||2 is the ?2 norm. The first term evaluates the distance between the estimated and measured results; the second and third terms are two imposed regulation functions. We use the total variation (TV) function as the ?(?) regulator in the second term and modify the weighting parameter ?67. The third term ?Θ(?) is the DIP regulator based on deep learning68, where ? is a random vector and Θ is the network’s parameters to be learned from ?. Normally, we use ?=0.001 and ?=0.1. The constrained optimization problem in Eq. (3) can be solved using well-established convex optimization algorithms, which have been implemented into open-access codes24.
Spatial intensity ??,?(?,?,?) and phase φ?,?(?)(?,?) reconstructions from frequency-resolved point-diffraction holograms
Point-diffraction holography is a powerful technique for spatial wavefront measurement69, and extensive algorithms have been developed and are available to retrieve amplitude and phase profiles40. Here, we develop a simple iterative algorithm to reconstruct spatial intensity ??,?(?,?,?) and phase φ?,?(?)(?,?) profiles from frequency-resolved point-diffraction holograms. For each frequency component, we first transform the point-diffraction hologram from the Cartesian coordinate to the square polar coordinate by defining ?=?2+?2 and ?=tan−1(?/?). The hologram ?(?) for each ? is calculated independently, and the interference fringe can be formulated as
where ?(?) and ?(?) are fringe background and fringe oscillation terms, ? is the fringe spatial frequency calculated by fitting the peaks and valleys of the interference fringe, ?(?) is the fringe phase. The first and second order derivatives of ?(?) are:
We introduce the intermediate variable ?(?)=−??(?)sin?(??+?(?)) and ?(?)=−?2?(?)cos?(??+?(?)), which are the leading terms of Eqs. (5) and (6) respectively. Meanwhile, all terms proportional to ?′(?) and ?′′(?) are neglected as the fringe phase is assumed to be smooth.
In the iteration algorithm, we take the initial guess of ?0(?)=?′(?) and ?0(?)=?′′(?), and in the nth iteration step, we have
When ??(?) and ??(?) are updated, we use a super-Gaussian window of exp?(−??4/?4) in the spatial frequency domain to filter out high-frequency oscillations in ??(?) and ??(?) profiles, where ?? is the reciprocal spatial frequency, ?≈0.28m is the filter window size. The intermediate variables ??(?) and ??(?) are then updated using Eqs. (5) and (6):
We have performed a simulation to justify the iterative reconstruction algorithm. The to-be-tested hologram ?(?) is calculated based on Eq. (4) using known ground truths of ?(?), ?(?), ?(?) (Supplementary Fig. 1a). Then the algorithm is applied to reconstruct ?(?), ?(?), ?(?) from ?(?), and Supplementary Fig. 1b–d shows that the reconstruction results are consistent with the ground truths.
Once ?(?), ?(?) and ?(?) are reconstructed, they are transformed back to the Cartesian coordinate. The spatial intensity ??,?(?,?,?) and phase φ?,?(?)(?,?) can be calculated:
Here, ????(?,?) is the spatial phase of light transmitting through the point-diffraction object (PDO), and can be directly calculated.