Coherent beam combining (CBC) has been employed as a powerful technique to surpass the inherent limitations of a single conventional laser, which has generated significant interest in industrial manufacturing, medical treatments, scientific explorations and other fields in the past decades[1]. More recently, the spotlight has increasingly turned towards the utilization of CBC systems in the generation of structured light[2–9], particularly in scenarios that require higher power and open-environment light manipulation, such as free-space optical communication[10–13]. Significantly, as the scale of the laser array expands, it unlocks greater potential in several key aspects, including enhanced output power, increased editing flexibility and the ability to generate complex structured light with high quality, which paves the way for exploring new frontiers in related optical applications.
High Power Laser Science and Engineering, Volume. 13, Issue 4, 04000e62(2025)
Efficient phase locking in massive laser arrays with deep learning from structured data
Coherent beam combining (CBC) of laser arrays is increasingly attracting attention for generating free-space structured light, unlocking greater potential in aspects such as power scaling, editing flexibility and high-quality light field creation. However, achieving stable phase locking in a CBC system with massive laser channels still remains a great challenge, especially in the presence of heavy phase noise. Here, we propose an efficient phase-locking method for a laser array with more than 1000 channels by leveraging a deep convolutional neural network for the first time. The key insight is that, by elegantly designing the generation strategy of training samples, the learning burden can be dramatically relieved from the structured data, which enables accurate prediction of the phase distribution. We demonstrate our method in a simulated tiled aperture CBC system with dynamic phase noise and extend it to simultaneously generate orbital angular momentum (OAM) beams with a substantial number of OAM modes.
1 Introduction
In a typical CBC system, sub-beams are combined coherently by synchronizing the phase of each individual channel in the laser array, thereby enhancing the combined power[14–16]. Hindered by pernicious random phase noise in CBC systems, particularly exacerbated within high-power configurations, the primary hurdle becomes the rapid and precise detection of phases, which is essential to achieve effective phase locking when the number of channels escalates. With increasing combining scales and output power, conventional phase control methods, such as stochastic parallel gradient descent (SPGD)[17–19], encounter significant challenges in achieving effective phase control, since the speed of phase locking cannot keep pace with phase variation. Chang et al.[20] designed a phase-locking module based on the interferometric technique for a CBC system. However, a reference beam must be integrated and perfectly aligned with the overall setup to ensure proper functionality, thereby adding extra complexity to the system. In recent advances, deep learning (DL) approaches have demonstrated substantial potential in phase prediction and control, attributed to their exceptional capabilities in fast non-iterative forward reasoning, straightforward implementation and potential for scaling up laser arrays[21]. By learning the nonlinear mapping relations between combined far-field intensity patterns and the corresponding phase distributions through a prepared dataset, the network can provide accurate phase predictions from various intensity images. In the last 5 years, many investigations of DL methods have been presented to realize tiled aperture CBC systems[22–31]. In 2019, Hou et al.[22] introduced the supervised learning-based DL method to CBC for the first time. A well-trained convolutional neural network (CNN) VGG-16 was utilized to predict the phase error of the 7-channel and 19-channel CBC systems. Subsequently in 2020, a 12-channel phase-locked system based on two-stage phase control was demonstrated for the generation of vortex beams with orbital angular momentum (OAM), integrating the DL and SPGD methods[6]. In 2021, Wang et al.[27] implemented an 81-channel CBC based on a 9
Although there have been a significant number of studies on DL-based CBC, which is regarded as a potent method for scalability[22], the combined scale is still limited to the order of tens of channels. The upper limit of the number of channels in a laser array that DL-based methods can effectively support is still an open question, on which no consensus has been reached yet. The primary challenge lies in the fact that as the count increases to hundreds or even thousands of channels, accurately learning phase prediction from a single complex pattern image becomes exceedingly difficult[21,22]. The training strategy in previous works would struggle to learn the mapping in such high-dimensional spaces and fail to reach convergence. In addition, there has been limited evaluation of performance under significant dynamic noise, which is critical for performance evaluation on CBC systems.
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
In this study, we demonstrate the achievement of stable phase locking in a simulated tiled aperture CBC system with more than 1000 channels using DL for the first time, to the best of our knowledge. The key observation is that with the random sampling used to generate training data in previous work it is highly difficult for neural networks to learn the inherent mapping between far-field intensity profiles and near-field phase distributions. Instead, we introduce a novel sampling strategy called ‘ladder sampling’, which can create structured training data and dramatically alleviate the learning burden for phase prediction in large-scale laser arrays. We train a ResNet-50 network to estimate the phase distribution from the structured data, and thus to guide the phase control of each beam unit under dynamic noise and make them synchronized. Furthermore, we employ our phase-locking method in a 1000-channel array to simultaneously generate OAM beams with a substantial number of modes (18), highlighting the great potential of our approach for multi-channel OAM multiplexing in free-space optical communications.
2 Methods
Figure 1 illustrates the optical configuration for executing CNN-based phase locking in a 1000-level CBC system, forming the basis for the simulated experiments discussed in this paper. The linearly polarized seed laser (SL) with a wavelength of 1064 nm is amplified by a pre-amplifier (PA) and split into N components via a 1
![]()
Figure 1.Experimental setup for implementing the phase control for CBC based on our deep learning method.
2.1 Design of the CNN
The proposed CNN structure (Figure 2(a)) is based on the ResNet[32] architecture with modifications: the input channels of the initial convolutional layer are reduced from three to one since the input far-field patterns are grayscale intensity profiles. Furthermore, the output layer uses a Tanh activation function to map the outputs within the range of [–1, 1], which limits the output prediction to a particular phase range. The CNN takes a 224
![]()
Figure 2.Details of the constructed CNN. (a) Overview architectures of ResNet-18 and ResNet-50. (b) Bottleneck structure of ResNet-50. (c) Basic block structure of ResNet-18.
In ResNet-50, each stage consists of residual blocks designed as ‘bottlenecks’. A bottleneck (Figure 2(b)) is structured with three layers: a 1
Finally, a global average pooling layer (avgpool) is utilized to condense each unit of the feature map into a single value, followed by an FC layer with Tanh activation to provide the prediction for the current relative phase distribution.
The cost function for our CNN is characterized by the mean-square error (MSE) between the predicted output and the actual label. The MSE for a set of samples is given by the following:where
2.2 Training data collection based on ladder sampling
In a tiled aperture CBC system, the emission unit of the array is typically a linearly polarized fundamental Gaussian beam, and the complex amplitude of the beam array at the source plane is described by the following:where
The coordinates of the observation plane are represented by
The above CBC model is utilized to acquire a sufficient number of training samples. In addition, the parameter settings of our 1027-channel hexagonal CBC system are
Driven by the intrinsic characteristics of the Fourier transform, diverse phase distributions, such as global phase shift and conjugate inversion, can result in identical far-field intensity profiles at the focal plane. This attribute complicates the inverse problem into a one-to-many mapping, which is not appropriate for network training. Consequently, we utilize the phases relative to the central beam, to annotate our dataset, thus removing the influence of global phase shift. In addition, all our far-field patterns are generated at the non-focal plane, situated 0.3 m behind the focal plane, to eliminate the data collision associated with conjugate inversion.
In previous DL-based CBC work, the training data is commonly generated by randomly sampling a phase distribution for the laser arrays. That means the phase of each laser channel is a random value independently sampled from a
To guarantee a training dataset with adequate diversity for training purposes, we introduce a ‘ladder sampling’ strategy designed to arrange phase distributions into multiple designated interval ranges. The patterns generated with our ladder sampling strategy comprehensively span the entire normalized PIB range from 0 to 1, greatly improving the diversity in the dataset. Specifically, by evenly dividing the 2
![]()
Figure 3.(a) Phase distributions of the 20 subsets generated through ladder sampling. Each arc represents a subset. (b)–(d) Non-focal-plane, focal-plane and source-plane visualization in different phase distributions in a 1027-channel laser array. (b1)–(b3) Non-focal plane patterns in the phase ranges of  0.3
0.3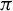 ,
,  0.7
0.7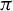 and
and 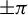 , respectively. (c1)–(c3) The corresponding intensity profiles at the focal plane. (d1)–(d3) The corresponding near-field phase distributions to the above far-field patterns. (e) Comparison of ladder sampling and random sampling strategies.
, respectively. (c1)–(c3) The corresponding intensity profiles at the focal plane. (d1)–(d3) The corresponding near-field phase distributions to the above far-field patterns. (e) Comparison of ladder sampling and random sampling strategies.
3 Results and discussion
3.1 Phase locking of a 1000-channel laser array
We train ResNet-50 with 350,000 samples for phase prediction, and generate another 3500 samples for validation. During training, with a batch size of 32, the parameters of our CNN are iteratively updated by backpropagation using the Adam optimizer, which merges the advantages of AdaGrad and RMSProp to ensure rapid convergence and robust generalization. In addition, a learning rate decay strategy is employed, based on the loss of the validation set, to guide network convergence. In detail, the initial learning rate of 0.0001 will be reduced to 1/10 of itself if the loss of the validation dataset does not decrease over the past five epochs. Our CNN is built using the PyTorch 3.11 library, and the training is executed on a single NVIDIA GeForce RTX 3090 GPU.
After training, we evaluate our phase prediction by employing the dynamic simulation of a 1027-channel CBC system, capable of generating phase noise at extremely high frequencies and dynamically demonstrating the phase-locking mechanism. Starting with a random initial phase distribution, perturbative phase noise is constantly introduced to each beam, characterized by user-specified parameters for frequency and amplitude intervals. The implementation of phase locking is achieved by compensating for the relative phase discrepancies perpetually disrupted by stochastic noise, which requires both precise phase prediction and rapid corrective action. If the response time of phase compensation significantly falls behind the change of dynamic noise, aligning the phase of each component becomes impossible. To improve the speed of forward reasoning of our trained ResNet-50, we adopt cuDNN, a GPU-accelerated library, and TensorRT for FP16 half-precision calculation, which improves the inference of networks on NVIDIA GPUs and significantly reduces the cost of a single-time phase prediction from 6.80 to 0.62 ms.
For systems suffering from dynamic phase noise interference with a frequency of 5000 Hz and a random amplitude range of
![]()
Figure 4.Phase-locking results of the 1027-channel CBC system. (a) Normalized PIB variation of the system with dynamic phase noise in open and closed loops. (b) Phase-locking performances of networks with and without cuDNN and TensorRT accelerations (phase noise: 5000 Hz,  0.2 rad).
0.2 rad).

Table 1. Average normalized PIB of the 1027-channel CBC system with dynamic phase noise of different levels.
Table 1. Average normalized PIB of the 1027-channel CBC system with dynamic phase noise of different levels.
PIB $\pm 0.1\vphantom{A^{A^1}}$ $\pm 0.2$ $\pm 0.3$ $\pm 0.4$ $\pm 0.5$ $\mathrm{Frequency\ (Hz)}$ rad rad rad rad rad 1000 0.997 0.990 0.979 0.963 0.943 2000 0.994 0.979 0.954 0.920 0.878 5000 0.983 0.942 0.870 0.783 0.678
To demonstrate the necessity of employing cuDNN and TensorRT for network acceleration, we evaluate the phase-locking performance under various conditions. As shown in Figure 4(b), without the application of acceleration techniques, the time cost for a single network response on the GPU is 6.8 ms, resulting in a significantly oscillating phase-locking performance averaging 0.49 in the closed-loop configuration. In contrast, the deployment of the network with cuDNN and TensorRT in FP16 half-precision calculating reduces the response time to 0.62 ms. This substantial decrease in response time effectively mitigates the impact of phase noise on the system, thereby achieving a more stable phase-locking performance, with the PIB value improving to approximately 0.94.

Table 3. Time consumption and phase-locking performance of networks under different acceleration strategies (phase noise: 5000 Hz,
 0.2 rad).
0.2 rad).Table 3. Time consumption and phase-locking performance of networks under different acceleration strategies (phase noise: 5000 Hz,
 0.2 rad).
0.2 rad).Acceleration strategies GPU GPU+cuDNN GPU+cuDNN +TensorRT GPU+cuDNN +TensorRT+FP16 Response time (ms) 6.80 5.23 1.48 0.62 Normalized PIB 0.491 0.577 0.862 0.942
To offer further substantial evidence of the advantages of DL techniques in large-scale CBC systems, we evaluate the performance of our approach against the SPGD algorithm in Figure 5, using the phase noise data collected from a real high-power fiber AMP operating under 1 kHz[20]. The configuration of SPGD algorithms is set according to Ref. [17], with a 100 kHz execution speed, a two-sided perturbation at an amplitude of 0.05 rad and a gain coefficient of 180. The evaluation function is calculated as the combined power within half the size of the central main lobe. It is clear that our approach significantly surpasses the SPGD algorithm in terms of phase locking. Specifically, our CNN attains nearly optimal phase locking in 0.01 seconds, featuring an average normalized PIB value of 0.93 in the closed loop. In contrast, the SPGD algorithm struggles with dynamic phase noise, causing the normalized PIB to fluctuate and remain significantly lower, without any notable improvement. In addition, a separate ResNet-50 is trained using the traditional random sampling dataset[6], consisting of a total of 3.5 million training patterns, which is 10 times greater than in ladder sampling. However, the network struggles to achieve convergence during the training stage and performs poorly in the phase-locking test. The phase-locking results indicate that the DL method with the traditional random sampling method completely fails in such a massive CBC system.
![]()
Figure 5.Phase-locking performances of the DL method and SPGD algorithm in the 1027-channel CBC system with dynamic phase noise from real high-power fiber amplifiers.
3.2 Influence of sample generation
To demonstrate the efficacy of our sample generation methodology for training data, we present a comparative analysis of the phase-locking performance of a hexagonal 61-channel CBC system, which is subject to random phase noise of 5000 Hz and
In prior studies on DL-based CBC, the phase profiles of the training samples are conventionally generated through random sampling, whereby the phase of each individual sub-beam is independently and randomly sampled from
We create four groups of datasets for each strategy, with sample numbers of 5000, 10,000, 100,000 and 200,000, respectively. Specifically, the 2
![]()
Figure 6.Phase-locking results of the 61-channel system with dynamic phase noise under different data generation and volume. (a)–(d) PIB variation in a closed loop with ResNet-18 trained on 5000, 10,000, 100,000 and 200,000 samples for each generating strategy, respectively. (e)–(h) PIB distributions of the corresponding training samples for (a)–(d).
Networks trained using ladder sampling exhibit efficient CBC performance, with average normalized PIB values consistently exceeding 0.95. Even with a very small dataset of 5000 samples, our ladder sampling allows the DL method to reach an average PIB of 0.953, while random sampling can only offer an average PIB of 0.12 (Figure 6(a)). Furthermore, for networks trained with random sampling, effective CBC can only be achieved with 200,000 samples, yielding an average PIB of 0.879, still significantly lower than the combining efficiency observed when ladder sampling is applied to a 5000 dataset, which is 40 times smaller. This suggests that models trained on datasets produced by our method exhibit superior generalization capabilities, despite a significantly smaller volume of training data. Moreover, our observations indicate that with our data generation strategy, the variation in combined PIBs between training with 5000 and 200,000 samples is approximately 0.01. Furthermore, even when increasing the training data size from 200,000 to 300,000 samples, the normalized PIB only improves by merely 0.001. These results demonstrate that our data generation method is capable of producing highly diverse far-field patterns with a very limited amount of data, thereby significantly reducing the volume of data for effective network training.
As noted previously, random sampling leads to much missing of patterns associated with higher PIB values. Its effectiveness highly depends on the fortunate occurrence of encountering similar local patterns of higher PIB values within the extensive amount of randomly generated data. Here, we also illustrate this phenomenon in Figures 7(a1)–7(a5) for a brief demonstration in the same 61-channel laser array setting. We maintain a constant phase for a beam subset within a hexagonal region on the emission plane, while the phase outside can vary randomly. As a result, it is evident that the far-field patterns corresponding to the beams within the hexagonal area exhibit a similar structure in a local region of the non-focal plane (Figures 7(b1)–7(b5), highlighted by white rectangles). This suggests a strong correlation between the phase distribution of a subset of laser sources and its corresponding local pattern in the non-focal plane. Thus, the CNN is trained to utilize the local information of these patterns to make accurate predictions regarding the overall phase distribution on the emission plane. In contrast to traditional sampling strategies, which require the network to train on a vast volume of data to generate various local patterns similar to those across larger PIB ranges, our approach significantly reduces the data volume requirement. Specifically, our ladder sampling strategy directly presents different kinds of intensity structure spanning from PIB 0 to 1, enabling efficient extraction of useful and universally valid features. As a result, our sampling demonstrates substantially improved phase-locking performance with a much smaller training dataset compared to conventional methods.
![]()
Figure 7.Local correlation between far-field patterns and near-field phase distributions. (a1)–(a5) Five near-field phase maps containing locally equal phase distributions within the hexagonal areas. (b1)–(b5) The corresponding far-field patterns of (a1)–(a5) with similar intensity profiles in the rectangular areas.
3.3 Influence of the CNN architecture

Table 4. Average normalized PIB of CBC systems with different network structures (phase noise: 5000 Hz,
 0.2 rad).
0.2 rad).Table 4. Average normalized PIB of CBC systems with different network structures (phase noise: 5000 Hz,
 0.2 rad).
0.2 rad).PIB 127 channels 397 channels 1027 channels (10,000 (100,000 (350,000 $\mathrm{Network}$ samples) samples) samples) ResNet–18 0.943 0.962 0.552 ResNet–50 0.047 0.928 0.943
Within the 127-channel system, ResNet-50 does not succeed in achieving phase locking, whereas ResNet-18 attains an average normalized PIB of 0.934. The predominant cause for this disparity is the limited size of the dataset for the given task, in conjunction with the deeper architecture of ResNet-50 relative to ResNet-18. This difference led to overfitting during the training process. Consequently, an increase in the volume of training data is necessary for ResNet-50 to achieve efficient CBC within the 127-element system.
In particular, in the context of the 397-channel system, ResNet-18 exhibits a better combining efficiency compared to ResNet-50. This is attributed to the fact that, on a smaller scale, both networks are sufficiently powerful to execute rational phase prediction after being trained on adequate datasets. However, ResNet-18 comprises fewer layers than ResNet-50, facilitating a faster forward propagation process and thus reducing computational time. In the present experiment, ResNet-18 requires an average of 0.34 ms to complete a single-time phase prediction, while ResNet-50 requires 0.62 ms. Consequently, the expedited response of ResNet-18 diminishes the cumulative phase noise interference to which the system is exposed during a single-time phase modulation, thereby enhancing the system’s combining efficiency compared to that achieved with ResNet-50.
For the 1027-channel system, the results obtained using ResNet-50 indicate that 350,000 samples are sufficient for effective training and superior learning capabilities are demonstrated with more complicated data compared to ResNet-18. Furthermore, even with an increase in the training samples to 500,000 for ResNet-18, the normalized PIB remains within the range of [0.5, 0.6], thus substantiating that it lacks the learning ability in complex situations of the 1027-channel CBC system.
In summary, for smaller combining scales, deeper models usually require more training data to avoid overfitting. When samples are sufficiently diverse, the learning capacity of the chosen network becomes the main factor that influences the phase-locking performance, especially for large-scale combining. Networks with deeper structures usually achieve better performance but with more computational time consumption, which may degrade the efficiency of combining. Therefore, it is crucial to choose a suitable network structure that balances data learning capacity and phase controlling bandwidth according to different combining scales.
3.4 Generation of multi-mode OAMs
Structured light with specific spatial intensity and phase distributions has found widespread applications in various fields, including particle manipulation, optical communication and imaging[3]. Recent studies have indicated that the generation of specific structured light can be achieved by introducing particular phase distributions into CBC systems. This multi-beam combining approach effectively addresses the challenges associated with traditional methods of structured light generation, such as low output power and limited speed in mode switching[33].
However, the number of array beams is a crucial factor that influences the quality of structured beam generation. To generate structured light with rich phase variations and complex structures, it is often necessary to increase the number of source channels in a laser array. For instance, in the case of OAM beams, relevant studies have indicated that to generate a vortex beam with a topological charge of
In this study, our CNN effectively enables phase control over a coherent array consisting of thousands of channels, paving the way for the generation of high-power vortex beams with large topological charges. Furthermore, the nested structure of the multi-layer beam arrays offers an efficient solution for OAM multiplexing in free-space optical communication[11]. Here, we validate the feasibility of a large-scale CBC system in the generation of complex vortex superpositions. Specifically, we employ an array consisting of 1026 beams arranged in 18 circular layers, with each layer containing different topological charges (designated as 1–18, respectively, in Figure 8(a)) encoded as helical phases to generate complex superpositions in the far field (Figure 8(b)). In detail, the innermost layer contains six beams, while the outermost layer comprises 108 beams, which enables the generation of vortex beams with topological charges ranging from –36 to 36 and allows for the flexible implementation of up to 18 modes of OAM multiplexing.
![]()
Figure 8.1000-channel CBC system for multi-mode OAM superpositions. (a) The phase distribution of the laser array. (b) The focal pattern of (a). (c) The variation of far-field mode purities in phase-locked and unlocked states. (d) The comparison of far-field OAM spectra under different states.
To illustrate the importance of phase locking in this application, we present a comparison of the vortex mode purity in the far field under both phase-locked and unlocked states, as demonstrated in Figure 8(c). Mathematically, the mode purity is quantified by the modulus of the overlap integral between the received mode and the ideal mode. It is evident that, in the absence of phase locking, the beam profile at the receiving plane undergoes severe distortion due to dynamic phase noise, ultimately leading to complete dispersion. In contrast, our efficient phase-locking system consistently corrects piston phase errors through the trained CNN, preserving a stable vortex superposition pattern in which the purity of the mode remains consistently at an average of 97.8
Furthermore, the far-field OAM spectra in different states are shown in Figure 8(d). In the ideal state, the OAM spectra are expected to display a progressively increasing trend in intensity, corresponding to the far-field pattern that includes OAM modes with topological charges spanning from 1 to 18. However, without efficient phase locking, the OAM modes responsible for conveying information cannot be generated correctly and become uncontrollable due to continuous noise interference. This means that the generated OAM spectra would follow a randomly fluctuating distribution, even with unexpected messy modes totally outside of the topological charge range from 1 to 18, far away from the pre-designed OAM modes that convey accurate information. In contrast, employing our phase-locking technique can effectively generate OAM modes that are fairly close to the ideal state, thereby guaranteeing accurate encoding for the information to be transmitted.
4 Conclusion
In an effort to answer the question of the number of channels that can be effectively supported by DL-based methodologies in CBC systems, we have successfully implemented phase locking in a laser array comprising over 1000 channels with a deep CNN for the first time. By leveraging the ladder sampling strategy to generate training data and GPU-accelerated technologies, our approach achieves superior performance in phase locking for CBC systems even under heavy dynamic phase noise. The impacts of various sampling strategies for generating training data, along with the evaluation of different neural networks, are analyzed in detail to provide a more comprehensive overview for DL-based CBC systems. In addition, we illustrate that our effective phase-locking approach in a CBC system allows for the generation of multi-mode OAM beams, presenting significant potential for high-power structured light generation.
[1] A. Brignon. Coherent Laser Beam Combining(2013).
[2] J. Bütow, J. Eismann, V. Sharma, D. Brandmüller, P. Banzer. Nat. Photonics, 18, 243(2024).
[3] A. Forbes, M. De Oliveira, M. Dennis. Nat. Photonics, 15, 253(2021).
[4] D. Lin, J. Carpenter, Y. Feng, S. Jain, Y. Jung, Y. Feng, M. Zervas, D. Richardson. Nat. Commun., 11, 3986(2020).
[5] J. Bütow, V. Sharma, D. Brandmüller, J. Eismann, P. Banzer. Commun. Phys., 6, 369(2023).
[6] T. Hou, Y. An, Q. Chang, P. Ma, J. Li, L. Huang, D. Zhi, J. Wu, R. Su, Y. Ma, P. Zhou. Photonics Res., 8, 715(2020).
[7] M. Veinhard, S. Bellanger, L. Daniault, F. Ihsan, J. Bourderionnet, C. Larat, E. Lallier, A. Brignon, J.-C. Chanteloup. Opt. Lett., 46, 25(2020).
[8] T. Yu, H. Xia, W. Xie, G. Xiao, H. Li. Results Phys., 16, 102872(2020).
[9] J. Long, K. Jin, Q. Chen, H. Chang, Q. Chang, Y. Ma, J. Wu, R. Su, P. Ma, P. Zhou. Opt. Lett., 48, 5021(2023).
[10] B. Rouzé, P. Pichon, M. Gay, L. Bramerie, L. Lombard, A. Durécu. Opt. Express, 31, 26552(2023).
[11] B. Shu, Y. Zhang, H. Chang, S. Tang, J. Leng, P. Zhou. Adv. Photonics Nexus, 3, 036003(2024).
[12] V. Billault, S. Leveque, A. Maho, M. Welch, J. Bourderionnet, E. Lallier, M. Sotom, A. Kernec, A. Brignon. Opt. Lett., 48, 3649(2023).
[13] D. J. Geisler, T. M. Yarnall, M. L. Stevens, C. M. Schieler, B. S. Robinson, S. A. Hamilton. Opt. Express, 24, 12661(2016).
[14] T. Y. Fan. IEEE J. Select. Top. Quantum Electron., 11, 567(2005).
[15] B. He, Q. Lou, J. Zhou, J. Dong, Y. Wei, D. Xue, Y. Qi, Z. Su, L. Li, F. Zhang. Opt. Express, 14, 2721(2006).
[16] G. D. Goodno, C. P. Asman, J. Anderegg, S. Brosnan, E. C. Cheung, D. Hammons, H. Injeyan, H. Komine, W. H. Long, M. McClellan, S. J. McNaught, S. Redmond, J. Simpson, R. Sollee, M. Weber, S. B. Weiss, M. Wickham. IEEE J. Select. Top. Quantum Electron., 13, 460(2007).
[17] P. Zhou, Z. Liu, X. Wang, Y. Ma, H. Ma, X. Xu, S. Guo. IEEE J. Select. Top. Quantum Electron., 15, 248(2009).
[18] M. A. Vorontsov, V. P. Sivokon. J. Opt. Soc. Am. A, 15, 2745(1998).
[19] H. Chang, Q. Chang, J. Xi, T. Hou, R. Su, P. Ma, J. Wu, C. Li, M. Jiang, Y. Ma, P. Zhou. Photonics Res., 8, 1943(2020).
[20] Q. Chang, T. Hou, J. Long, Y. Deng, H. Chang, P. Ma, R. Su, Y. Ma, P. Zhou. J. Lightwave Technol., 40, 6542(2022).
[21] M. Jiang, H. Wu, Y. An, T. Hou, Q. Chang, L. Huang, J. Li, R. Su, P. Zhou. PhotoniX, 3, 16(2022).
[22] T. Hou, Y. An, Q. Chang, P. Ma, J. Li, D. Zhi, L. Huang, R. Su, J. Wu, Y. Ma, P. Zhou. High Power Laser Sci. Eng., 7, e59(2019).
[23] Q. Chang, Y. An, T. Hou, R. Su, P. Ma, P. Zhou. Asia Communications and Photonics Conference, M4A(2020).
[24] T. Hou, Y. An, Q. Chang, J. Long, P. Ma, J. Li, P. Zhou. IEEE J. Select. Top. Quantum Electron., 28, 0900110(2022).
[25] X. Li, C. Peng, X. Liang. Opt. Commun., 527, 128928(2023).
[26] B. Mills, J. A. Grant-Jacob, M. Praeger, R. W. Eason, J. Nilsson, M. N. Zervas. Sci. Rep., 12, 5188(2022).
[27] D. Wang, Q. Du, T. Zhou, D. Li, R. Wilcox. Opt. Express, 29, 5694(2021).
[28] J. Zuo, H. Jia, C. Geng, Q. Bao, F. Zou, Z. Li, J. Jiang, F. Li, B. Li, X. Li. J. Lightwave Technol., 40, 3980(2022).
[29] R. Liu, C. Peng, X. Liang, R. Li. Chin. Opt. Lett., 18, 041402(2020).
[30] Q. Du, D. Wang, T. Zhou, A. Gilardi, M. Kiran, B. Mohammed, D. Li, R. Wilcox. Opt. Express, 30, 12639(2022).
[31] D. Wang, Q. Du, T. Zhou, A. Gilardi, M. Kiran, B. Mohammed, D. Li, R. Wilcox. IEEE J. Quantum Electron., 58, 6100309(2022).
[32] K. He, X. Zhang, S. Ren, J. Sun. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 770(2016).
[33] A. Forbes. Laser Photonics Rev., 13, 1900140(2019).
[34] V. P. Aksenov, V. V. Dudorov, V. V. Kolosov. Quantum Electronics, 46, 726(2016).
[35] V. P. Aksenov, V. V. Dudorov, V. V. Kolosov, M. E. Levitsky. Front. Phys., 8, 143(2020).
Get Citation
Copy Citation Text
Haoyu Liu, Jun Li, Kun Jin, Jian Wu, Yanxing Ma, Rongtao Su, Xiaolin Wang, Jinyong Leng, Pu Zhou. Efficient phase locking in massive laser arrays with deep learning from structured data[J]. High Power Laser Science and Engineering, 2025, 13(4): 04000e62
Category: Research Articles
Received: Feb. 7, 2025
Accepted: Jun. 20, 2025
Posted: Jun. 23, 2025
Published Online: Sep. 22, 2025
The Author Email: Jun Li (lijun_gfkd@nudt.edu.cn), Pu Zhou (zhoupu203@163.com)







 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence

