The interaction of a focused high-power laser beam with a target results in the emission of an intense electromagnetic pulse (EMP) in the radio-frequency and microwave bands. In the case of large laser facilities, the electrical intensity of the EMP can exceed 100 kV/m[1,2]. Such EMPs often interfere with electric signals and can be dangerous to electronic devices, but could also be useful for various applications, such as electromagnetic compatibility (EMC) hardening[3,4], biology[5,6] and defence[7,8]. Although laser-driven EMP emission was first observed in the late 1970s[9], the shape of the EMP spectrum – and hence the dominant mechanisms of laser-driven EMP emission – have not yet been satisfactorily explained in all conditions. The potential applications and efforts to explain the mechanism of laser-driven EMP emission have led to a number of experiments at laser facilities around the world, for example, VULCAN[1,2,10,11], ABC[12,13], ECLIPSE[14–18], LMJ-PETAL[19], PHELIX[20], NIF-ARC[21,22] and the Prague Asterix Laser System (PALS)[23–29]. The current state of laser-driven EMP research is summarized in the review paper by Consoli et al.[30].
High Power Laser Science and Engineering, Volume. 13, Issue 4, 04000e57(2025)
Comprehensive characterization of electromagnetic pulses driven by a sub-nanosecond kilojoule laser
The generation of intense radio-frequency and microwave electromagnetic pulses (EMPs) by the interaction of a high-power laser with a target is an interesting phenomenon, the exact mechanisms of which remain inadequately explained. In this paper we present a detailed characterization of the EMP emission at a sub-nanosecond kilojoule laser facility, the Prague Asterix Laser System. The EMPs were detected using a comprehensive set of broadband diagnostics including B-dot and D-dot probes, various antennas, target current and voltage probes and oscilloscopes with 100 and 128 GS/s sampling. Measurements show that the EMP spectrum was strongly dependent on the laser energy: the maximum frequency of the spectrum and the frequency of the spectrum centroid increased with increasing laser beam energy in the signals from all detectors used. The highest observed frequencies exceeded 9 GHz. The amplitude and energy of the detected EMP signals were scaled as a function of laser energy, power and number of emitted electrons.
1 Introduction
In the works presented so far, various mechanisms are proposed to explain the intense and broadband laser-driven EMPs. However, it is generally believed that EMP emission is mainly related to charge separation caused by the escape of hot electrons accelerated by the laser pulse[30]. These hot electrons can produce EMPs directly, both as the low-frequency residue of transition radiation[31–33] and when they strike the chamber wall and excite resonant oscillations. They indirectly cause EMPs by leaving a voltage on the target and drawing a return current from the chamber, which leads to antenna radiation[15,18,30,34–36]. There are other mechanisms, such as circulating plasma currents[37], the photoionization of metallic surfaces and charged particle deposition[38], which may further influence the EMP spectrum.
Regarding the EMP spectrum, several works have related certain components of the EMP spectrum to the eigenfrequencies of the vacuum chamber[10,13,25,27], target stalk[1,18] and other hardware that may affect EMP propagation or cause its resonances[20,30].
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
In this paper, we present the results of extensive EMP experiments at the kilojoule laser system PALS with a pulse duration of approximately
The structure of this paper is as follows. The experimental setup, including a detailed description of the diagnostic methods, is presented in Section 2. Results of the experiment and discussion may be found in Sections 3 and 4, respectively. Conclusions are summarized in Section 5. Further details and characteristics of the experimental equipment used can be found in the appendix.
2 Experimental setup
The experiments were performed on the kilojoule iodine laser at the PALS infrastructure of the Czech Academy of Sciences[39]. The used laser beam had a full aperture with a diameter of 29 cm, a fundamental wavelength of
The diagnostic setup inside (Figure 1(a)) and outside (Figure 1(b)) the vacuum chamber is shown in Figure 1, and the target configurations are shown in Figure 2. The expanding plasma radiation was observed from the radial direction by a four-frame gated X-ray camera based on a pinhole and microchannel plate (MCP) with a gold photocathode, which is sensitive to photon energies in the range from 100 eV to 10 keV. The spatial resolution of this imaging system is about 40
![]()
Figure 1.Simplified schematic top-view of the experimental setup within (a) and outside (b) the vacuum target chamber.
![]()
Figure 2.Schematics of the various copper target configurations used: (a) thick copper block target 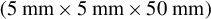 grounded by a massive metal stalk, (b) 1 mm thick rectangular target
grounded by a massive metal stalk, (b) 1 mm thick rectangular target 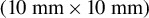 grounded by an inductive current probe and 10 mm copper braid, (c) 1 mm thick rectangular target
grounded by an inductive current probe and 10 mm copper braid, (c) 1 mm thick rectangular target 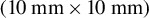 coupled to an inductive current probe and a 50
coupled to an inductive current probe and a 50  coaxial cable and (d) 1 mm thick rectangular target
coaxial cable and (d) 1 mm thick rectangular target 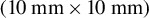 separated from the ground by an insulator with a length of 40 mm and capacity of 6 pF.
separated from the ground by an insulator with a length of 40 mm and capacity of 6 pF.
The target return current caused by the escape of the electrons was measured using an inductive probe[23,42,43] placed between the laser target and the target manipulator. The inductive probe, including the cable used, was tested and calibrated in situ with the help of an electrical pulse generator designed to produce an electrical pulse of a length similar to the laser pulse length at PALS (see the appendix).
As far as the magnetic and electric fields within the chamber are concerned, they were measured by B-dot and D-dot probes, which were shielded by a 2 cm thick polyethylene brick to prevent an influence of charged particles. The B-dot probe (Prodyn Technologies RB-230, 3 dB drop at 5.4 GHz) was placed at a distance of 39 cm from the target, 31° to the laser axis in the horizontal plane and 38° in the vertical plane. The D-dot probe (Prodyn Technologies AD-80, 3 dB drop at
To monitor the EMP outside the vacuum chamber, another identical D-dot probe was placed at a distance of 4.25 m from the target at an angle of
Signals from all of the above-mentioned probes were fed to ultra broadband oscilloscopes (Tektronix DPO73304DX; 100 GS/s sampling, 33 GHz bandwidth and Keysight UXR0104A; 128 GS/s sampling, 10 GHz bandwidth) via cables designed for applications up to 18 GHz (mostly Huber+Suhner S_04272_B, Pasternack PE-P-160LL or equivalents). All cables and accessories were tested using a vector network analyser.
3 Experimental results
3.1 EMPs within the vacuum chamber
In this section, we present results obtained from the EMP diagnostics placed within the vacuum target chamber. A typical B-dot probe signal and retrieved B-field waveform are shown in Figure 3. This exemplary B-dot signal has been obtained in the shot with a laser beam energy of 602 J and a 5 mm thick grounded copper target. In the upper part of Figure 3, there is the visualized B-dot signal in the time base up to 120 ns. The time
![]()
Figure 3.(a) Time-resolved B-dot raw signal from the shot with 5 mm thick copper bar and laser energy of 602 J. The upper graph has a time base of 120 ns, while the lower graph shows a zoomed-in view of the same signal with a 3 ns time range. The points represent the signal samples with a rate of 128 GS/s. (b) Time-resolved waveform of the B-field obtained from the B-dot signal from the same shot as (a).
To see the EMP individual oscillations with a relatively short period of about 200 ps, the identical signal from the same shot but with a zoomed time axis to the 3 ns range is shown in the bottom graphics of Figure 3(a). The black points represent the signal samples with the rate of 128 GS/s. Thanks to the known conversion coefficient of the B-dot probe, it is possible to convert the voltage signal into the values of the magnetic field (see Figure 3(b)). A typical B-field maximum at a distance of 39 cm from the target for the shots with an energy of around 600 J is 0.2–0.4 mT. The dependence of the B-field maximum on the laser energy (Figure 4(a)) and laser peak power (Figure 4(b)) is displayed. As we can see, there is a relatively high variance in the scaling with energy. The reason for this could be the shot-to-shot variation in laser pulse duration, which varies in the range of 250–350 ps in FWHM. The scaling of the B-field maximum with the laser power in Figure 4(b) shows a clearer increasing trend. We can therefore assume that the EMP intensity depends more on the peak power of the laser than on its total energy, at least for lasers with comparable pulse durations. Approximating the EMP as a plane wave travelling in vacuum, the radiated power density is given by
![]()
Figure 4.Intensity scaling of the B-field within the vacuum chamber at a distance 39 cm from the target.
While the increase in the magnetic field intensity maximum with the laser peak power is expected, we also observed a strong dependence of the magnetic field frequency spectrum, which is not easy to explain. The dependence of the B-dot signal spectrum shape on the laser energy is demonstrated in Figure 5. These spectra are obtained by the fast Fourier transform (FFT) of the signals without any correction; only Savitzky–Golay smoothing[44] with a 50 pt window is used for better visualization. In the graph in Figure 5(a) we can see a comparison of the B-dot signal spectra from the shots with the 1 mm thick rectangular copper target at laser energies of 95, 255 and 592 J. Both the upper cut-off frequency and the frequency centroid shift towards higher frequencies as the laser energy increases. Such an effect is even more visible in the case of the shots with the 5 mm thick copper bar target (see Figure 5(b)).
![]()
Figure 5.Comparison of B-dot signal FFT spectra for different target geometries (see Figures 2(a) and 2(b)) for the 5 mm thick target and the 1 mm thick grounded target. For each target geometry the laser energy is varied.
The spectra in Figures 5(a) and 5(b) are not identical because we have significantly changed the geometry of the target and its holder (see Figure 2). Broadening of the spectrum is, however, still clearly visible as the laser energy is increased. The red curve in Figure 5 represents a B-dot FFT spectrum recorded at a laser energy of 152 J. Most of the EMP energy for this shot is carried in the frequency range of approximately 0.5–3 GHz, with the spectrum centroid at about 1.5 GHz. This is typical for laser-driven EMPs[30,34,35].
On increasing the laser beam energy, see the spectrum for 286 J, the spectrum centroid is shifted to approximately 4 GHz, and in the case of the 602 J energy shot, the frequency centroid lies between 5 and 7 GHz, and the highest spectral components reach about 9 GHz – almost the limit of the 10 GHz oscilloscope.
To demonstrate that the broadening of the EMP spectrum with laser energy is reproducible, we present averaged spectra of all the measured B-dot signals from the energy scan in Figure 4. The averaged spectra in Figure 6 are sorted by laser beam energy and peak power – black line: shots with 150–190 J and 0.4–0.7 TW; blue line: shots with approximately 280 J/1 TW; and red line: shots with 500–600 J and 1.6–2.0 TW. Laser shots in the energy scan were taken over several days, so there is some variation in the amplitude of the spectra. However, the shape and bandwidth of the spectra vary consistently with laser energy. We mention that the scaling shot series were performed repeatedly over a few days. Thus, the broadening of the EMP spectrum with the laser power and energy is well reproducible.
![]()
Figure 6.Demonstration of the repeatability by average B-dot signal spectra from a group of shots in terms of energy and peak power – black line: shots with 150–190 J and 0.4–0.7 TW; blue line: shots with approximately 280 J/1 TW; and red line: shots with 500–600 J and 1.6–2.0 TW.
Analogous to the broadening of the magnetic field spectrum, a broadening of the electric field spectrum was observed with the D-dot probe placed at a distance of 41 cm from the target (see Figure 7). These D-dot spectra were obtained in the same shots as the B-dot spectra in Figure 5 with the 1 mm thick rectangle targets (Figure 5(a)) and the 5 mm thick bar targets (Figure 5(b)). As in the case of the B-dot spectra, the D-dot spectra show a reproducible trend with laser energy.
![]()
Figure 7.Comparison of D-dot signal FFT spectra for different target geometries (see Figures 2(a) and 2(b)) for the 5 mm thick target and the 1 mm thick grounded target.
Figure 8 shows the dependence of the electric field maximum on laser peak power for shots with the grounded 5 mm thick copper bar target. Analogous to the magnetic field scaling in Figure 4, here we also observe square root scaling with incident laser power. The bandwidth of EMP measurements is usually limited to a few GHz by cable attenuation or oscilloscope response. Here, we observe EMP signal content up to 10 GHz – higher than that previously recorded[29,30]. Similar to the magnetic field scaling, in Figure 4 we found the square root fit.
![]()
Figure 8.Intensity scaling of the E-field maximum within the vacuum chamber at a distance 41 cm from the target, measured with a D-dot probe.
We mention that the peak intensities from the B-dot and D-dot signals do not match the relation
At the end of this section, we mention that to demonstrate that the broadening of the spectrum is not caused by inappropriate signal processing, all presented spectra are shown without any equalization of the coaxial cable attenuation. Since attenuation increases with frequency, we might expect the highest frequencies to be underestimated.
3.2 EMPs outside the vacuum chamber
An effect of the laser beam energy on the frequency spectrum was also observed in the signals from the EMP diagnostics outside the vacuum chamber, but the effect was not as strong as in the case of the EMP measurement inside the chamber. This may be due to the significantly longer coaxial cable used (10 m long), which results in much higher attenuation at the high frequencies (
Representative frequency spectra of signals from the outer D-dot probe, biconical antenna, vertically polarized horn antenna and horizontally polarized horn antenna from shots with the 5 mm thick copper bar target are shown in Figure 9.
![]()
Figure 9.Comparison of EMP signal spectra detected outside the target chamber.
In the signals of the D-dot probe outside the vacuum chamber, we observed an obvious impact of the laser energy on the electric field spectrum. Looking at Figure 9(a) we can see that the D-dot signal spectrum from the 250 J shot has a centroid at about 2 GHz, whereas at the 602 J shot it has a centroid at approximately 3 GHz. Moreover, the upper frequency cut-off is significantly shifted from approximately 4.5 GHz to approximately 8 GHz.
Even in the signals of the horizontally polarized biconical antenna dedicated to frequencies below 1 GHz, where the observed spectral shift is minimal, we can see a certain increase in the amplitude of peaks at frequencies of 0.9 and 1.1 GHz for the 602 J shot compared to the 154 J shot; see Figure 9(b).
The horn antenna signals are a little more complicated, as shown in Figures 9(c) and 9(d). It is likely that the 10 m coaxial cables mentioned above, which were required to couple the horn antennas to the oscilloscopes in the Faraday cage, attenuate the high-frequency components dependent on the laser energy. The spectral broadening with laser energy appears to be more significant for the horizontally polarized horn antenna (Figure 9(d)) than for the vertically polarized antenna (Figure 9(c)). However, to prove the difference between vertical and horizontal EMP polarization, further experiments with lower attenuation at high frequencies are needed.
3.3 Target current and voltage
The target current was monitored using an inductive probe[23]. The recorded current and its spectrum depend on the geometry of the target and stalk, which act as an electrical filter due to their inductance and capacitance. Due to technical constraints, the closest distance between the point where we monitored the current and the laser focus was 30 mm. In this case, the target was in the form of a copper square with a side length of 10 mm and a thickness of 1 mm mounted on the stalk with a diameter of 2.5 mm. Although multi-GHz frequency components would have been limited by the target geometry and 10 m long coaxial cable, it is still possible to observe a change in the shape of the discharge pulse. Spectral analysis shows a shift of the spectrum centroid and a broadening of the bandwidth with the laser peak power (energy), similar to the case of the EMP signals mentioned above. A comparison of the example inductive probe signals and the target currents obtained by signal integration from a series of shots at different energies is shown in Figure 10.
![]()
Figure 10.Comparison of inductive probe signals from a series of shots at different energies. The left-hand column displays raw signals proportional to the time derivative of the target current, while the right-hand column shows target currents obtained by integrating the probe signals.
In Figure 10, the current pulse shrinks from an FWHM of 520 ps at the 95 J shot to 350 ps at the 576 J shot. This corresponds to a shift in the spectrum centroid from approximately 500 MHz to more than 1 GHz; see the comparison of the target probe signal spectra in Figure 11. Such a broadening of the signal bandwidth is similar to the effect of laser peak power on the spectrum of the B-dot, D-dot and antenna signals shown above.
![]()
Figure 11.Comparison of the FFT spectra of the inductive target current probe signals from shots with different energies.
To visualize more clearly the influence of the laser peak power on the target current, the scaling of the maximum target current and the centre frequency of the spectrum as a function of laser energy is plotted in Figures 12(a) and 12(b), respectively. The measured points in the scaling of the target current maximum were interpolated using the square root of the laser power, as in the case of the B-field and E-field maxima. The square root function also fits well with the laser power dependence of the central frequency.
![]()
Figure 12.Scaling of the target current maximum and spectrum central frequency as a function of the laser peak power.
The results of the target current measurement with the inductive probe were supported by a complementary measurement with the target voltage probe. The geometry of the target and its holder were identical, but instead of being coupled to ground, the target was coupled to a high-voltage attenuator with an input impedance of 50
![]()
Figure 13.(a) Comparison of the target voltage signal obtained from a series of shots at different energies. (b) Scaling of the target voltage maximum with the laser peak power.
Comparing the target voltage and target current waveforms we can see that in both cases the pulse shortens with laser energy, and at energies above 100 J the positive pulse is followed by a negative overshoot, exactly as in the current waveform given by the inductive probe.
As with inductive probe measurements, the shrinking of the target voltage pulse causes the signal bandwidth to widen. Such a dependence is visualized in Figure 14. At the end of this section we should mention that, since both the target current and voltage are not measured directly at the point of laser–plasma interaction, but rather at the end of the target stalk, the shape of the pulses could be somewhat stretched by the target and its stalk inductance and capacitance, which partly act as a low-pass filter. Consequently, the peak current and voltage at the point of laser–plasma interaction could be higher than we measured, but it should not have a significant effect on the total charge given by the time integration of the current, which reaches approximately 400 nC at the energy of approximately 500 J. Also, despite the partial filtering of higher frequencies, we were still able to observe the effect of increasing of the upper cut-off frequency of the signal with increasing laser beam energy.
![]()
Figure 14.Comparison of the target voltage spectra obtained from shots with different energies.
3.4 EMP scaling
As these experiments were carried out using the four configurations described in Section 2 – namely, a copper bar
![]()
Figure 15.Energies of the signals of the EMP detector used as a function of the laser peak power.
Although the laser intensity at focus would be a more reliable scaling parameter than laser peak power, PALS still lacks a diagnostic that would give us information about the laser distribution within the approximately 100
The energy spectrum and angular distribution of the electron emission were monitored by six electron spectrometers at different angles (see Figure 1(a)). These spectrometers can detect the hot electrons with energies above 50 keV and are calibrated using particle tracking simulations[40,41]. An exemplary electron spectrum measured in the shot with the copper bar target (Figure 2(a)) and a peak power of 2.2 TW (energy of 613 J) is shown in Figure 16. Approximating the hot electron spectra in Figure 16 by the single temperature exponential distribution function, as follows:we can find the hot electron temperatures and plot their angular distribution (see Figure 17(a)).
![]()
Figure 16.Exemplary electron spectra from the shot with the copper bar target 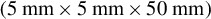 and laser peak power of 2.2 TW (energy of 613 J).
and laser peak power of 2.2 TW (energy of 613 J).
![]()
Figure 17.Angular distribution of electron temperature (a) and fluence (b), and electron fluence as a function of the absolute value of the emission polar angle (c), in the energy range of 50 keV–2 MeV, measured during a shot with a peak power of 2.2 TW (corresponding to an energy of 613 J).
Integrating the electron spectra with respect to energy gives the angular distribution of the electron fluence in the 50 keV–2 MeV energy range:
The distribution of electron fluences evaluated from the exemplary 2.2 TW (613 J) shot is shown in Figure 17(b). As we can see, the electron emission is relatively omnidirectional. In this example shot, the ratio of the highest and lowest detected electron fluence at
To demonstrate the axial symmetry of the electron emission with respect to the laser axis, Figure 17(c) presents the electron fluence as a function of the absolute value of the emission polar angle
The obtained electron numbers were used as a scaling parameter in order to find the relation between the EMP and hot electron emission (see Figure 18). Such scaling of EMP energy with the electron number shows a similar trend to the scaling with peak laser power. The energy of the signal from all detectors increases quite consistently with the electron number and laser peak power, with the exception of the bico nical antenna, where this characteristic appears to be random.
![]()
Figure 18.Energies of the signals of the EMP detector used as a function of the number of emitted electrons.
The random nature of the biconical antenna signal energy with respect to laser peak power and number of emitted hot electrons could be caused by signal distortion due to reflections of electromagnetic waves. Unlike the other EMP detectors, the biconical antenna is more sensitive to lower frequencies in the range of 30 MHz–1 GHz, where standing waves in the laboratory could play a more important role, and its directionality is much less than that of the horn antennas. We therefore plotted the dependence of the amplitude of the first period of the biconical antenna signal oscillations, where we do not expect an influence of reflected waves, in the dependence on the laser peak power (Figure 19(a)) and the electron number (Figure 19(b)) – a parameter that we consider to be directly related to EMP emission. As we can see, the antenna output seems to be proportional to the electron number rather than to the laser peak power. Since the amplitude of the first oscillation seems to be approximately proportional to the number of electrons emitted to the hemisphere in front of the target, it suggests that the random energy content of the biconical antenna signals may have been caused by the frequency-dependent reflection of electromagnetic waves below 1 GHz.
![]()
Figure 19.Amplitude of the first period of the biconical antenna signal in dependence on the laser peak power (a) and number of emitted electrons (b).
4 Discussion
Since our EMP measurements were not performed in an anechoic environment, the detected signals would have been affected by electromagnetic wave reflections and resonances. To determine which frequency components are related to the original laser-driven processes responsible for the EMP emission, or to determine the duration of the original EMP, it is helpful to examine the time evolution of the EMP spectrum. Spectrograms of B-dot, D-dot and horn antenna signals from two 5 mm copper target shots with different energies – 250 J (0.9 TW) and 602 J (2.0 TW) – and a shot with the 1 mm copper target obtained by short-time Fourier transform (STFT) with a 2.3 ns Hanning window are shown in Figure 20. These spectrograms confirm that, consistent with the time-integrated FFT spectra presented in the sections above, the shot with higher energy exhibits a broader spectrum. In addition, the spectra display a distinct time evolution. The spectral components that appear as relatively narrow stripes with constant frequency over time are most likely associated with the eigenfrequencies of the environment or with the EMP-emitting hardware, such as the target stalk conducting the target current. An example of such a stripe is the long-term 1 GHz component observed in the outer D-dot probe and horn antenna signals in both shots. In contrast to these stripes, the prominent regions have a wider bandwidth, with their central frequency not always being constant (see the inner B-dot and D-dot signals in Figure 20). In addition, a relatively sharp boundary can be seen at approximately 5 ns (close to the time resolution given by the STFT window), after which the intensity of these regions is significantly reduced. Although this boundary is visible in all spectrograms in Figure 20, it appears that is more obvious for the detectors outside the chamber and does not change much with the laser peak power. This suggests that the near fields within the chamber exist for longer than the far fields (radiated waves), which could be generated by different mechanisms.
![]()
Figure 20.Spectrograms (STFT) of EMP signals from shots: 250 J and grounded target, 602 J and grounded target and 663 J with insulated target.
The above-mentioned laser power and temporal dependence of the spectrum, as well as the relatively sharp time boundary, indicates that the prominent EMP components originate from processes in the plasma rather than from reflections, which would fade more gradually. It should be noted that even at times much longer than the PALS laser duration (
![]()
Figure 21.Time-resolved plasma expansion in the shot with the laser pulse energy of 506 J and duration of 309 ps taken by the microchannel plate X-ray pinhole camera.
The temporal evolution of the spectrum shape, its strong dependence on the laser beam energy in the signals of all EMPs, target current and target voltage probes indicate that the processes in the laser–plasma and/or the interaction of the emitted charged particles with the strong electric and magnetic fields play a significant role in the EMP emission. A theory that accurately describes the broadening of the EMP spectrum and its evolution over time is still the subject of ongoing research. In the next experiments, we will focus especially on distinguishing the originally emitted EMP from the reflected waves. In addition, we believe that we can increase the bandwidth of EMP measurements outside the chamber, which is limited by cable attenuation due to cable length. An important aspect of further research is laser focus diagnostics, which would help evaluate the focus diameter and, consequently, the laser intensity, and improve the shot-to-shot fluctuation of the results.
5 Conclusion
The systematic experiments performed show that the bandwidth of the EMP increases as the energy of the sub-nanosecond laser beam is increased. This effect was observed in the signals of all EMP detectors, including the target current and target voltage probes. The maximum target currents observed by the inductive probe approached 1.3 kA and the maximum detected voltage to which the target coupled to 50
Using B-dot and D-dot probes within the target chamber, the maximum frequency of the raw signals (without spectral equalization) exceeds 9 GHz at the laser beam energies of about 600 J. Considering the attenuation of the cables used and the limited bandwidth of both the B-dot and D-dot probes, it can be assumed that the higher frequency components of the signals presented are underestimated. The relatively broadband EMP spectrum has a time evolution with a sharp fade at about 5 ns or less, which is visible in the spectrograms.
The signal bandwidth broadening was observed in all target configurations used: a massively grounded 5 mm thick copper bar and
It is generally accepted that laser-driven EMP is not generated by a single mechanism, for example, the target current and its spectrum must be influenced by the eigenfrequencies of the surrounding hardware. The energy-dependent spectral broadening and centroid shift observed in our experiment confirm that other mechanisms may play an important role in EMP production besides antenna emission from the target stalk. Further work is needed to establish whether this is connected to the escaping hot electron distribution, multi-nanosecond evolution of the laser-plasma or some other processes.
Appendix A: Inductive target current probe
The inductive target probe is based on the principle presented in Ref. [
![]()
Figure 22.Testing of the inductive target current probe using an electrical pulse generator.
Appendix B: High-voltage target voltage probe
The high-voltage divider that was used for the measurement of the target voltage was tested using a vector network analyser. The dependence of the attenuation on the frequency is shown in
![]()
Figure 23.Frequency characteristic of the high-voltage target voltage probe.
Appendix C: Horn antennas
In the experiments presented in this paper two linearly polarized double-ridged horn antennas were used: Rohde & Schwarz HF-906 and HF-907, designed for EMC measurements. Such an antenna is schematically visualized in
![]()
Figure 24.Schematic visualization of the double-ridged horn antenna.
![]()
Figure 25.Typical gain of the double-ridged horn antennas, Rohde & Schwarz HF-906 and HF-907, given by the manufacturer.
![]()
Figure 26.In situ cross-calibration of horn antennas HF-906 and HF-907: comparison of signals in the time domain (a) and frequency domain (b).
Appendix D: Frequency responses of cables
In the experiments presented in this paper, we used several kinds of cables: the PE P160LL cable[
![]()
Figure 27.Specific attenuation of the coaxial cables.
[1] P. Bradford, N. C. Woolsey, G. G. Scott, G. Liao, H. Liu, Y. Zhang, B. Zhu, C. Armstrong, S. Astbury, C. Brenner, P. Brummitt, F. Consoli, I. East, R. Gray, D. Haddock, P. Huggard, P. J. R. Jones, E. Montgomery, I. Musgrave, P. Oliveira, D. R. Rusby, C. Spindloe, B. Summers, E. Zemaityte, Z. Zhang, Y. Li, P. McKenna, D. Neely. High Power Laser Sci. Eng., 6, e21(2018).
[2] F. Consoli, R. De Angelis, T. S. Robinson, S. Giltrap, G. S. Hicks, E. J. Ditter, O. C. Ettlinger, Z. Najmudin, M. Notley, R. A. Smith. Sci. Rep., 9, 8551(2019).
[3] F. Sabath, A. Wraight, A. Brenner, C. C. JonesIEEE International Symposium on Electromagnetic Compatibility. , , , and , in 2007 (), p. ., 1(2007).
[4] V. Pereira, G. R. KunkolienkarFourth International Conference on Computing, Communications and Networking Technologies (ICCCNT). and , in 2013 (), p. 1.(2013).
[5] K. H. Schoenbach, S. J. Hargrave, R. P. Joshi, J. F. Kolb, R. Nuccitelli, C. Osgood, A. Pakhomov, M. Stacey, R. J. Swanson, J. A. White, S. Xiao, J. Zhang, S. J. Beebe, P. F. Blackmore, E. S. Buescher. IEEE Trans. Dielectr. Electr. Insulat., 14, 1088(2007).
[6] P. Shaw, N. Kumar, S. Mumtaz, J. S. Lim, J. H. Jang, D. Kim, B. D. Sahu, A. Bogaerts, E. H. Choi. Sci. Rep., 11, 14003(2021).
[7] D. Wang, Y. Li, P. Dehghanian, S. WangNorth American Power Symposium (NAPS). , , , and , in 2019 (), p. 1.(2019).
[8] S.-H. Min, H. Jung, O. Kwon, M. Sattorov, S. Kim, S.-H. Park, D. Hong, S. Kim, C. Park, B. H. Hong, I. Cho, S. Ma, M. Kim, Y. J. Yoo, S. Y. Park, G.-S. Park. IEEE Access, 9, 136775(2021).
[9] J. S. Pearlman, G. H. Dahlbacka. J. Appl. Phys., 49, 457(1978).
[10] M. J. Mead, D. Neely, J. Gauoin, R. Heathcote, P. Patel. Rev. Sci. Instrum., 75, 4225(2004).
[11] T. S. Robinson, F. Consoli, S. Giltrap, S. J. Eardley, G. S. Hicks, E. J. Ditter, O. Ettlinger, N. H. Stuart, M. Notley, R. De Angelis, Z. Najmudin, R. A. Smith. Sci. Rep., 7, 983(2017).
[12] F. Consoli, R. De Angelis, P. Andreoli, M. Cipriani, G. Cristofari, G. Di Giorgio, F. Ingenito2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC). , , , , , , and , in (), p. ., 182(2015).
[13] F. Consoli, R. De Angelis, P. Andreoli, G. Cristofari, G. Di Giorgioa. , , , , and , Phys. Procedia , 11 (2015)..
[14] J.-L. Dubois, F. Lubrano-Lavaderci, D. Raffestin, J. Ribolzi, J. Gazave, A. C. L. Fontaine, E. d’Humières, S. Hulin, P. Nicola, A. Poyé, V. T. Tikhonchuk. Phys. Rev. E, 89, 013102(2014).
[15] A. Poyé, S. Hulin, M. Bailly-Grandvaux, J.-L. Dubois, J. Ribolzi, D. Raffestin, M. Bardon, F. Lubrano-Lavaderci, E. D’Humières, J. J. Santos, P. Nicola, V. Tikhonchuk. Phys. Rev. E, 043106(2015).
[16] A. Poyé, S. Hulin, J. Ribolzi, M. Bailly-Grandvaux, F. Lubrano-Lavaderci, M. Bardon, D. Raffestin, J. J. Santos, V. Tikhonchuk. Phys. Rev. E, 98, 033201(2018).
[17] P. Raczka, J.-L. Dubois, S. Hulin, V. Tikhonchuk, M. Rosinski, A. Zaras-Szydlowska, J. Badziak. Laser Particle Beams, 35, 677(2017).
[18] D. F. G. Minenna, A. Poyé, P. Bradford, N. Woolsey, V. T. Tikhonchuk. Phys. Plasmas, 27, 063102(2020).
[19] M. Bardon, B. Etchessahar, F. Lubrano, S. Bazzoli, M. Ferri, J. Ribolzi, P. Mirabel, A. Compant La Fontaine, N. Mallejac, S. Cadra, L. Chaigne, S. Depierreux, J. Baggio, N. Blanchot, G. Birindelli, A. Casner, V. T. Tikhonchuk. Phys. Rev. Res., 2, 033502(2020).
[20] M. Scisciò, F. Consoli, M. Salvadori, N. E. Andreev, N. G. Borisenko, S. Zähter, O. Rosmej. High Power Laser Sci. Eng., 9, e64(2021).
[21] C. G. Brown, A. Throop, D. Eder, J. Kimbrough. J. Phys.: Conf. Ser., 112, 032025(2008).
[22] C. G. Brown, E. Bond, T. Clancy, S. Dangi, D. C. Eder, W. Ferguson, J. Kimbrough, A. Throop. J. Phys.: Conf. Ser., 244, 032001(2010).
[23] J. Cikhardt, J. Krasa, M. De Marco, M. Pfeifer, A. Velyhan, E. Krousky, B. Cikhardtova, D. Klir, K. Rezac, J. Ullschmied, J. Skala, P. Kubes, J. Kravarik. Rev. Sci. Instrum., 85, 103507(2014).
[24] J. Krása, M. D. Marco, J. Cikhardt, M. Pfeifer, A. Velyhan, D. Klír, K. Řezáč, J. Limpouch, E. Krouský, J. Dostál, J. Ullschmied, R. Dudžák. Plasma Phys. Control. Fusion, 59, 065007(2017).
[25] F. Consoli, R. D. Angelis, M. D. Marco, J. Krasa, J. Cikhardt, M. Pfeifer, D. Margarone, D. Klir, R. Dudzak. Plasma Phys. Control. Fusion, 60, 105006(2018).
[26] M. D. Marco, M. Pfeifer, E. Krousky, J. Krasa, J. Cikhardt, D. Klir, V. Nassisi. J. Phys.: Conf. Ser., 508, 012007(2014).
[27] M. D. Marco, J. Krása, J. Cikhardt, M. Pfeifer, E. Krouský, D. Margarone, H. Ahmed, M. Borghesi, S. Kar, L. Giuffrida, R. Vrana, A. Velyhan, J. Limpouch, G. Korn, S. Weber, L. Velardi, D. D. Side, V. Nassisi, J. Ullschmied. J. Instrum., 11, C06004(2016).
[28] M. De Marco, J. Krasa, J. Cikhardt, A. Velyhan, M. Pfeifer, R. Dudzak, J. Dostal, E. Krousky, J. Limpouch, T. Pisarczyk, Z. Kalinowska, T. Chodukowski, J. Ullschmied, L. Giuffrida, D. Chatain, J.-P. Perin, D. Margarone. Phys. Plasmas, 24, 083103(2017).
[29] P. Raczka, J. Cikhardt, M. Pfeifer, J. Krasa, M. Krupka, T. Burian, M. Krus, T. Pisarczyk, J. Dostal, R. Dudzak, J. Badziak. Plasma Physics Control. Fusion, 63, 085015(2021).
[30] F. Consoli, V. T. Tikhonchuk, M. Bardon, P. Bradford, D. C. Carroll, J. Cikhardt, M. Cipriani, R. J. Clarke, T. Cowan, C. N. Danson, R. De Angelis, M. De Marco, J.-L. Dubois, B. Etchessahar, A. L. Garcia, D. I. Hillier, A. Honsa, W. Jiang, V. Kmetik, J. Krása, Y. Li, F. Lubrano, P. McKenna, J. Metzkes-Ng, A. Poyé, I. Prencipe, P. Rączka, R. A. Smith, R. Vrana, N. C. Woolsey, E. Zemaityte, Y. Zhang, Z. Zhang, B. Zielbauer, D. Neely. High Power Laser Sci. Eng., 8, e22(2020).
[31] G.-Q. Liao, H. Liu, G. G. Scott, Y.-H. Zhang, B.-J. Zhu, Z. Zhang, Y.-T. Li, C. Armstrong, E. Zemaityte, P. Bradford, D. R. Rusby, D. Neely, P. G. Huggard, P. McKenna, C. M. Brenner, N. C. Woolsey, W.-M. Wang, Z.-M. Sheng, J. Zhang. Phys. Rev. X, 10, 031062(2020).
[32] E. Denoual, L. Bergé, X. Davoine, L. Gremillet. Phys. Rev. E, 108, 065211(2023).
[33] S. Herzer, A. Woldegeorgis, J. Polz, A. Reinhard, M. Almassarani, B. Beleites, F. Ronneberger, R. Grosse, G. G. Paulus, U. Hübner, T. May, A. Gopal. New J. Phys., 20, 063019(2018).
[34] Z.-Y. Chen, J.-F. Li, Y. Yu, J.-X. Wang, X.-Y. Li, Q.-X. Peng, W.-J. Zhu. Phys. Plasmas, 19, 113116(2012).
[35] Y. Xia, F. Zhang, H. Cai, W. Zhou, C. Tian, B. Zhang, D. Liu, T. Yi, Y. Xu, F. Wang, T. Li, S. Zhu. Matter Radiat. Extremes, 5, 017401(2020).
[36] K. Nelissen, M. Liszi, M. De Marco, V. Ospina, I. Drotar, G. Gatti, C. Kamperidis, L. Volpe. Sci. Rep., 10, 3108(2020).
[37] F. S. Felber. Appl. Phys. Lett., 86, 231501(2005).
[38] F. Consoli, P. L. Andreoli, M. Cipriani, G. Cristofari, R. De Angelis, G. Di Giorgio, L. Duvillaret, J. Krása, D. Neely, M. Salvadori, M. Scisciò, R. A. Smith, V. T. Tikhonchuk. Philos. Trans. Roy. Soc. A Math. Phys. Eng. Sci., 379, 20200022(2021).
[39] K. Jungwirth, A. Cejnarova, L. Juha, B. Kralikova, J. Krasa, E. Krousky, P. Krupickova, L. Laska, K. Masek, T. Mocek, M. Pfeifer, A. Präg, O. Renner, K. Rohlena, B. Rus, J. Skala, P. Straka, J. Ullschmied. Phys. Plasmas, 8, 2495(2001).
[40] M. Krupka, J. Krasa, R. Dudzak, J. Cikhardt, M. Kalal, T. Burian, D. Klir, K. Rezac, J. Dostal, M. Pfeifer, T. Pisarczyk, T. Chodukowski, Z. Rusiniak. J. Instrum., 14, C12003(2019).
[41] M. Krupka, S. Singh, T. Pisarczyk, J. Dostal, M. Kalal, J. Krasa, R. Dudzak, T. Burian, S. Jelinek, T. Chodukowski, Z. Rusiniak, M. Krus, L. Juha. Rev. Sci. Instrum., 92, 023514(2021).
[42] M. Ehret, J. Cikhardt, P. W. Bradford, I.-M. Vladisavlevici, T. Burian, D. de Luis, J. L. Henares, R. H. Martin, J. I. Apinaniz, R. Lera, J. A. Perez-Hernandez, J. J. Santos, G. Gatti. High Power Laser Sci. Eng., 12, e33(2024).
[43] M. Ehret, I.-M. Vladisavlevici, P. W. Bradford, J. Cikhardt, E. Filippov, J. L. Henares, R. H. Martin, D. de Luis, J. A. Perez-Hernandez, P. Vicente, T. Burian, E. Garcia-Garcia, J. Hernandez, C. Mendez, M. O. Ruiz, O. Varela, M. D. R. Frias, J. J. Santos, G. Gatti. Matter Radiat. Extremes, 10, 027203(2025).
[44] A. Savitzky, M. J. E. Golay. Anal. Chem., 36, 1627(1964).
[45] T. Pisarczyk, S. Y. Gus’kov, T. Chodukowski, R. Dudzak, P. Korneev, N. N. Demchenko, Z. Kalinowska, J. Dostal, A. Zaras-Szydlowska, S. Borodziuk, L. Juha, J. Cikhardt, J. Krasa, D. Klir, B. Cikhardtova, P. Kubes, E. Krousky, M. Krus, J. Ullschmied, K. Jungwirth, J. Hrebicek, T. Medrik, J. Golasowski, M. Pfeifer, O. Renner, S. Singh, S. Kar, H. Ahmed, J. Skala, P. Pisarczyk. Phys. Plasmas, 24, 102711(2017).
[46] T. Pisarczyk, M. Kalal, S. Y. Gus’kov, D. Batani, O. Renner, J. Santos, R. Dudzak, A. Zaras-Szydłowska, T. Chodukowski, Z. Rusiniak, J. Dostal, J. Krasa, M. Krupka, I. Kochetkov, S. Singh, J. Cikhardt, T. Burian, M. Krus, M. Pfeifer, G. Cristoforetti, L. A. Gizzi, F. Baffigi, L. Antonelli, N. N. Demchenko, M. Rosinski, D. Terwińska, S. Borodziuk, P. Kubes, M. Ehret, L. Juha, J. Skala, P. Korneev. Plasma Phys. Control. Fusion, 62, 115020(2020).
Get Citation
Copy Citation Text
Jakub Cikhardt, Philip W. Bradford, Michael Ehret, Shubham Agarwal, Massimo Alonzo, Pierluigi Andreoli, Michal Cervenak, Vittorio Ciardiello, Fabrizio Consoli, Daniele Davino, Jan Dostal, Roman Dudzak, Daniel Klir, Josef Krasa, Michal Krupka, Pavel Kubes, Jakub Malir, Cruz Mendez, Vojtech Munzar, Jan Novotny, Oldrich Renner, Karel Rezac, Marta O. Ruiz, João J. Santos, Massimiliano Sciscio, Sushil Singh, Zuzana Valdova, Libor Juha, Miroslav Krus. Comprehensive characterization of electromagnetic pulses driven by a sub-nanosecond kilojoule laser[J]. High Power Laser Science and Engineering, 2025, 13(4): 04000e57
Category: Research Articles
Received: Feb. 18, 2025
Accepted: May. 15, 2025
Published Online: Sep. 4, 2025
The Author Email:







 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence

