Three-dimensional (3D) measurement has been widely used in the fields of medicine, chemical, engineering, and mechanical design[
Chinese Optics Letters, Volume. 20, Issue 11, 112601(2022)
High-speed three-dimensional shape measurement with inner shifting-phase fringe projection profilometry On the Cover

Fringe projection profilometry (FPP) has been extensively studied in the field of three-dimensional (3D) measurement. Although FPP always uses high-frequency fringes to ensure high measurement accuracy, too many patterns are projected to unwrap the phase, which affects the speed of 3D reconstruction. We propose a high-speed 3D shape measurement method using only three high-frequency inner shifting-phase patterns (70 periods), which satisfies both high precision and high measuring speed requirements. Besides, our proposed method obtains the wrapped phase and the fringe order simultaneously without any other information and constraints. The proposed method has successfully reconstructed moving objects with high speed at the camera’s full frame rate (1700 frames per second).
1. Introduction
Generally, phase unwrapping is classified into spatial phase unwrapping (SPU) and temporal phase unwrapping (TPU) categories[
To overcome the defects of these two traditional methods, numerous phase unwrapping algorithms have been developed. A series of phase-coding methods are proposed by embedding the information of the fringe order into fringe patterns to determine the corresponding fringe order[
Sign up for Chinese Optics Letters TOC Get the latest issue of Advanced Photonics delivered right to you!Sign up now
We propose a high-precision, high-speed 3D shape measurement method using only three inner shifting-phase patterns to acquire the 3D shape of measured objects. In this method, we encode the phase and the corresponding fringe order information into these three patterns. Thus, the wrapped phase and fringe order are obtained simultaneously without any additional patterns to unwrap the phase. Besides, it can suppress the influence of ambient light and noise well by encoding in the phase domain. Because only three patterns are projected, the proposed method can be applied in high-speed measurement fields. The experimental results demonstrate the stability and effectiveness of the proposed method. Furthermore, a high-speed measurement system is prepared to reconstruct moving objects at the camera’s full frame rate (1700 frames per second). The method of inner shifting-phase fringe projection was first proposed in our previous work [28,29], which required four patterns. In this paper, we reduced the number of patterns to three, which should achieve higher efficiency with fewer pictures.
2. Principle of the Method
We set up three patterns to achieve the wrapped phase and fringe order simultaneously by embedding the phase and fringe order information into the phase domain. These three projected patterns are shown in Fig. 1.
![]()
Figure 1.Three projected patterns. (a)–(c) Three projected fringe patterns. (d)–(f) One section of the three patterns.
Three patterns are expressed as follows:
The wrapped phase and the shifting phase are calculated by Eqs. (1) to (3) as follows:
The range of the wrapped phase is from 0 to in one period, and the range of the shifting-phase is from 0 to . is an unknown number, and we obtain its value with the same method in Ref. [36]. Equations (8) and (9) are the key steps to get Eq. (7). Since the wrapped phase is a curve with T periods, we use the single-frequency shifting phase to get the fringe order for each cycle of the wrapped phase:
![]()
Figure 2.Detail of finding k.
From the wrapped phase and fringe order, we get the absolute phase as follows:
The procedure of our method is shown in Fig. 3.
![]()
Figure 3.Procedure of the method. (a) One projected pattern. (b) The wrapped phase. (c) Map of A. (d) The shifting phase. (e) The absolute phase. (f) The 3D reconstruction result.
The procedure of the proposed method can be listed as four steps.
Procedure 1: we achieve the wrapped phase by Eq. (6) and get the value of A with the method in Ref. [36] from the captured patterns.
Procedure 2: we obtain the shifting phase by Eq. (7) from the captured patterns and the value of A.
Procedure 3: we calculate the fringe order by Eq. (10) and calculate the absolute phase by Eq. (11) from the wrapped phase and fringe order.
Procedure 4: we retrieve the 3D reconstruction result by the absolute phase and calibration result.
3. Experiments
In order to verify the performance of the proposed method, we set a high-speed FPP system, which includes a computer, an image grabbing card (Active Silicon CoaXPress-AS-FBD-4XCXP6-2PE8), a high-speed CMOS camera (Vision Research Phantom S210, resolution, full frame: 1700 frames per second), and a high-speed digital light processing (DLP) projection system. The high-speed DLP projection system consists of a DLP development kit (Texas Instruments DLP Discovery 4500) and a wide extended graphics array (WXGA) resolution () digital micromirror device (DMD). On the basis of binary defocus technology, our projector can reach up to 4250 frames per second. The camera and the projector system are shown in the Fig. 4. In these experiments, we generated three high-frequency patterns with 70 fringe periods.
![]()
Figure 4.Measurement system.
Section 1: we conducted an experiment to verify the accuracy of our method. In this experiment, we employed two methods to measure two standard ceramic spheres whose diameter is 50.805 mm, and distance between sphere centers (L) is 100.035 mm, based on manufacturing specification and precision. These two methods include the traditional method (three-frequency three-step algorithm)[

Table 1. Comparisons of the Two Methods
Table 1. Comparisons of the Two Methods
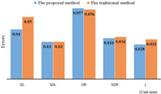
![]()
Figure 5.Two ceramic spheres. (a) One of the three captured patterns. (b) Wrapped phase map. (c) The 3D reconstruction result of two ceramic spheres.
![]()
Figure 6.Schematic diagram of measuring distance between sphere centers (L) and diameter of reconstruction results.
![]()
Figure 7.Six different angles.
Section 2: we measured a cartoon mask to demonstrate the capability of absolute phase recovery of the proposed method. Figure 8(a) represents one of the three captured patterns of the cartoon mask. Figure 8(b) is the wrapped phase map of the cartoon mask. One cross section of the wrapped phase and its counterpart of the reference phase are plotted in Fig. 8(d). As shown in Fig. 8(c), a great 3D reconstruction result is achieved, proving the proposed method’s stability and robustness in measuring the complex object.
![]()
Figure 8.One cartoon mask. (a) One of the three captured patterns. (b) Wrapped phase map of the cartoon mask. (c) The 3D reconstruction result of the cartoon mask. (d) One cross section of the wrapped phase and its counterpart of the reference phase in (a).
Section 3: the ability of calculating the wrapped phase and the fringe order pixel-to-pixel of our method can be proved by measuring isolated objects. We arranged an experiment to measure two sculptures (‘crab’ and ‘rabbit’) positioned on a black cloth background, as shown in Fig. 9(a). The black cloth completely separates the pixel points between the two sculptures. Figure 9(b) shows the wrapped phase of the two sculptures. One cross section of the wrapped phase and its counterpart of the reference phase are plotted in Fig. 9(d). The correct depth and good reconstruction results, as shown in Fig. 9(c), prove the feasibility of our method in measuring isolated objects.
![]()
Figure 9.Two isolated sculptures. (a) One of the three captured patterns. (b) Wrapped phase map of two isolated sculptures. (c) The 3D reconstruction result of two isolated sculptures. (d) One cross section of the wrapped phase and its counterpart of the reference phase in (a).
Section 4: after confirming 3D measurement capability of the complex surface and the isolated objects, the proposed method can be widely used to measure colorful objects with varying textures in this subsection. Thus, we performed an experiment to measure a colorful ‘tortoise’ sculpture, as shown in Fig. 10(a). Figure 10(b) shows the wrapped phase map of this sculpture. One cross section of the wrapped phase and its counterpart of the reference phase are plotted in Fig. 10(c). Figure 10(d) shows the 3D reconstruction result of this colorful sculpture. Furthermore, we added the RGB information into the 3D reconstruction of this sculpture. Then, a colorful 3D reconstruction is obtained, as shown in Fig. 10(e). This experiment demonstrates that the proposed method reconstructs the colorful object well.
![]()
Figure 10.One colorful sculpture. (a) One of the three captured patterns. (b) Wrapped phase map of the colorful sculpture. (c) One cross section of the wrapped phase and its counterpart of the reference phase in (a). (d) The 3D reconstruction result of the colorful sculpture. (e) Colorful 3D reconstruction result.
Section 5: a high-speed 3D measurement of the moving object (paper airplane with wings vibrating in the wind) is performed by our system. Since the proposed method uses three patterns to achieve the absolute phase map, we set the speed to the camera’s full frame rate (1700 frames per second) in this high-speed 3D measurement. The reconstruction speed of a moving object with the proposed method is 1700 frames per second, which is the camera’s full frame rate. For any frame of picture, the previous frame and the next frame are used to calculate the phase. In this way, we can get 3D information for each frame of the picture, as shown in Fig. 11. Figure 12(a) shows the paper airplane and the dynamics of the aircraft vibration. Figures 12(b) and 12(c) show one of the frames in the dynamic process (the collected picture and the reconstruction result). The wings of an airplane vibrate in the wind at a high frequency, and the amplitude of the vibration is within 20 mm, which shows that the small rapid vibration can be accurately captured and reconstructed by our method. We extract the corners (P1, P2, P3) shown in Fig. 12(c) of the paper airplane to show its vibration displacement (D) and frequency in the Z direction shown in Fig. 13. The whole 3D reconstruction process can be referred to in
![]()
Figure 11.Principle of getting full frame rate.
![]()
Figure 12.Paper airplane with wings vibrating in the wind.
![]()
Figure 13.Vibration track of the airplane.
Section 6: in the last experiment, we employed our system to measure the moving object (the fingers reciprocated in front of the camera) again. Pictures in the left of Figs. 14(a)–14(d) are representative camera images, and pictures in the right of Figs. 14(a)–14(d) are corresponding 3D reconstruction results at different frame points. We show the gestures of the fingers in different four frames (frame 44, frame 485, frame 1167, frame 1685). From the effect of the pictures below, we get good reconstruction results. A more detailed comparison of the original motion and reconstruction results is provided in
![]()
Figure 14.Moving hand. (a)–(d) show 2D captured patterns in the left and corresponding 3D reconstruction results in the right at the point frame 44, frame 485, frame 1167, and frame 1685.
4. Conclusion
A novel high-speed 3D shape measurement for moving objects has been presented. Since only three inner shifting-phase patterns are used to acquire the wrapped phase and the fringe order simultaneously, it meets the requirements of high-speed and full-field. The number of periods of projected patterns reaches 70, ensuring the accuracy. The experiments discussed above have confirmed the ability to measure complex, colorful, and isolated objects. Moreover, the high-speed 3D measurement experiment for moving objects at 1700 frames per second has also demonstrated its capability for high speed, high robustness, no geometry constraint, and full-field 3D shape acquisition.
[1] Y. An, J. S. Hyun, S. Zhang. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system. Opt. Express, 24, 18445(2016).
[2] S. Xing, H. Guo. Correction of projector nonlinearity in multi-frequency phase-shifting fringe projection profilometry. Opt. Express, 26, 16277(2018).
[3] K.-C. C. Chien, H.-Y. Tu, C.-H. Hsieh, C.-J. Cheng, C.-Y. Chang. Regional fringe analysis for improving depth measurement in phase-shifting fringe projection profilometry. Meas. Sci. Technol., 29, 015007(2018).
[4] C. Zuo, S. Feng, L. Huang, T. Tao, W. Yin, Q. Chen. Phase shifting algorithms for fringe projection profilometry: a review. Opt. Lasers Eng., 109, 23(2018).
[5] S. Yu, J. Zhang, X. Yu, X. Sun, H. Wu, X. Liu. 3D measurement using combined Gray code and dual-frequency phase-shifting approach. Opt. Commun., 413, 283(2018).
[6] M. Servin, M. Padilla, G. Garnica. Super-sensitive two-wavelength fringe projection profilometry with 2-sensitivities temporal unwrapping. Opt. Lasers Eng., 106, 68(2018).
[7] Y. Liu, Q. Zhang, H. Zhang, Z. Wu, W. Chen. Improve temporal Fourier transform profilometry for complex dynamic three-dimensional shape measurement. Sensors, 20, 1808(2020).
[8] X. Liu, J. Kofman. Real-time 3D surface-shape measurement using background-modulated modified Fourier transform profilometry with geometry-constraint. Opt. Lasers Eng., 115, 217(2019).
[9] H. Zhang, Q. Zhang, Y. Li, Y. Liu. High speed 3D shape measurement with temporal Fourier transform profilometry. Appl. Sci., 9, 4123(2019).
[10] D. Zheng, Q. Kemao, J. Han, J. Wang, H. Yu, L. Bai. High-speed phase-shifting profilometry under fluorescent light. Opt Lasers Eng., 128, 106033(2020).
[11] J. Zhang, Y. Zhang, B. Chen, B. Dai. Full-field phase error analysis and compensation for nonsinusoidal waveforms in phase shifting profilometry with projector defocusing. Opt. Commun., 430, 467(2019).
[12] J. S. Hyun, S. Zhang. Enhanced two-frequency phase-shifting method. Appl. Opt., 55, 4395(2016).
[13] Y. Xu, S. Jia, Q. Bao, H. Chen, J. Yang. Recovery of absolute height from wrapped phase maps for fringe projection profilometry. Opt. Express, 22, 16819(2014).
[14] Q. Zhang, Y. Han, Y. Wu. Comparison and combination of three spatial phase unwrapping algorithms. Opt. Rev., 26, 380(2019).
[15] G. Dardikman, G. Singh, N. T. Shaked. Four dimensional phase unwrapping of dynamic objects in digital holography. Opt. Express, 26, 3772(2018).
[16] S. Lian, H. Kudo. Improved algorithm for phase unwrapping with continuous submodular minimization. 3rd International Conference on Vision, Image and Signal Processing(2019).
[17] C. Zuo, L. Huang, M. Zhang, Q. Chen, A. Asundi. Temporal phase unwrapping algorithms for fringe projection profilometry: a comparative review. Opt. Lasers Eng., 85, 84(2016).
[18] M. Gdeisat. Performance evaluation and acceleration of Flynn phase unwrapping algorithm using wraps reduction algorithms. Opt. Lasers Eng., 110, 172(2018).
[19] L. Li, Y. Zheng, K. Yang, X. Su, Y. Wang, X. Chen, Y. Wang, B. Li. Modified three-wavelength phase unwrapping algorithm for dynamic three-dimensional shape measurement. Opt. Commun., 480, 126409(2020).
[20] X. He, Q. Kemao. A comparison of n-ary simple code and n-ary Gray code phase unwrapping in high-speed fringe projection profilometry. Opt. Lasers Eng., 128, 106046(2020).
[21] X. He, D. Zheng, Q. Kemao, G. Christopoulos. Quaternary Gray-code phase unwrapping for binary fringe projection profilometry. Opt. Lasers Eng., 121, 358(2019).
[22] Q. Zhang, X. Su, L. Xiang, X. Sun. 3-D shape measurement based on complementary Gray-code light. Opt. Lasers Eng., 50, 574(2012).
[23] F. J. Lawin, P. E. Forssén, H. Ovrén. Efficient multi-frequency phase unwrapping using kernel density estimation. European Conference on Computer Vision(2016).
[24] F. Liu, J. Li, J. Lai, C. He. Full-frequency phase unwrapping algorithm based on multi-frequency heterodyne principle. Laser Optoelectron. Prog., 56, 011202(2019).
[25] E. H. Kim, J. Hahn, H. Kim, B. Lee. Profilometry without phase unwrapping using multi-frequency and four-step phase-shift sinusoidal fringe projection. Opt. Express, 17, 7818(2009).
[26] Y. Wang, L. Liu, J. Wu, X. Song, X. Chen, Y. Wang. Dynamic three-dimensional shape measurement with a complementary phase-coding method. Opt. Lasers Eng., 127, 105982(2020).
[27] S. Lv, Q. Sun, J. Yang, Y. Jiang, F. Qu, J. Wang. An improved phase-coding method for absolute phase retrieval based on the path-following algorithm. Opt. Lasers Eng., 122, 65(2019).
[28] Y. Wu, G. Wu, L. Li, Y. Zhang, H. Luo, S. Yang, J. Yan, F. Liu. Inner shifting-phase method for high-speed high-resolution 3-D measurement. IEEE Trans. Instrum. Meas., 69, 7233(2020).
[29] G. Wu, Y. Wu, L. Li, F. Liu. High-resolution few-pattern method for 3D optical measurement. Opt. Lett., 44, 3602(2019).
[30] S. Yang, G. Wu, Y. Wu, J. Yan, H. Luo, Y. Zhang, F. Liu. High-accuracy high-speed unconstrained fringe projection profilometry of 3D measurement. Opt. Laser Technol., 125, 106063(2020).
[31] L. Wang, Y. Chen, X. Han, Y. Fu, K. Zhong, G. Jiang. A 3D shape measurement method based on novel segmented quantization phase coding. Opt. Lasers Eng., 113, 62(2019).
[32] C. Zhou, T. Liu, S. Si, J. Xu, Y. Liu, Z. Lei. An improved stair phase encoding method for absolute phase retrieval. Opt. Lasers Eng., 66, 269(2015).
[33] M. Ma, P. Yao, J. Deng, H. Deng, J. Zhang, X. Zhong. A morphology phase unwrapping method with one code grating. Rev. Sci. Instrum., 89, 073110(2018).
[34] M. van de Giessen, J. P. Angelo, S. Gioux. Real-time, profile-corrected single snapshot imaging of optical properties. Biomed Opt. Express, 6, 4051(2015).
[35] H. H. Zou, X. Zhou, H. Zhao, T. Yang, H. B. Du, F. F. Gu, Z. X. Zhao. Color fringe-projected technique for measuring dynamic objects based on bidimensional empirical mode decomposition. Appl. Opt., 51, 3622(2012).
[36] J. Lai, J. Li, C. He, F. Liu. A robust and effective phase-shift fringe projection profilometry method for the extreme intensity. Optik, 179, 810(2019).
[37] Y. Yin, J. Mao, X. Meng, X. Yang, K. Wu, J. Xi, B. Sun. A two-step phase-shifting algorithm dedicated to fringe projection profilometry. Opt. Lasers Eng., 137, 106372(2021).
Get Citation
Copy Citation Text
Shichao Yang, Hanlin Huang, Gaoxu Wu, Yanxue Wu, Tian Yang, Fei Liu, "High-speed three-dimensional shape measurement with inner shifting-phase fringe projection profilometry," Chin. Opt. Lett. 20, 112601 (2022)
Category: Physical Optics
Received: Feb. 16, 2022
Accepted: Jun. 10, 2022
Posted: Jun. 13, 2022
Published Online: Jul. 14, 2022
The Author Email: Fei Liu (fei_liu@cqu.edu.cn)






