Laser propagating in under-dense plasma may trigger instabilities such as stimulated Raman scattering (SRS) and stimulated Brillouin scattering (SBS) where the laser decays into a scattered light and a plasma wave[1]. The laser–plasma instability (LPI) is one of the most troublesome obstacles to inertial confinement fusion (ICF). To achieve fusion, hundreds of laser beams are required to symmetrically irradiate the target, and these beams would inevitably overlap in plasma, forming a unique beam overlapping region different from the single-beam propagating region. The instability there is what we called the multibeam LPI[2].
High Power Laser Science and Engineering, Volume. 13, Issue 4, 04000e59(2025)
Spatial distributions of laser–plasma instability in the beam overlapping region
A reduced dispersion relation for multibeam laser–plasma instability is derived. The dispersion relation includes the combined effects of self-coupling and interaction with other beams by sharing a common scattered light (SL modes) and by sharing a common plasma wave (SP modes). The latter two have the most prominent collective effects of all. We have solved the dispersion relation numerically for stimulated Raman scattering, and set different beam configurations and polarizations to discuss the spatial distributions of the temporal growth rate. The instability in the beam overlapping region is complicated, but there are still a few simple rules that govern the system, such as the dominancy of SL modes and subdominancy of backscattering and SP modes. The maximum growth rate always occurs at these special modes, or a new mode formed by combining two or three of the special modes. The reduced model provides us with the ability to understand the underlying physics of multibeam instabilities under general laser and plasma conditions.
1 Introduction
Multibeam LPIs include many existing instabilities, such as cross-beam energy transfer (CBET)[3–5], which is two-beam SBS, and multibeam two-plasmon decay (TPD)[6–10], which is also based on two-beam interaction. More beams may introduce brand new features, such as unexpected scattering geometries[11–13], strengthened and collimating electron plasma waves[14–16]. There are two special modes associated with multibeam effects, one with a shared scattered light, which is called the SL mode, and the other with a shared plasma wave, which is called the SP mode[17]. The two modes constitute most of the dominant modes in the beam overlapping region. The multibeam instability strongly relies on the beam number, configurations and polarizations, so understanding the instability growth in the beam overlapping region with a general condition is of great importance, but it is still an open question. The dominant mode could be the SL mode, SP mode, backscattering, or another multibeam mode. A general method to determine the growth rates of all these modes is the key point to solve the problem.
Recently, we derived a general dispersion relation for multibeam SRS and SBS with an arbitrary beam number, configurations and polarizations, and obtained analytic growth rates for some special cases[18]. Although the general dispersion relation in the form of a determinant is largely simplified from the full dispersion relation of the
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
The 100 kJ laser facility in China[19] is used here, where four cones of
The paper is organized as follows. In Section 2, a reduced dispersion relation is derived. The key point of the polarization factor in the dispersion relation is established before we numerically solve the dispersion relation. In Section 3 we discuss the distribution of the SRS growth rate under various conditions, in order to understand the physics of multibeam instability step-by-step. Then we summarize and induce some simple rules valid for most common multibeam situations in Section 4. To verify the reduced model, 2D PIC simulations are also performed in Section 5. Finally, conclusions are given in Section 6.
2 Reduced dispersion relation for multibeam laser–plasma instability
The dispersion relation for SRS or SBS in multiple laser beams with arbitrary beam numbers, polarizations and configurations has been derived recently, in the form of a determinant[18], as follows:where the diagonal elements of the coefficient matrix are given by the following:
It is reduced from the full dispersion relation in a form of a determinant of the
In Ref. [18] we derived analytic results of the dispersion relation for two special cases, one with a shared scattered light, also called the SL mode, and the other with a shared plasma wave, called the SP mode. Other than these two special modes, the analytic growth rate of any scattering geometry is unavailable. Therefore, numerical calculations of Equation (1) are desperately needed to obtain the whole distribution of the growth rate in three dimensions. To make it feasible for numerical calculation, we further reduce the dispersion relation to a simpler form. Equation (1) can be transformed into the following:after some algebra, where
The double summation is now reduced to the single summation; however, one of the summations is still on the denominator. We could further turn this term into numerator by multiplying it on each side and noting that the terms in
The physics of the dispersion relation is clearly demonstrated: the first term on the right-hand side (RHS) is the self-matching or single-beam term of beam
One should also note that the reduced dispersion relation is for a particular beam
2.1 Some special solutions
The dispersion relation is analytic solvable under the following cases. Firstly, for single-beam interaction,
Let us assume
For
An analytic result emerges when
The wave number
On the other hand, when resonance occurs in the first and the third terms of Equation (5), the dispersion relation becomes the following:
Similarly, if
2.2 Roles of polarization
The multibeam dispersion relation relies heavily on the polarizations of incident beams, and the polarization of the scattered light is a degree of freedom, so we should deal with the polarization carefully. In the reduced dispersion relation, the polarization effect is imbedded in the factor
Here,
We consider both cases in our calculations. For the single-beam LPI,
Discussing how polarizations of multiple beams affect the distribution of temporal growth rate in three dimensions is one of our main goals of this paper. By numerically solving the reduced model with the above polarization determining schemes, we will see that in the next section.
3 Numerical results for multibeam growth rates
3.1 Numerical settings and benchmark via single-beam instability
In this section, distributions of the SRS temporal growth rates for one, two, four and eight beams under a variety of polarization combinations are numerically calculated and discussed. Our intention is to understand the underlying physics of the instability growth in the ambience of multiple overlapping laser beams, and obtain general laws characterizing the distributions and maximums of the growth rate under different polarizations.
Equation (5) is numerically solved for SRS in homogeneous plasmas. The spatial distribution is not sensitive to the plasma conditions and laser intensity, so we choose typical parameters in ICF,
The 100 kJ laser facility[19] is used here for discussion. The laser configuration is shown in Figure 1. There are 48 beams in total delivering a maximum 180 kJ energy. The beams are incident on four cones of different angles relative to the hohlraum axis:
![]()
Figure 1.Spatial distributions of the single-beam SRS growth rate: (a) s-polarized beam denoted by the green rectangle and (b) p-polarized beam denoted by the blue rectangle. The unit of the growth rate is 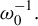
The growth rate of multibeam instability is the imaginary part of the solution (frequency) of Equation (5) as a function of the wave vector,
Figure 1 shows the distribution of the single-beam growth rate. The green rectangle denotes the s-polarized incident beam and the blue rectangle denotes the p-polarized incident beam. The theoretical single-beam growth rate predicts that the maximum growth mode is backscattering with
3.2 Two-beam interactions
In a single-beam instability, backscattering is always the most unstable mode in homogeneous plasmas due to its largest wave number being that of the plasma wave; however, it is not always true for multibeam instabilities. Here we will show several distributions of growth rates under two, four and eight beams, and try to find the rules that govern the multibeam physics. Most of the time the maximum growth rate is that of some special modes, such as the SL mode, SP mode or (near) backward mode; these modes have received the most attention in our discussions.

Table 1. Average polarization factor
 of the SL mode and SP mode under different polarization configurations. The black, red and green arrows in the insets represent the wave vectors of incident lights, scattered lights and plasma waves, respectively.
of the SL mode and SP mode under different polarization configurations. The black, red and green arrows in the insets represent the wave vectors of incident lights, scattered lights and plasma waves, respectively.Table 1. Average polarization factor
 of the SL mode and SP mode under different polarization configurations. The black, red and green arrows in the insets represent the wave vectors of incident lights, scattered lights and plasma waves, respectively.
of the SL mode and SP mode under different polarization configurations. The black, red and green arrows in the insets represent the wave vectors of incident lights, scattered lights and plasma waves, respectively.SL mode SP mode Configuration S 1 1 P ${\cos}^2\theta$ ${\cos}^2\alpha$ S-P 1/2 $(1+{\cos}^2\alpha )/2$ S/8S 1/2 1 P/8P ${\cos}^2\theta /2$ ${\cos}^2\alpha$ S-P-S-P $(1+{\cos}^2\theta )/2$ $(1+{\cos}^2\alpha )/2$ S–2P/4S–4P $(1+{\cos}^2\theta )/4$ $(1+{\cos}^2\alpha )/2$
Since the plasma wave number of the SL mode is larger than that of the SP mode (shown in green arrows in the insets of Table 1), we have
Figure 2 shows growth rate distributions of two s-polarized beams for four different incidence angles. The green rectangles denote the s-polarized beams, while the bold one is the specific
![]()
Figure 2.Distributions of growth rates of two s-polarized beams (green rectangles) under four incidence angles: (a) 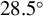 , (b)
, (b) 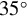 , (c)
, (c) 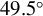 and (d)
and (d) 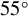 . The resonant beam is shown with a bold rectangle. The modes with the maximum growth rate are marked by a white ‘X’.
. The resonant beam is shown with a bold rectangle. The modes with the maximum growth rate are marked by a white ‘X’.

Table 2. A summary of the maximum growth rates under different polarization configurations when
 (denoted by ‘Maximum’). The growth rate of a backward scattered seed whose polarization is aligned with the resonant beam is also evaluated under the same conditions (denoted by ‘Backward’).
(denoted by ‘Maximum’). The growth rate of a backward scattered seed whose polarization is aligned with the resonant beam is also evaluated under the same conditions (denoted by ‘Backward’).Table 2. A summary of the maximum growth rates under different polarization configurations when
 (denoted by ‘Maximum’). The growth rate of a backward scattered seed whose polarization is aligned with the resonant beam is also evaluated under the same conditions (denoted by ‘Backward’).
(denoted by ‘Maximum’). The growth rate of a backward scattered seed whose polarization is aligned with the resonant beam is also evaluated under the same conditions (denoted by ‘Backward’).Configuration 2S 2P S-P P-S 4S 4P S-P-S-P S-S-P-P 8S 8P 4S-4P Maximum $(\times {10}^{-4}{\omega}_0^{-1})$ 11.0 8.3 8.4 9.6 11.0 10.4 12.4 10.3 14.7 11.8 12.4 Backward $(\times {10}^{-4}{\omega}_0^{-1})$ 9.7 8.3 8.3 9.6 9.2 9.3 9.8 8.9 9.4 9.9 9.4
Figure 3 shows the growth rates under two p-polarized beams (blue rectangles). The average polarization factor is
![]()
Figure 3.Distributions of growth rates of two p-polarized beams (blue rectangles) under four incidence angles: (a) 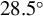 , (b)
, (b) 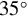 , (c)
, (c) 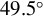 and (d)
and (d) 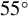 .
.
Figure 3 represents such interactions. When
The last two cases are the combination of an s-polarized beam and a p-polarized beam. The polarization directions of these two beams are perpendicular to each other, so one would expect an inefficient coupling of two beams. The average polarization factors are
Figure 4 shows typical cases of
![]()
Figure 4.Distributions of growth rates of an s-polarized beam (green rectangle) and a p-polarized beam (blue rectangle): (a) the resonant beam is s-polarized (S-P interactions), while (b) the resonant beam is p-polarized (P-S interactions).
3.3 Four-beam interactions
Complexity grows exponentially as the number of incident beams increases. The results obtained from few beams are usually not appropriate for situations with more beams; however, we could still look for some general rules for multibeam interactions. For the four-beam interactions discussed in this section, we concentrate on four polarization combinations: four s-polarized beams (4S), four p-polarized beams (4P), the maximum coupling case (S-P-S-P) and half-s-half-p (S-S-P-P or 2S-2P). The four beams are symmetrically distributed.
Four s-polarized beams are perhaps the simplest case of all. We still first discuss the theoretical growth rates of some special modes to estimate a general view of this multibeam system. The average polarization factors for the SL mode and SP mode are
Since the SP mode shares a common plasma wave, each scattered light could couple with its incident light individually, and the coupling factor is always maximized. From then on the SP mode could become enhanced, or even dominant under specific conditions. Owing to the increasing beam number, the multiplier increases as
Distributions of four s-polarized beams are shown in Figures 5(a) and 5(c). For
![]()
Figure 5.Distributions of growth rates of four incident beams: (a)–(f) are varied in polarization configurations and incident angles as depicted in each plot.
Four p-polarized beams are the least coupling combination of all. The average polarization factors are
Obviously
Figures 5(b) and 5(d) show the distribution of 4P cases when
For a more complex polarization configuration, the distribution of the growth rate could be intricate. Here we discuss the cases of S-P-S-P and S-S-P-P and plot their distributions when
3.4 Eight-beam interactions
Finally, let us take a look at the eight-beam interaction, which is usually the maximum beam/quad number of a cone in many laser facilities, such as the NIF and the 100 kJ laser facility discussed here. We choose three polarization combinations: all s-polarized beams, all p-polarized beams and half-s-half-p beams. As shown in Table 1, the average polarization factors are the same as the corresponding four beam cases; therefore, we expect that the physics will remain the same.
Figure 6 shows the distributions of eight-beam interactions under various conditions. First of all, the backward scattering is further out of dominance. The discrepancy between the backward scattering and the true multibeam mode with the maximum growth rate is becoming larger, as shown in Table 2.
![]()
Figure 6.Distributions of growth rates of eight incident beams: (a)–(i) are varied in polarization configurations and incidence angles as described in the top and left.
Specifically, let us discuss the case of 8S first. Figure 6(a) uses two inner cones as incident beams. The SL mode in the center is the dominant mode. We find that the distributions are more localized, especially along the two bisectors between the resonant beam and its nearest beams. The SP mode is weak here, owing to fewer interactions with other special modes. We find that when the incidence angle is very small, such as a few degrees, the SP mode would be dominant in the multibeam system. As for the 8P cases shown in the second row, the physics is very similar to that in the 4P cases. The two symmetric growth rates along the nearest bisectors dominate those cases. Many spoke-shape distributions along the bisectors and incident beams are a characteristic of p-polarized beams. In the case of half-s-half-p, the asymmetric mode dominates the distribution; however, since it includes a large number of s-polarized beams, the exact backward SL mode dominates the system.
4 An inference of general rules that govern the growth of multibeam systems
SRS and SBS are similar LPIs in that an incident electromagnetic wave decays into a scattered electromagnetic wave and an electrostatic plasma wave. The physics of instability growth in the multiple beam overlapping region shares similar features. We have also calculated distributions of SBS growth rates under various conditions and found that the behaviors of the maximum growth rate, SL mode, SP mode and backward scattering look the same with SRS. The differences are only in the magnitude of the growth rate and the spread width of those modes. However, if the frequencies of incident beams change a little, the multibeam mode of SBS changes dramatically due to the tinny frequency of the ion acoustic wave. This could give rise to CBET. For SRS, a slight frequency change will barely affect the distribution. This effect is not the purpose of this paper.
From the above analyses of the effect of a few beam and polarization configurations on the growth rate distribution, we can infer some general rules that govern the growth of multibeam systems.
5 Spatial distributions obtained from particle-in-cell simulations
To verify the reduced model, we have performed 2D PIC simulations of SRS with two crossing laser beams using EPOCH code. A three-dimensional PIC simulation of more beams is time-consuming, so it is not presented in this paper. The spatial distributions of scattered light characterized by angular distribution in the plane of incidence are plotted in Figure 7.
![]()
Figure 7.Particle-in-cell simulations of two-beam SRS in two-dimensions. The left-hand and middle columns show the time-averaged longitudinal and transverse field spectra, respectively: two s-polarized beams incident with (a) 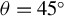 , (d)
, (d) 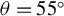 , and a p-polarized beam (upper) and an s-polarized beam (lower) incident with (g)
, and a p-polarized beam (upper) and an s-polarized beam (lower) incident with (g) 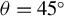 . The figures in the right-hand column are the corresponding spatial distributions of scattered light, which are interpolated along circles in the left-hand figures. The center (
. The figures in the right-hand column are the corresponding spatial distributions of scattered light, which are interpolated along circles in the left-hand figures. The center (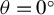 ) indicates scattered light along the
) indicates scattered light along the 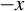 direction.
direction.
The simulation setup is similar to our previous paper[12]. Two laser beams with the same intensity
The time-averaged field spectra in the overlapping region are shown in Figure 7. The left-hand column shows the longitudinal field spectra, the middle column shows the transverse field spectra and the right-hand column shows the corresponding spatial distributions of scattered light. Two types of spatial distributions are shown here: the red and green curves are interpolated from the dispersion relation on the longitudinal field spectra (left), and blue or magenta dotted curves are interpolated from the dispersion relation on the transverse field spectra (middle or left). As we can see, the two metrics of scattered light spectra seem to have little difference in shape. For the metric of longitudinal spectra (solid curves), the two spatial distributions are nearly the same for the two s-polarized beams in the first two rows. For the s-p combination shown in the third row where the upper beam is p-polarized and lower beam is s-polarized, the spectra differ both in shape and amplitude. The scattered amplitude of the p-polarized beam (polarized in the
The collective mode excited by the two overlapping beams is also apparent. For two s-polarized beams, the dominant mode is the SL mode propagating along the symmetry axis where the polar angle is 0. This mode is away from the backscattering indicated by black-dashed lines in Figures 7(c) and 7(f). As we change the upper beam from s-polarization to p-polarization, the dominant mode changes to near backscattering, as shown in Figure 7(i). These results are qualitatively consistent with Figures 2 and 4, showing good agreement between the reduced model and PIC simulations.
The reduced model is based on the assumption that the laser beam is monochromatic and the plane wave and plasma are homogeneous. It is also a linear analysis of the wave coupling equations. In the PIC simulations, we find that although nonlinear phenomenon (here the nonlinear frequency shift[12]) occurs, the main physics that the SL mode is dominant still remains. For more realistic conditions, new modes such as side scatterings in inhomogeneous plasma would compete with the multibeam modes, and laser speckles, which introduce a spread on the incidence angles, also affect the spectrum of the multibeam mode. The reduced model could be easily extended to include multicolor incident beams, allowing the description of the effect of CBET, but the broadband laser is beyond this simple model. Nonlinear phenomena, such as laser filamentation and the kinetic effect, are not included here, and need more detailed kinetic simulations. Therefore, the reduced model could be a quick approach to obtain the linear physics of multibeam instabilities; however, it is also limited in more complex situations. The model verified by PIC simulations could be added into more sophisticated models, such as the ray-tracing model, to extend its application.
6 Conclusions
In this paper, we have obtained a reduced dispersion relation for multibeam LPIs, which is easily turned into numerical calculations. The dispersion relation consists of three main effects: self-coupling, SL modes and SP modes. Then we solve the dispersion relation numerically under various beam numbers, configurations and polarizations in order to understand the physics of multibeam instability with general conditions. The growth of instability in the beam overlapping region is complicated; however, a few general results could be deduced, such as the dominancy of the SL mode and the subdominancy of backscattering and the SP mode. The 2D PIC simulation results also show good agreement with the reduced model. The dispersion relation provides us with a strong tool to deeply excavate the instability in the overlapping region, which has not been done before.
Appendix. Dispersion relation with respect to scattered light
All the dispersion relations discussed above, from
Therefore, the coupling equation can be rewritten to a simplified form:
[1] P. Michel. Introduction to Laser-Plasma Interactions(2023).
[2] J. F. Myatt, J. Zhang, R. W. Short, A. V. Maximov, W. Seka, D. H. Froula, D. H. Edgell, D. T. Michel, I. V. Igumenshchev, D. E. Hinkel, P. Michel, J. D. Moody. Phys. Plasmas, 055501(2014).
[3] W. L. Kruer, S. C. Wilks, B. B. Afeyan, R. K. Kirkwood. Phys. Plasmas, 3, 382(1996).
[4] P. Michel, L. Divol, E. A. Williams, S. Weber, C. A. Thomas, D. A. Callahan, S. W. Haan, J. D. Salmonson, S. Dixit, D. E. Hinkel, M. J. Edwards, B. J. MacGowan, J. D. Lindl, S. H. Glenzer, L. J. Suter. Phys. Rev. Lett., 102, 025004(2009).
[5] I. V. Igumenshchev, D. H. Edgell, V. N. Goncharov, J. A. Delettrez, A. V. Maximov, J. F. Myatt, W. Seka, A. Shvydky, S. Skupsky, C. Stoeckl. Phys. Plasmas, 17, 122708(2010).
[6] D. T. Michel, A. V. Maximov, R. W. Short, S. X. Hu, J. F. Myatt, W. Seka, A. A. Solodov, B. Yaakobi, D. H. Froula. Phys. Rev. Lett., 109, 155007(2012).
[7] H. X. Vu, D. F. DuBois, D. A. Russell, J. F. Myatt. Phys. Plasmas, 17, 072701(2010).
[8] J. Zhang, J. F. Myatt, R. W. Short, A. V. Maximov, H. X. Vu, D. F. DuBois, D. A. Russell. Phys. Rev. Lett., 113, 105001(2014).
[9] R. K. Follett, J. G. Shaw, J. F. Myatt, D. H. Froula, J. P. Palastro. Phys. Rev. E, 043214(2020).
[10] G. Cristoforetti, P. Koester, S. Atzeni, D. Batani, S. Fujioka, Y. Hironaka, S. Hüller, T. Idesaka, K. Katagiri, K. Kawasaki, R. Kodama, D. Mancelli, P. Nicolai, N. Ozaki, A. Schiavi, K. Shigemori, R. Takizawa, T. Tamagawa, D. Tanaka, A. Tentori, Y. Umeda, A. Yogo, L. A. Gizzi. High Power Laser Sci. Eng., 11, e24(2023).
[11] S. Depierreux, C. Neuville, C. Baccou, V. Tassin, M. Casanova, P.-E. Masson-Laborde, N. Borisenko, A. Orekhov, A. Colaitis, A. Debayle, G. Duchateau, A. Heron, S. Huller, P. Loiseau, P. Nicolaï, D. Pesme, C. Riconda, G. Tran, R. Bahr, J. Katz, C. Stoeckl, W. Seka, V. Tikhonchuk, C. Labaune. Phys. Rev. Lett., 117, 235002(2016).
[12] S. J. Yang, H. B. Zhuo, Y. Yin, Z. J. Liu, C. Y. Zheng, X. T. He, C. Z. Xiao. Phys. Rev. E, 102, 013205(2020).
[13] J. Qiu, L. Hao, L. Cao, S. Zou. Matter Radiat. Extremes, 6, 065903(2021).
[14] P. Michel, L. Divol, E. L. Dewald, J. L. Milovich, M. Hohenberger, O. S. Jones, L. Berzak Hopkins, R. L. Berger, W. L. Kruer, J. D. Moody. Phys. Rev. Lett., 115, 055003(2015).
[15] C. Neuville, V. Tassin, D. Pesme, M.-C. Monteil, P.-E. Masson-Laborde, C. Baccou, P. Fremerye, F. Philippe, P. Seytor, D. Teychenné, W. Seka, J. Katz, R. Bahr, S. Depierreux. Phys. Rev. Lett., 116, 235002(2016).
[16] Q. Wang, Z. Li, Z. Liu, T. Gong, W. Zhang, T. Xu, B. Li, P. Li, X. Li, C. Zheng, L. Cao, X. Liu, K. Pan, H. Zhao, Y. Liu, B. Deng, L. Hou, Y. Li, X. Liu, Y. Li, X. Peng, Z. Guan, Q. Wang, X. Che, S. Li, Q. Yin, W. Zhang, L. Xia, P. Wang, X. Jiang, L. Guo, Q. Li, M. He, L. Hao, H. Cai, W. Zheng, S. Zou, D. Yang, F. Wang, J. Yang, B. Zhang, Y. Ding, X. He. Matter Radiat. Extremes, 8, 055602(2023).
[17] D. F. DuBois, B. Bezzerides, H. A. Rose. Phys. Fluids B, 4, 241(1992).
[18] C. Z. Xiao, H. B. Zhuo, Y. Yin, Z. J. Liu, C. Y. Zheng, X. T. He. Phys. Plasmas, 26, 062109(2019).
[19] F. Wang, S. Jiang, Y. Ding, S. Liu, J. Yang, S. Li, T. Huang, Z. Cao, Z. Yang, X. Hu, W. Miao, J. Zhang, Z. Wang, G. Yang, R. Yi, Q. Tang, L. Kuang, Z. Li, D. Yang, Y. Li, X. Peng, K. Ren, B. Zhang. Matter Radiat. Extremes, 5, 035201(2020).
[20] C. Chen, T. Gong, Z. Li, L. Hao, Y. Liu, X. Liu, H. Zhao, Y. Liu, K. Pan, Q. Li, S. Li, Z. Li, S. Jin, F. Wang, D. Yang. Matter Radiat. Extremes, 9, 027601(2024).
[21] J. D. Moody, P. Michel, L. Divol, R. L. Berger, E. Bond, D. K. Bradley, D. A. Callahan, E. L. Dewald, S. Dixit, M. J. Edwards, S. Glenn, A. Hamza, C. Haynam, D. E. Hinkel, N. Izumi, O. Jones, J. D. Kilkenny, R. K. Kirkwood, J. L. Kline, W. L. Kruer, G. A. Kyrala, O. L. Landen, S. LePape, J. D. Lindl, B. J. MacGowan, N. B. Meezan, A. Nikroo, M. D. Rosen, M. B. Schneider, D. J. Strozzi, L. J. Suter, C. A. Thomas, R. P. J. Town, K. Widmann, E. A. Williams, L. J. Atherton, S. H. Glenzer, E. I. Moses. Nat. Phys., 8, 344(2012).
Get Citation
Copy Citation Text
Chengzhuo Xiao, Kaiqiang Pan, Han Wen, Tao Gong, Zhichao Li, Ji Yan, Jinqing Yu, Dong Yang. Spatial distributions of laser–plasma instability in the beam overlapping region[J]. High Power Laser Science and Engineering, 2025, 13(4): 04000e59
Category: Research Articles
Received: Nov. 25, 2024
Accepted: May. 15, 2025
Published Online: Sep. 15, 2025
The Author Email: Chengzhuo Xiao (xiaocz@hnu.edu.cn), Tao Gong (gongtaolfrc@163.com)







 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence

