Beams of MeV-energy fast electrons can be created via irradiation of high-intensity
High Power Laser Science and Engineering, Volume. 13, Issue 2, 02000e14(2025)
An investigation of the emittance of escaping fast electron beams from planar and nanowire targets
Fast electron generation and transport in high-intensity laser–solid interactions induces X-ray emission and drives ion acceleration. Effective production of these sources hinges on an efficient laser absorption into the fast electron population and control of divergence as the beam propagates through the target. Nanowire targets can be employed to increase the laser absorption, but it is not yet clear how the fast electron beam properties are modified. Here we present novel measurements of the emittance of the exiting fast electron beam from irradiated solid planar and nanowire targets via a pepper-pot diagnostic. The measurements indicate a greater fast electron emittance is obtained from nanowire targets. Two-dimensional particle-in-cell simulations support this conclusion, revealing beam defocusing at the wire–substrate boundary, a higher fast electron temperature and transverse oscillatory motion around the wires.
1 Introduction
Characterization of the fast electrons is crucial to determine suitable applications of these sources. The energies of the escaping fast electron beam can be measured to recover the energy spectra of the fast electron population[11]. In a study by Honrubia and Meyer-ter-Vehn[12], the energy fraction deposited into FI-relevant dense targets was found to be sensitive to the average kinetic energy of the beam, demonstrating that the efficiency of the interaction has a dependence on the electron energy spectra. It is well-established that the fast electron beam possesses an intrinsic divergence[13,14]; in the context of FI this could result in energy deposition occurring over a larger volume than the hotspot volume[15]. The divergence of the beam can also influence the properties of bremsstrahlung X-ray emission, as highlighted by Armstrong et al.[16], where it was found that a reduction of the divergence yielded a preferential source for imaging. In addition, the divergence of the beam results in a reduced current density
In general, an electron beam is characterized by the emittance, a measure of the area of position-momentum space occupied by the electron population[19–21]. The total root mean square (rms) emittance of a population of particles along the transversal x-axis can be given as follows:
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
Many fast electron transport studies have employed planar foil targets. More recently, the use of nanowire (NW) targets has attracted growing interest on account of an observed increase in laser absorption[22–26]. Due to the relative novelty of these targets open questions remain on the influence of the wires on the absorption, fast electron generation and transport and the beam properties. An increased temperature of the fast electron population has been frequently reported from these NW targets[27–30], which could correlate with an increase in the phase space and thus the emittance of the electrons. Jiang et al.[31] proposed a target design with ‘tower’ structures on the front surface that facilitated the generation of higher energy electrons concurrent with a narrower angular cone of emission when compared to planar targets. The simulations used a large wire spacing with respect to the laser spot size (2 μm vacuum gap size and 2.9 μm full width at half maximum (FWHM) spot size), which facilitated the direct laser acceleration (DLA) mechanism, and only considered the highest energy electrons that were considered to be optimally positioned to undergo DLA. Imaging of X-ray emission at the front and rear surfaces of nanobrush targets by Zhao et al.[32] suggested collimation of the electron beam by the wire-like front structures. However, there is little other recorded experimental evidence of this guiding effect. Furthermore, it is not clear how, or indeed if, this guiding translates into an effect on the emittance of the exiting fast electron beam.
In this paper we present the first experimental measurements of the emittance of the exiting fast electron beam generated from intense laser interactions with solid targets. A pepper-pot diagnostic was employed to obtain transverse emittance estimates in a novel measurement for fast electrons generated from laser–solid interactions. The results indicate an increased emittance of the electron beam generated from the NW target compared to the planar target. Simulations using the two-dimensional (2D) particle-in-cell (PIC) code EPOCH are used to elucidate the fast electron transport along the wires. We show that electrons with energies close to the ponderomotive energy are confined to the wires by the electromagnetic (EM) fields established around the structures. In addition, the simulations reveal the growth of a defocusing magnetic field at the wire–substrate boundary that can strongly influence the fast electron transport and the overall beam emittance.
2 Pepper-pot diagnostic
A pepper-pot diagnostic can be used to obtain an estimate of the electron beam emittance[19,33]. The setup of a pepper-pot diagnostic is depicted in Figure 1. The approach involves passing the beam of particles through a mask with an array of holes of known diameter and spacing. This divides the larger beam into several smaller beamlets. These beamlets propagate a distance,
The mean divergence can be retrieved from the hole and beamlet positions as
![]()
Figure 1.Illustration of the pepper-pot setup. In this configuration the fast electrons propagate from left to right. The image on the far-right shows a sample of the raw data obtained from the experimental work in this paper.
3 Experimental results
The experimental work was conducted at the ILIL facility at INO-CNR, Pisa[35]. The ILIL-PW Ti:sapphire laser line was used to irradiate both planar and NW-coated targets. The NWs were produced via chemical bath deposition[36] onto a
An acknowledged concern with the use of nanostructured targets in intense laser interactions is the disruption of the structures by the laser pedestal or pre-pulses prior to the arrival of the main pulse[37]. The use of a high-contrast laser profile can improve the prospects of retaining the structures until the main pulse interaction. One approach is to frequency double the laser pulse with an appropriate non-linear crystal. In the experiment, second harmonic generation of the 800 nm laser pulse was achieved using a potassium dihydrogen phosphate (KDP) crystal placed immediately after the compressor, creating pulses with a wavelength
![]()
Figure 2.(a) Layout of the experimental setup in the vacuum chamber. A pepper-pot diagnostic is placed behind the irradiated target; (b) shows the setup of the pepper-pot. (c) The orientation of the laser fields with respect to the target.
As anticipated, the emittance of the exiting fast electron beam is estimated using a pepper-pot diagnostic setup. Figure 2(a) shows the positioning of the pepper-pot in the target chamber. The pepper-pot mask has a
The emittance formula in Equation (2) is used to calculate a transverse fast electron emittance in x (perpendicular to the laser
![]()
Figure 3.Experimental estimate of the transverse emittance in (a)
4 Particle-in-cell simulations
Simulations using the PIC code EPOCH[38] are carried out to explore the laser interaction with the NW and planar targets. A domain is established of size
![]()
Figure 4.Initial ion density of the (a) planar and (b) nanowire targets modelled in the PIC simulations. The arrow indicates the direction of the incoming laser, irradiating the targets at an angle of 15°. The dashed line indicates the position of the probe plane. The energy spectra of the fast electrons are shown in (c) for the planar and nanowire targets. Plots (d)–(f) show the angular emittance of the fast electrons recorded at the probe plane for the different cases. In (d) the transverse emittance from the s-polarized planar case is shown, which corresponds to the emittance perpendicular to the laser
The
In the PIC simulations the laser propagates in the z-direction and the transverse properties of the fast electrons are taken in the x-direction (in two dimensions we cannot explore the y-direction). Therefore, in order to explore both
4.1 Fast electron properties
A probe plane is placed at
An estimate of the emittance of the injected fast electron beams in the planar and NW targets can also be obtained from the diagnostic probe. The crossing position x and angle
A similar emittance plot is constructed for the fast electrons from the NW target. Figure 4(f) shows a highly structured profile with a fraction of the electrons remaining close to the central positions of the wires with a low angular divergence, supporting the argument that the wires can sustain some guiding up to the substrate. The electrons possess a large angular spread from each wire up to
4.2 Electron trajectories
The trajectories of a random subset of individual particles can be extracted from the PIC simulations in order to delve into the influence of the wires on the electron transport. Figure 5(a) shows the trajectories of the highest energy electrons from the p-polarized interaction with the planar target. The electrons are injected at an angle along the laser
![]()
Figure 5.Electron trajectories from a random subset of hot electrons from the p-polarized laser interactions. The electron path is plotted across 120 fs, and is labelled according to the maximum energy reached during the simulation. Figures (a) and (b) show example trajectories of the highest energy electrons for the planar and nanowires respectively, and (c) shows example trajectories of lower energy electrons with 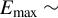 400 keV from the nanowire interaction.
400 keV from the nanowire interaction.
The emittance plot in Figure 4(f) indicates the wires are influencing the transport of the fast electrons. Figure 5(b) shows the paths travelled by electrons heated to a maximum energy
4.3 EM field growth
The EM fields around the wires are inspected to explain the trajectories of the fast electrons revealed in the simulations. Figures 6(a) and 6(b) show the evolution of the
![]()
Figure 6.(a) 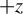 -direction.
-direction.
In addition to the ‘local’ fields around a single wire, it can be instructive to also look at the ‘global’ fields across the larger simulation domain. Figure 6(c) shows the
5 Discussion
PIC simulations have revealed the evolution of strong electric and magnetic fields around the wires that affect the fast electron transport. At early times the fields inside the NW channels due to laser propagation and SPP excitation can extract and accelerate electrons from the wires[45]. At later times a prominent quasistatic field structure is instead evident. As the electrons are extracted from the wires, a charge separation will be established between the wire and vacuum regions. This will result in the generation of an electrostatic Ex field between the wires.
Figure 7(a) shows the averaged current densities along the wires at a time
![]()
Figure 7.(a) Current density 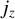 averaged in the range
averaged in the range 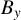 fields (orthogonal to the simulation plane) within the same region.
fields (orthogonal to the simulation plane) within the same region.
For an electron propagating along a wire in z, the
![]()
Figure 8.The transverse momenta of two example fast electrons as they traverse the wire region. The blue trajectory is for an electron with a final energy close to the ponderomotive temperature, and the red trajectory is for one of the highest energy MeV electrons.
Whilst evidence has been presented here demonstrating the ability of the NWs to guide the electrons under particular conditions, the geometry is clearly not optimized to reduce the final emittance. Many electrons undergo an oscillatory motion around the wires and their transverse momenta are hardly reduced by the NW structures, and are even enhanced compared to planar targets, as shown in Figures 4(e) and 4(f). Since the fields responsible for inducing the oscillatory nature of the fast electron transport are a consequence of extracting and accelerating the electrons from the wires, it may be difficult to avoid this entirely.
The larger azimuthal magnetic field at the wire–substrate boundary has been explored and identified elsewhere in intense laser interactions with planar targets[50–53], primarily on the effect on sheath-accelerated protons at the rear surface. These self-generated magnetic fields at the front surface of the target can be attributed to the ‘fountain effect’[54–56] arising from the interplay between the counter-propagating injected fast electron and return currents. Fast electrons propagating through the +
A consideration of these generated fields is vital for full exploitation of the wires as fast electron guiding elements. A mitigation of the defocusing magnetic field growth at the wire–substrate interface could be realized through proper choice of laser-target parameters. For example, since the strength of the magnetic field generated scales with the injected fast electron current density[57], a larger focal spot could be implemented to reduce the deflection experienced by the fast electrons accelerated in the wires. In addition, lower energy electrons appear to be more readily guided along the wires and suffer less deflection due to the
Finally, we note that the 2D simulations of NW targets are inherently inaccurate to reproduce the target geometry since they model infinite ‘slabs’ in the y-direction. Simulation studies by Fedeli et al.[48] and Jiang et al.[31] compared the effectiveness of 2D simulations as a means of reproducing three-dimensional (3D) simulations. Whilst the qualitative results could be reproduced, there were differences observed in the final laser absorption and electron temperatures. However, the EM fields between the wire gaps should be reliably reproduced in two dimensions for this wire diameter and spacing, as should the transverse guiding of the electrons. In addition, the generation of the azimuthal
6 Conclusion
NW targets are frequently endorsed as a means to attain higher laser absorption into fast electrons. Enhanced coupling into fast electrons, resulting in an increased electron flux or temperature, is well-recognized, as is the potential for the wires to guide the electrons. Less attention has been paid to the transport of the electrons as they exit the influence of the wires and the effect of the wires on the overall electron beam properties. The experimental measurements reported here suggest an increased emittance of the escaping fast electron beam from the NW targets. PIC simulations explain this increase in emittance not only by an increased hot electron temperature, but also through the discovery of a self-generated magnetic field growing at the wire–substrate boundary that serves to defocus the electron beam. Further work on the use of NW targets as an efficient fast electron beam source should consider this field generation carefully. The detrimental effects on the beam emittance could be reduced by employing appropriate wire geometries and laser parameters.
[1] C. M. Brenner, S. R. Mirfayzi, D. R. Rusby, C. Armstrong, A. Alejo, L. A. Wilson, R. Clarke, H. Ahmed, N. M. H. Butler, D. Haddock, A. Higginson, A. McClymont, C. Murphy, M. Notley, P. Oliver, R. Allott, C. Hernandez-Gomez, S. Kar, P. McKenna, D. Neely. Plasma Phys. Control. Fusion, 58, 014039(2016).
[2] L. A. Gizzi, A. Giulietti, D. Giulietti, P. Köster, L. Labate, T. Levato, F. Zamponi, A. Lübcke, T. Kämpfer, I. Uschmann, E. Förster, A. Antonicci, D. Batani. Plasma Phys. Control. Fusion, 49, B211(2007).
[3] P. Köster, K. Akli, D. Batani, S. Baton, R. G. Evans, A. Giulietti, D. Giulietti, L. A. Gizzi, J. S. Green, M. Koenig, L. Labate, A. Morace, P. Norreys, F. Perez, J. Waugh, N. Woolsey, K. L. Lancaster. Plasma Phys. Control. Fusion, 014007(2009).
[4] D. R. Rusby, C. D. Armstrong, G. G. Scott, M. King, P. McKenna, D. Neely. High Power Laser Sci. Eng., 7, e45(2019).
[5] R. A. Snavely, M. H. Key, S. P. Hatchett, T. E. Cowan, M. Roth, T. W. Phillips, M. A. Stoyer, E. A. Henry, T. C. Sangster, M. S. Singh, S. C. Wilks, A. Mackinnon, A. Offenberger, D. M. Pennington, K. Yasuike, A. B. Langdon, B. F. Lasinski, J. Johnson, M. D. Perry, E. M. Campbell. Phys. Rev. Lett., 85, 2945(2000).
[6] S. C. Wilks, A. B. Langdon, T. E. Cowan, M. Roth, M. Singh, S. Hatchett, M. H. Key, D. Pennington, A. MacKinnon, R. A. Snavely. Phys. Plasmas, 8, 542(2001).
[7] Y. Sentoku, T. E. Cowan, A. Kemp, H. Ruhl. Phys. Plasmas, 10, 2009(2003).
[8] V. Malka, S. Fritzler, E. Lefebvre, E. d’Humières, R. Ferrand, G. Grillon, C. Albaret, S. Meyroneinc, J.-P. Chambaret, A. Antonetti, D. Hulin. Med. Phys., 31, 1587(2004).
[9] S. Malko, W. Cayzac, V. Ospina-Bohórquez, K. Bhutwala, M. Bailly-Grandvaux, C. McGuffey, R. Fedosejevs, X. Vaisseau, A. Tauschwitz, J. I. Apiñaniz, D. De Luis Blanco, G. Gatti, M. Huault, J. A. Perez Hernandez, S. X. Hu, A. J. White, L. A. Collins, K. Nichols, P. Neumayer, G. Faussurier, J. Vorberger, G. Prestopino, C. Verona, J. J. Santos, D. Batani, F. N. Beg, L. Roso, L. Volpe. Nat. Commun., 13, 2893(2022).
[10] M. Tabak, J. Hammer, M. E. Glinsky, W. L. Kruer, S. C. Wilks, J. Woodworth, E. M. Campbell, M. D. Perry, R. J. Mason. Phys. Plasmas, 1, 1626(1994).
[11] O. Culfa, G. J. Tallents, A. K. Rossall, E. Wagenaars, C. P. Ridgers, C. D. Murphy, R. J. Dance, R. J. Gray, P. McKenna, C. D. R. Brown, S. F. James, D. J. Hoarty, N. Booth, A. P. L. Robinson, K. L. Lancaster, S. A. Pikuz, A. Y. Faenov, T. Kampfer, K. S. Schulze, I. Uschmann, N. C. Woolsey. Phys. Rev. E, 93, 043201(2016).
[12] J. J. Honrubia, J. Meyer-ter-Vehn. Nucl. Fusion, 46, L25(2006).
[13] J. S. Green, V. M. Ovchinnikov, R. G. Evans, K. U. Akli, H. Azechi, F. N. Beg, C. Bellei, R. R. Freeman, H. Habara, R. Heathcote, M. H. Key, J. A. King, K. L. Lancaster, N. C. Lopes, T. Ma, A. J. MacKinnon, K. Markey, A. McPhee, Z. Najmudin, P. Nilson, R. Onofrei, R. Stephens, K. Takeda, K. A. Tanaka, W. Theobald, T. Tanimoto, J. Waugh, L. Van Woerkom, N. C. Woolsey, M. Zepf, J. R. Davies, P. A. Norreys. Phys. Rev. Lett., 100, 015003(2008).
[14] A. Debayle, J. J. Honrubia, E. d’Humières, V. T. Tikhonchuk. Phys. Rev. E, 82, 036405(2010).
[15] C. Bellei, L. Divol, A. J. Kemp, M. H. Key, D. J. Larson, D. J. Strozzi, M. M. Marinak, M. Tabak, P. K. Patel. Phys. Plasmas, 20, 052704(2013).
[16] C. D. Armstrong, G. Liao, H. Liu, Y. Li, Z. Zhang, Y. Zhang, B. Zhu, P. Bradford, N. C. Woolsey, P. Oliveira, C. Spindloe, W. Wang, P. McKenna, D. Neely. Plasma Phys. Control. Fusion, 034001(2019).
[17] P. Mora. Phys. Rev. Lett., 90, 185002(2003).
[18] Y. Takagi, N. Iwata, E. D’Humieres, Y. Sentoku. Phys. Rev. Res., 3, 043140(2021).
[19] C. M. S. Sears, A. Buck, K. Schmid, J. Mikhailova, F. Krausz, L. Veisz. Phys. Rev. Spec. Top. Accel. Beams, 13, 092803(2010).
[20] A. Cianchi, D. Alesini, M. P. Anania, A. Bacci, M. Bellaveglia, M. Castellano, E. Chiadroni, D. Di Giovenale, G. P. Di Pirro, M. Ferrario, A. Gallo, L. Innocenti, A. Mostacci, R. Pompili, A. R. Rossi, J. Scifo, V. Shpakov, C. Vaccarezza, F. Villa. Phys. Rev. Spec. Topic. Accel. Beams, 18, 082804(2015).
[21] V. Shpakov, M. P. Anania, M. Behtouei, M. Bellaveglia, A. Biagioni, M. Cesarini, E. Chiadroni, A. Cianchi, G. Costa, M. Croia, A. Del Dotto, M. Diomede, F. Dipace, M. Ferrario, M. Galletti, A. Giribono, A. Liedl, V. Lollo, L. Magnisi, A. Mostacci, G. Di Pirro, L. Piersanti, R. Pompili, S. Romeo, A. R. Rossi, J. Scifo, C. Vaccarezza, F. Villa, A. Zigler. Phys. Rev. Accel. Beams, 24, 051301(2021).
[22] S. Mondal, I. Chakraborty, S. Ahmad, D. Carvalho, P. Singh, A. D. Lad, V. Narayanan, P. Ayyub, G. R. Kumar, J. Zheng, Z. M. Sheng. Phys. Rev. B, 83, 035408(2011).
[23] G. Cristoforetti, P. Londrillo, P. K. Singh, F. Baffigi, G. D’Arrigo, A. D. Lad, R. G. Milazzo, A. Adak, M. Shaikh, D. Sarkar, G. Chatterjee, J. Jha, M. Krishnamurthy, G. R. Kumar, L. A. Gizzi. Sci. Rep., 7, 1479(2017).
[24] R. Xie, L. H. Cao, Y. Chao, Y. Jiang, Z. J. Liu, C. Y. Zheng, X. T. He. Phys. Plasmas, 27, 123108(2020).
[25] E. Eftekhari-Zadeh, M. S. Blümcke, Z. Samsonova, R. Loetzsch, I. Uschmann, M. Zapf, C. Ronning, O. N. Rosmej, D. Kartashov, C. Spielmann. Phys. Plasmas, 29, 013301(2022).
[26] J. J. Rocca, M. G. Capeluto, R. C. Hollinger, S. Wang, Y. Wang, G. R. Kumar, A. D. Lad, A. Pukhov, V. N. Shlyaptsev. Optica, 11, 437(2024).
[27] P. K. Singh, G. Chatterjee, A. D. Lad, A. Adak, S. Ahmed, M. Khorasaninejad, M. M. Adachi, K. S. Karim, S. S. Saini, A. K. Sood, G. R. Kumar. Appl. Phys. Lett., 100, 244104(2012).
[28] S. Jiang, L. L. Ji, H. Audesirk, K. M. George, J. Snyder, A. Krygier, P. Poole, C. Willis, R. Daskalova, E. Chowdhury, N. S. Lewis, D. W. Schumacher, A. Pukhov, R. R. Freeman, K. U. Akli. Phys. Rev. Lett., 116, 085002(2016).
[29] D. Khaghani, M. Lobet, B. Borm, L. Burr, F. Gärtner, L. Gremillet, L. Movsesyan, O. Rosmej, M. E. Toimil-Molares, F. Wagner, P. Neumayer. Sci. Rep., 7, 11366(2017).
[30] A. Moreau, R. Hollinger, C. Calvi, S. Wang, Y. Wang, M. G. Capeluto, A. Rockwood, A. Curtis, S. Kasdorf, V. N. Shlyaptsev, V. Kaymak, A. Pukhov, J. J. Rocca. Plasma Phys. Control. Fusion, 62, 014013(2020).
[31] S. Jiang, A. G. Krygier, D. W. Schumacher, K. U. Akli, R. R. Freeman. Phys. Rev. E, 89, 013106(2014).
[32] Z. Zhao, L. Cao, L. Cao, J. Wang, W. Huang, W. Jiang, Y. He, Y. Wu, B. Zhu, K. Dong, Y. Ding, B. Zhang, Y. Gu, M. Y. Yu, X. T. He. Phys. Plasmas, 17, 123108(2010).
[33] Y. Yamazaki, T. Kurihara, H. Kobayashi, I. Sato, A. Asami. Nucl. Instrum. Methods Phys. Res., Sect. A, 322, 139(1992).
[34] M. Zhang. , “Emittance formula for slits and pepper-pot measurement”, FERMILAB-TM-1998 ().(1996).
[35] L. A. Gizzi, L. Labate, F. Baffigi, F. Brandi, G. Bussolino, L. Fulgentini, P. Köster, D. Palla. High Power Laser Sci. Eng., 9, e10(2021).
[36] D. Calestani, M. Villani, G. Cristoforetti, F. Brandi, P. Köster, L. Labate, L. A. Gizzi. Matter Radiat. Extremes, 6, 046903(2021).
[37] G. Cristoforetti, A. Anzalone, F. Baffigi, G. Bussolino, G. D’Arrigo, L. Fulgentini, A. Giulietti, P. Köster, L. Labate, S. Tudisco, L. A. Gizzi. Plasma Phys. Control. Fusion, 56, 095001(2014).
[38] T. D. Arber, K. Bennett, C. S. Brady, A. Lawrence-Douglas, M. G. Ramsay, N. J. Sircombe, P. Gillies, R. G. Evans, H. Schmitz, A. R. Bell, C. P. Ridgers. Plasma Phys. Control. Fusion, 57, 113001(2015).
[39] S. C. Wilks, W. L. Kruer, M. Tabak, A. B. Langdon. Phys. Rev. Lett., 69, 1383(1992).
[40] M. Sherlock. Phys. Plasmas, 16, 103101(2009).
[41] A. Macchi. Phys. Plasmas, 25, 031906(2018).
[42] G. Cristoforetti, F. Baffigi, F. Brandi, G. D’Arrigo, A. Fazzi, L. Fulgentini, D. Giove, P. Köster, L. Labate, G. Maero, D. Palla, M. Romé, R. Russo, D. Terzani, P. Tomassini, L. A. Gizzi. Plasma Phys. Control. Fusion, 62, 114001(2020).
[43] L. A. Gizzi, G. Cristoforetti, F. Baffigi, F. Brandi, G. D’Arrigo, A. Fazzi, L. Fulgentini, D. Giove, P. Köster, L. Labate, G. Maero, D. Palla, M. Romé, M. Russo, D. Terzani, P. Tomassini. Phys. Rev. Res., 2, 033451(2020).
[44] G. Chatterjee, P. K. Singh, S. Ahmed, A. P. L. Robinson, A. D. Lad, S. Mondal, V. Narayanan, I. Srivastava, N. Koratkar, J. Pasley, A. K. Sood, G. R. Kumar. Phys. Rev. Lett., 108, 235005(2012).
[45] D. B. Zou, D. Y. Yu, X. R. Jiang, M. Y. Yu, Z. Y. Chen, H. B. Zhuo, C. T. Zhou, S. C. Ruan. Phys. Plasmas, 26, 123105(2019).
[46] Y. Ji, G. Jiang, W. Wu, C. Wang, Y. Gu, Y. Tang. Appl. Phys. Lett., 96, 041504(2010).
[47] Y. Tian, J. Liu, W. Wang, C. Wang, X. Lu, Y. Leng, X. Liang, R. Li, Z. Xu. Plasma Phys. Control. Fusion, 56, 075021(2014).
[48] L. Fedeli, A. Formenti, L. Cialfi, A. Pazzaglia, M. Passoni. Sci. Rep., 8, 3834(2018).
[49] J. Wang, Z. Q. Zhao, W. H. He, L. H. Cao, K. G. Dong, Y. C. Wu, B. Zhu, T. K. Zhang, B. Zhang, Z. M. Zhang, Y. Q. Gu. Phys. Plasmas, 103111(2014).
[50] L. A. Gizzi, A. J. Mackinnon, D. Riley, S. M. Viana, O. Willi. Laser Particle Beams, 13, 511(1995).
[51] G. Sarri, A. Macchi, C. A. Cecchetti, S. Kar, T. V. Liseykina, X. H. Yang, M. E. Dieckmann, J. Fuchs, M. Galimberti, L. A. Gizzi, R. Jung, I. Kourakis, J. Osterholz, F. Pegoraro, A. P. L. Robinson, L. Romagnani, O. Willi, M. Borghesi. Phys. Rev. Lett., 109, 205002(2012).
[52] B. Albertazzi, S. N. Chen, P. Antici, J. Böker, M. Borghesi, J. Breil, V. Dervieux, J. L. Feugeas, L. Lancia, M. Nakatsutsumi, Ph. Nicolai, L. Romagnagni, R. Shepherd, Y. Sentoku, M. Starodubtsev, M. Swantusch, V. T. Tikhonchuk, O. Willi, E. d’Humières, H. Pépin, J. Fuchs. Phys. Plasmas, 22, 123108(2015).
[53] M. Nakatsutsumi, Y. Sentoku, A. Korzhimanov, S. N. Chen, S. Buffechoux, A. Kon, B. Atherton, P. Audebert, M. Geissel, L. Hurd, M. Kimmel, P. Rambo, M. Schollmeier, J. Schwarz, M. Starodubtsev, L. Gremillet, R. Kodama, J. Fuchs. Nat. Commun., 9, 280(2018).
[54] Y. Sakagami, H. Kawakami, S. Nagao, C. Yamanaka. Phys. Rev. Lett., 42, 839(1979).
[55] P. Kolodner, E. Yablonovitch. Phys. Rev. Lett., 43, 1402(1979).
[56] A. Pukhov. Phys. Rev. Lett., 86, 3562(2001).
[57] W. Schumaker, N. Nakanii, C. McGuffey, C. Zulick, V. Chyvkov, F. Dollar, H. Habara, G. Kalintchenko, A. Maksimchuk, K. A. Tanaka, A. G. R. Thomas, V. Yanovsky, K. Krushelnick. Phys. Rev. Lett., 110, 015003(2013).
Get Citation
Copy Citation Text
E. J. Hume, P. Köster, F. Baffigi, F. Brandi, D. Calestani, G. Cristoforetti, L. Fulgentini, L. Labate, A. Marasciulli, S. Morris, D. Palla, M. Salvadori, M. Villani, L. A. Gizzi, K. L. Lancaster. An investigation of the emittance of escaping fast electron beams from planar and nanowire targets[J]. High Power Laser Science and Engineering, 2025, 13(2): 02000e14
Category: Research Articles
Received: Sep. 17, 2024
Accepted: Dec. 31, 2024
Posted: Jan. 3, 2025
Published Online: Apr. 11, 2025
The Author Email: E. J. Hume (emmajane.hume@ino.cnr.it)
CSTR:32185.14.hpl.2025.5







 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence

