The investigation of strong-field quantum electrodynamics (SF-QED) processes requires extreme field intensities approaching the Schwinger limit[1], which cannot be reached by state-of-the-art laser facilities. However, when a relativistic electron travels through an existing intense laser field, the field experienced by the electron in its rest frame is Lorentz transformed to a level where SF-QED effects matter. Therefore, relativistic electrons can act as probes to test these effects. This interaction is known as Thomson or Compton scattering, depending on whether the process is elastic or inelastic scattering. During the scattering, collimated X-/gamma-rays are generated and can be used as radiation sources, commonly known as the inverse Compton scattering (ICS) source. Previously, scattering experiments were conducted in the laboratories of particle accelerators, but the remarkable advances in laser wakefield acceleration (LWFA)[2] have now enabled the study of these experiments under the all-optical setup within high-intensity laser laboratories. The principle of the scattering process is shown in Figure 1.
High Power Laser Science and Engineering, Volume. 13, Issue 4, 04000e56(2025)
A platform for all-optical Thomson/Compton scattering with versatile parameters
A dual-beam platform is developed for all-optical Thomson/Compton scattering, with versatile parameter tuning capabilities including electron energy, radiation energy, radiation polarization, etc. By integrating this platform with a 200 TW Ti:sapphire laser system, we demonstrate the generation of inverse Compton scattering X-/gamma-rays with tunable energies ranging from tens of keV to MeV. The polarization of X-/gamma-rays is manipulated by adjusting the polarization of the scattering laser. In the near future, by combining this platform with multi-PW laser facilities, our goal is to explore the transition from nonlinear Thomson scattering to nonlinear Compton scattering, ultimately verifying theories related to strong-field quantum electrodynamics effects induced by extreme scattering.
1 Introduction
![]()
Figure 1.Schematic diagram of the Thomson/Compton scattering process. A relativistic electron beam collides with a scattering laser. The electrons oscillate and emit X-/gamma-rays. Here, 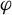 denotes the collision angle between the laser and the electron beam,
denotes the collision angle between the laser and the electron beam, 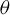 represents the radiation observation angle,
represents the radiation observation angle, 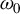 signifies the central frequency of the scattering laser photon and
signifies the central frequency of the scattering laser photon and 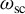 corresponds to the frequency of the emitted photon.
corresponds to the frequency of the emitted photon.
There are two possible configurations for all-optical scattering experiments. One is a simplified version that involves only one laser beam. This laser beam first drives a wakefield accelerator, and then its leftover energy is reflected by a plasma mirror[3–10] onto electrons, causing head-on scattering. The other scheme features a layout with two independently tunable laser pulses[5,11–18]. Although precise temporal and spatial synchronization between the two beamlines is technically difficult, the dual-beam scheme offers the distinct advantage of independently controlling the properties of the scattering process. Each of the two lasers can be individually tuned to optimal conditions, enabling the generation of high-energy electrons and a scattering laser that meets specific requirements, respectively. Specifically, by keeping the parameters of the LWFA constant, one can exclusively manipulate the colliding pulse, enabling a single-variable investigation into the scattering process.
To investigate these scattering processes, we established an experimental platform for dual-beam all-optical Thomson/Compton scattering (EPATCS) with versatile parameter tuning capabilities. The EPATCS is a tabletop electron–photon interaction setup, where high-energy electrons are accelerated by one laser beam and then collide with the second laser beam. The flexibility in parameter tuning not only enhances control over experimental conditions, but also opens up new prospects for investigating high-field scattering processes. By precisely controlling the intensity, polarization state and field mode of the colliding laser beam, we can generate X-/gamma-rays with varying characteristics, which can serve as light sources for applications such as high-density dynamic imaging[19–26] and vortex photons for photonuclear physics[27,28]. The EPATCS can also be built on PW laser facilities and provides the possibility of interaction between multi-GeV electrons and high laser intensity under extreme conditions[18] to study SF-QED effects, including the radiation reaction[11,12], pair production[10,29–31], conversion of angular momentum transfer in the collision process[32–34], etc.
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
This paper is organized as follows. In Section 2, we discuss the versatile tuning of ICS X-/gamma-ray source parameters and their impact on enhancing control over high-field processes and tunable radiation spectra. Section 3 presents the experimental results based on the EPATCS at the 200 TW laser of Shanghai Jiao Tong University. In Section 4, we elucidate the prospective SF-QED research of the EPATCS.
2 Versatile tuning parameters of the experimental platform for dual-beam all-optical Thomson/Compton scattering
The EPATCS offers the potential for multi-parameter adjustments, including tuning the electron beam energy, altering the collision angle between electrons and photons and adjusting the parameters of the colliding laser (such as the laser intensity, wavelength, polarization and orbital angular momentum). In this section, we introduce the experimental designs and explorations to investigate the adjustable parameters and their effects on radiation.
A schematic diagram of a dual-beam collision layout is as shown in Figure 2(a), to investigate the influence of multiple parameters on the photon energy of radiation in the ICS process. The combination of the optical system and guide rail enables precise adjustments to the electron–laser collision angle. Adjustments in the collision angle
![]()
Figure 2.(a) Schematic diagram of the experimental layout with multiple collision angles. (b) Radiation energy under different collision angles 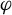 with electron energy from 100 MeV (blue) to 300 MeV (red) when the observed angle
with electron energy from 100 MeV (blue) to 300 MeV (red) when the observed angle 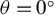 . The cases of
. The cases of 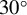 and
and 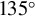 are specifically marked to correspond with the experimental results discussed later in Section
are specifically marked to correspond with the experimental results discussed later in Section
To illustrate this principle with a specific example, adjusting the collision angle demonstrates how changes in laser parameters can regulate radiation. In the ICS process, altering the collision angle between electrons and photons can significantly modify the energy spectrum of the emitted radiation. The energy of the emitted photon
In Section 3, the collision angle
3 X-/gamma-ray manipulation by the experimental platform for dual-beam all-optical Thomson/Compton scattering on a 200 TW laser
To validate the applicability of the EPATCS, it was initially integrated into the 200 TW Ti:sapphire laser facility at the Key Laboratory for Laser Plasmas of Shanghai Jiao Tong University. A 5 J p-polarized laser pulse with a duration of
3.1 Energy tunability of X-/gamma-rays via LWFA electrons
The laser pulse for LWFA is focused by an off-axis parabolic (OAP) mirror of F# 20 to a Gaussian-like spot size, containing 30% energy with an FWHM diameter of 26 μm, and the focused laser intensity can reach up to
As shown in Figure 3, consistent energy electron beams, tunable within the range of 200–600 MeV, can be achieved under stable conditions. For each scenario, the plasma density and acceleration length are indicated, resulting in relatively stable electron energy spectra. Under appropriate plasma density, decreasing the acceleration length within a certain range can effectively enhance the energy of relativistic electrons. The corresponding electron spectrum is shown in Figures 3(a)–3(d). However, as shown in Figures 3(d) and 3(e), when the plasma density is significantly increased, the phase velocity of the wakefield decreases, causing the electrons to dephase earlier, leading to a reduction in their energy. Based on the scale shown in Figure 3 and the actual distance of the image plate from the target, which is 1.6 m, the transverse divergence angle of the electron bunch is approximately 3 mrad (FWHM).
![]()
Figure 3.Diagnosis results of the electron beam with different acceleration lengths or plasma densities. From (a) to (e), the corresponding plasma densities are 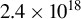 ,
, 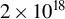 ,
, 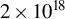 ,
, 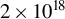 and
and 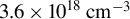 , respectively, with acceleration lengths of 10, 9.5, 9, 8 and 8 mm.
, respectively, with acceleration lengths of 10, 9.5, 9, 8 and 8 mm.
The tuning energy of the electron enables the radiation energy spectrum to span a wide range. As indicated in Equation (1), when
3.2 Energy control of X-/gamma-rays by the interaction angle
In the scattering experiments, the relativistic electrons generated by LWFA have a cut-off energy of approximately 300 MeV, approaching a continuous spectrum. Two experimental configurations with collision angles of
![]()
Figure 4.(a), (b) Experimental layout diagrams of AOICS under two conditions of 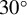 and
and 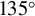 collision angles, respectively. (c), (d) Radiation spectra with error bars for collision angles of
collision angles, respectively. (c), (d) Radiation spectra with error bars for collision angles of 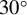 and
and 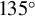 , respectively. The corresponding electron energy spectrum for each instance is displayed in the upper right-hand corner of each graph.
, respectively. The corresponding electron energy spectrum for each instance is displayed in the upper right-hand corner of each graph.
![]()
Figure 5.(a) Experimental layout. The polarization state of the X-ray was obtained by placing the polyethylene (PE) forward in the X-ray and placing four image plates around it to diagnose the signal scattering in different polarization states. (b) Schematic representation of Compton scattering of linearly/circularly polarized X-rays with PE scatterers. The red portions indicate the distribution direction of the scattered electrons. (c), (d) Simulation results by FLUKA software, corresponding to the respective Compton scattering signals of linearly polarized and circularly polarized X-rays with PE. (e), (f) Experimental diagnostic results of linearly polarized and circularly polarized X-rays, respectively. (g), (h) The signal image formed by black dots is the one-dimensional integral result of the experimental results, while the dashed blue line represents the simulation results.
In the experimental setup with a collision angle of
In the case of a collision angle of
3.3 Polarization control of X-/gamma-rays
Polarized X-rays can be used to probe the characteristics of magnetic structures in structural magnetism and distinguish between chiral and helical magnetic structures[40–44]. Based on the EPATCS, we generate polarized X-rays via the collision of a polarized laser beam and the electrons. As shown in Figure 5(a), a half-wave plate or a quarter-wave plate is incorporated into the scattering laser path to change the polarization state of the scattering laser, which in turn modifies the polarization state of the generated radiation. An OAP mirror of F# 5 is used to focus the colliding laser. Under linear polarization conditions, the focal spot diameter and laser intensity are the same as those presented in Section 3.2, whereas under circular polarization, the laser intensity is approximately
As shown in Figure 5(a), a cylindrical polyethylene converter with a diameter of 2 cm and a length of 15 cm is placed 1.9 m from the impact point, and four image plates are placed around the converter. The secondary photon signal radiated on the scatterer is diagnosed in the vertical direction of X-ray propagation based on the Compton scattering. When the scattering angle is close to
We conducted simulations using FLUKA software to simulate the process; the results are shown in Figures 5(c) and 5(d) and the experimental results are shown in Figures 5(e) and 5(f). Each result accumulated 100 shots, which facilitated the diagnosis of the polarization characteristics of the radiation through the scattered electron distribution. The four image plates are arranged to correspond to azimuth angles ranging from
The aforementioned experimental results demonstrate precise control over electron energy, with a wide range of radiation energy and polarization states. These verify the versatile multiparameter tunability of the EPATCS. In our platform, the pulse duration of the electron bunch generated by LWFA is typically a few femtoseconds[47], and the laser pulse duration is 25 fs. Therefore, in order to realize the collision process described in Sections 3.2 and 3.3, following the approaches outlined in previous works[48,49], we implemented spatial and temporal synchronization, achieved measured time jitters below 10 fs and maintained a high spatial accuracy of electron–photon collisions within 5 μm. Moreover, our experimental results confirm that this level of precision is essential for stable electron–laser collisions.
4 Prospective roadmap for strong-field quantum electrodynamics research via the experimental platform for dual-beam all-optical Thomson/Compton scattering
By integrating with multi-PW laser facilities, the adjustable parameters of the EPATCS provide a fundamental platform for the approaching research initiatives, including multiphoton Thomson/Compton scattering, radiation reaction, vacuum polarization effects and pair production[45,50–55]. When high-energy electrons interact with an intense laser, and the laser intensity in the rest frame of the electron approaches or reaches the Schwinger critical field

Table 1. The fundamental experimental proposal and parameters.
Table 1. The fundamental experimental proposal and parameters.
Fundamental experimental proposal Electron energy $\gamma$ Normalized intensity ${a}_0$ Quantum parameter ${\chi}_\mathrm{e}$ Phase I From linear to nonlinear regime of ICS; precision experiment of radiation reaction $\lesssim 2000$ 20 $\lesssim 0.2$ Phase II Research of CRDR for Compton scattering $\sim 4000$ $40\text{--}60$ $\sim 1$ Phase III Research of QRDR for Compton scattering and the nonlinear Breit--Wheeler process $\gtrsim 4000$ $\sim 200$ $\gtrsim \mathrm{4}$
In phase I, the EPATCS will be transferred and built in multiple advanced laser facilities. The platform will be transferred to the 0.5 PW femtosecond laser facility, which is commissioned in the Key Laboratory for Laser Plasmas at Shanghai Jiao Tong University. According to the matching condition of the LWFA, a low-energy dispersive electron beam with a maximum energy of less than 1 GeV can be generated stably. Another focused laser beam with an intensity of up to
In phase II, the platform will be transferred to PW-level laser facilities, for instance, on a 1 PW laser facility at the Synergetic Extreme Condition User Facility (SECUF) of the Institute of Physics in the Chinese Academy of Sciences. It can contribute to studies of the classical radiation-dominated regime (CRDR)[54,55] with normalized amplitude
In phase III, the EPATCS could be transferred to 10 PW laser facilities, such as SULF[62], SEL[63], APOLLON[64], ELI[65,66] and EP-OPAL[67]. Considering that a stable electron energy of multi-GeV could be generated, the normalized amplitude
![]()
Figure 6.The relevant international experimental progress and proposals[3–6,11–17,71–80]. The solid-colored sections represent experiments that have been completed or are currently being planning, while the hollow elliptical regions correspond to the parameter ranges associated with the three phases discussed in this paper. The ranges corresponding to the classical radiation-dominated regime (CRDR) and the quantum radiation-dominated regime (QRDR) are indicated.
5 Conclusions
The development of an all-optical Thomson/Compton scattering platform, the EPATCS, featuring versatile parameter tunability, harnesses the exceptional benefits of LWFA and super-intense ultrafast lasers. We successfully demonstrate the capability of the EPATCS by providing precise control over the parameters of the X-rays of ICS, including the energy spectrum, polarization state and other parameters of high-energy radiation. With the ongoing development of super-intense ultrafast laser facilities, we aim to explore SF-QED in depth under various physical regimes, including radiation damping, nonlinear Compton scattering and nonlinear Breit–Wheeler electron–positron pair production.
Principle of X-/gamma-ray spectrum diagnostics
Due to differences in X-ray energy resulting from collisions at different angles, two diagnostic approaches are implemented.
In the ICS experiment with a collision angle of
![]()
Figure 7.(a) The signal intensity distribution on the image plate in the 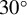 collision angle ICS experiment, along with the corresponding types of metal filters and their respective thicknesses. (b) The transmission curves for different energy intervals are obtained by subtracting the transmission rates of adjacent filter combinations, where the annotated numbers correspond to the numbers in (a).
collision angle ICS experiment, along with the corresponding types of metal filters and their respective thicknesses. (b) The transmission curves for different energy intervals are obtained by subtracting the transmission rates of adjacent filter combinations, where the annotated numbers correspond to the numbers in (a).
![]()
Figure 8.(a) The signal intensity distribution on the image plate in the 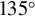 collision angle ICS experiment, along with the corresponding types of metal filters and their respective thicknesses. (b) The radiation transmittance curves of different metal filters varying with energy.
collision angle ICS experiment, along with the corresponding types of metal filters and their respective thicknesses. (b) The radiation transmittance curves of different metal filters varying with energy.
![]()
Figure 9.The overlap geometry of the experimental schematic diagram.
Based on the electron spectrum, the corresponding gamma-ray spectrum can be calculated as a reference spectrum. Within the energy range of the reference spectrum, the gamma-ray reference spectra are discretized by selecting evenly spaced energy reference points
With this evaluation function, multiple iterative calculations are performed and the iterative function is as follows[
The iteration proceeds until the variance minimizes, at which point the process concludes, yielding the final radiation spectrum. The errors mainly arise from the numerical fluctuations in signal intensity across various regions of the experimental results.
The experimental schematic diagram
The primary components of the experiment include two laser beams, a gas nozzle and diagnostic systems for both electrons and radiation, as shown in
For energy spectrum measurements, filters are added between the magnet and CsI to perform radiation spectrum diagnostics. When the radiation energy is of the order of tens of keV or lower, an image plate is used instead of the CsI scintillator to image the radiation profile. For polarization measurements, a cylindrical plastic converter is placed after the electron deflection, along with four image plates positioned perpendicular to each other.
[1] J. Schwinger. Phys. Rev., 82, 664(1951).
[2] T. Tajima, J. M. Dawson. Phys. Rev. Lett., 43, 267(1979).
[3] K. Ta Phuoc, S. Corde, C. Thaury, V. Malka, A. Tafzi, J. P. Goddet, R. C. Shah, S. Sebban, A. Rousse. Nat. Photonics, 6, 308(2012).
[4] H.-E. Tsai, X. Wang, J. M. Shaw, Z. Li, A. V. Arefiev, X. Zhang, R. Zgadzaj, W. Henderson, V. Khudik, G. Shvets, M. C. Downer. Phys. Plasmas, 22, 023106(2015).
[5] C. Yu, R. Qi, W. Wang, J. Liu, W. Li, C. Wang, Z. Zhang, J. Liu, Z. Qin, M. Fang, K. Feng, Y. Wu, Y. Tian, Y. Xu, F. Wu, Y. Leng, X. Weng, J. Wang, F. Wei, Y. Yi, Z. Song, R. Li, Z. Xu. Sci. Rep., 6, 29518(2016).
[6] A. Döpp, E. Guillaume, C. Thaury, J. Gautier, I. Andriyash, A. Lifschitz, V. Malka, A. Rousse, K. T. Phuoc. Plasma Phys. Control. Fusion, 58, 034005(2016).
[7] C. Zhu, J. Wang, J. Feng, Y. Li, D. Li, M. Li, Y. He, J. Ma, J. Tan, B. Zhang, W. Yan, L. Chen. Plasma Phys. Control. Fusion, 61, 024001(2019).
[8] Y. Wu, C. Yu, Z. Qin, W. Wang, R. Qi, Z. Zhang, K. Feng, L. Ke, Y. Chen, C. Wang, J. Liu, R. Li, Z. Xu. Plasma Phys. Control. Fusion, 61, 085030(2019).
[9] Y. Ma, J. Hua, D. Liu, Y. He, T. Zhang, J. Chen, F. Yang, X. Ning, H. Zhang, Y. Du, W. Lu. Phys. Rev. Appl., 19, 014073(2023).
[10] Y.-J. Gu, S. Weber. Opt. Express, 26, 19932(2018).
[11] J. M. Cole, K. T. Behm, E. Gerstmayr, T. G. Blackburn, J. C. Wood, C. D. Baird, M. J. Duff, C. Harvey, A. Ilderton, A. S. Joglekar, K. Krushelnick, S. Kuschel, M. Marklund, P. McKenna, C. D. Murphy, K. Poder, C. P. Ridgers, G. M. Samarin, G. Sarri, D. R. Symes, A. G. R. Thomas, J. Warwick, M. Zepf, Z. Najmudin, S. P. D. Mangles. Phys. Rev. X, 8, 011020(2018).
[12] K. Poder, M. Tamburini, G. Sarri, A. Di Piazza, S. Kuschel, C. D. Baird, K. Behm, S. Bohlen, J. M. Cole, D. J. Corvan, M. Duff, E. Gerstmayr, C. H. Keitel, K. Krushelnick, S. P. D. Mangles, P. McKenna, C. D. Murphy, Z. Najmudin, C. P. Ridgers, G. M. Samarin, D. R. Symes, A. G. R. Thomas, J. Warwick, M. Zepf. Phys. Rev. X, 8, 031004(2018).
[13] N. D. Powers, I. Ghebregziabher, G. Golovin, C. Liu, S. Chen, S. Banerjee, J. Zhang, D. P. Umstadter. Nat. Photonics, 8, 28(2014).
[14] S. Chen, N. D. Powers, I. Ghebregziabher, C. M. Maharjan, C. Liu, G. Golovin, S. Banerjee, J. Zhang, N. Cunningham, A. Moorti, S. Clarke, S. Pozzi, D. P. Umstadter. Phys. Rev. Lett., 110, 155003(2013).
[15] C. Liu, G. Golovin, S. Chen, J. Zhang, B. Zhao, D. Haden, S. Banerjee, J. Silano, H. Karwowski, D. Umstadter. Opt. Lett., 39, 4132(2014).
[16] K. Khrennikov, J. Wenz, A. Buck, J. Xu, M. Heigoldt, L. Veisz, S. Karsch. Phys. Rev. Lett., 114, 195003(2015).
[17] W. Yan, C. Fruhling, G. Golovin, D. Haden, J. Luo, P. Zhang, B. Zhao, J. Zhang, C. Liu, M. Chen, S. Chen, S. Banerjee, D. Umstadter. Nat. Photonics, 11, 514(2017).
[18] A. Pukhov, J. Meyer-ter Vehn. Appl. Phys. B Lasers Opt., 74, 355(2002).
[19] L. B. Fletcher, H. J. Lee, T. Döppner, E. Galtier, B. Nagler, P. Heimann, C. Fortmann, S. LePape, T. Ma, M. Millot, A. Pak, D. Turnbull, D. A. Chapman, D. O. Gericke, J. Vorberger, T. White, G. Gregori, M. Wei, B. Barbrel, R. W. Falcone, C.-C. Kao, H. Nuhn, J. Welch, U. Zastrau, P. Neumayer, J. B. Hastings, S. H. Glenzer. Nat. Photonics, 9, 274(2015).
[20] T. Gorkhover, S. Schorb, R. Coffee, M. Adolph, L. Foucar, D. Rupp, A. Aquila, J. D. Bozek, S. W. Epp, B. Erk, L. Gumprecht, L. Holmegaard, A. Hartmann, R. Hartmann, G. Hauser, P. Holl, A. Hömke, P. Johnsson, N. Kimmel, K.-U. Kühnel, M. Messerschmidt, C. Reich, A. Rouzée, B. Rudek, C. Schmidt, J. Schulz, H. Soltau, S. Stern, G. Weidenspointner, B. White, J. Küpper, L. Strüder, I. Schlichting, J. Ullrich, D. Rolles, A. Rudenko, T. Möller, C. Bostedt. Nat. Photonics, 10, 93(2016).
[21] A. Schropp, R. Hoppe, V. Meier, J. Patommel, F. Seiboth, Y. Ping, D. G. Hicks, M. A. Beckwith, G. W. Collins, A. Higginbotham, J. S. Wark, H. J. Lee, B. Nagler, E. C. Galtier, B. Arnold, U. Zastrau, J. B. Hastings, C. G. Schroer. Sci. Rep., 5, 11089(2015).
[22] T. Kluge, C. Rödel, M. Rödel, A. Pelka, E. E. McBride, L. B. Fletcher, M. Harmand, A. Krygier, A. Higginbotham, M. Bussmann, E. Galtier, E. Gamboa, A. L. Garcia, M. Garten, S. H. Glenzer, E. Granados, C. Gutt, H. J. Lee, B. Nagler, W. Schumaker, F. Tavella, M. Zacharias, U. Schramm, T. E. Cowan. Phys. Plasmas, 24, 102709(2017).
[23] T. Kluge, M. Rödel, J. Metzkes-Ng, A. Pelka, A. L. Garcia, I. Prencipe, M. Rehwald, M. Nakatsutsumi, E. E. McBride, T. Schönherr, M. Garten, N. J. Hartley, M. Zacharias, J. Grenzer, A. Erbe, Y. M. Georgiev, E. Galtier, I. Nam, H. J. Lee, S. Glenzer, M. Bussmann, C. Gutt, K. Zeil, C. Rödel, U. Hübner, U. Schramm, T. E. Cowan. Phys. Rev. X, 8, 031068(2018).
[24] M. Mo, S. Murphy, Z. Chen, P. Fossati, R. Li, Y. Wang, X. Wang, S. Glenzer. Sci. Adv., 5, eaaw0392(2019).
[25] L. Gaus, L. Bischoff, M. Bussmann, E. Cunningham, C. B. Curry, J. E, E. Galtier, M. Gauthier, A. L. García, M. Garten, S. Glenzer, J. Grenzer, C. Gutt, N. J. Hartley, L. Huang, U. Hübner, D. Kraus, H. J. Lee, E. E. McBride, J. Metzkes-Ng, B. Nagler, M. Nakatsutsumi, J. Nikl, M. Ota, A. Pelka, I. Prencipe, L. Randolph, M. Rödel, Y. Sakawa, H.-P. Schlenvoigt, M. Šmíd, F. Treffert, K. Voigt, K. Zeil, T. E. Cowan, U. Schramm, T. Kluge. Phys. Rev. Res., 3, 043194(2021).
[26] Y. Wu, S. Wang, B. Zhu, Y. Yan, M. Yu, G. Li, X. Zhang, Y. Yang, F. Tan, F. Lu, B. Bi, X. Mao, Z. Wang, Z. Zhao, J. Su, W. Zhou, Y. Gu. Matter Radiat. Extremes, 9, 037202(2024).
[27] D. Habs, T. Tajima, J. Schreiber, C. P. J. Barty, M. Fujiwara, P. G. Thirolf. Eur. Phys. J. D, 55, 279(2009).
[28] H. A. Weidenmüller. Phys. Rev. Lett., 106, 122502(2011).
[29] G. Breit, J. A. Wheeler. Phys. Rev., 46, 1087(1934).
[30] H. R. Reiss. J. Math. Phys., 3, 59(1962).
[31] Y.-J. Gu, O. Klimo, S. V. Bulanov, S. Weber. Commun. Phys., 1, 93(2018).
[32] V. Petrillo, G. Dattoli, I. Drebot, F. Nguyen. Phys. Rev. Lett., 117, 123903(2016).
[33] Y.-Y. Chen, J.-X. Li, K. Z. Hatsagortsyan, C. H. Keitel. Phys. Rev. Lett., 121, 074801(2018).
[34] M. Ababekri, R.-T. Guo, F. Wan, B. Qiao, Z. Li, C. Lv, B. Zhang, W. Zhou, Y. Gu, J.-X. Li. Phys. Rev. D, 109, 016005(2024).
[35] A. Döpp, K. T. Phuoc, I. A. Andriyash. J. Plasma Phys., 89, 965890501(2023).
[36] W. Zhou, W. Yan, J. Wang, L. Chen. Ultrafast Sci., 3, 0005(2023).
[37] A. Debus, S. Bock, M. Bussmann, T. E. Cowan, A. Jochmann, T. Kluge, S. D. Kraft, R. Sauerbrey, K. Zeil, U. Schramm. Proc. SPIE, 7359, 735908(2009).
[38] J. Wenz, A. Döpp, K. Khrennikov, S. Schindler, M. F. Gilljohann, H. Ding, J. Götzfried, A. Buck, J. Xu, M. Heigoldt, W. Helml, L. Veisz, S. Karsch. Nat. Photonics, 13, 263(2019).
[39] P.-H. Huang, K. R. Kase, B. E. Bjärngard. Med. Phys., 9, 695(1982).
[40] H. Ohsumi, T.-h. Arima. Adv. Phys. X, 1, 128(2016).
[41] Y. Togawa, Y. Kousaka, K. Inoue, J.-i. Kishine. J. Phys. Soc. Jpn., 85, 112001(2016).
[42] S. L. Zhang, G. Van Der Laan, T. Hesjedal. Phys. Rev. B, 96, 094401(2017).
[43] A. T. Schmitt, Y. Joly, K. S. Schulze, B. Marx-Glowna, I. Uschmann, B. Grabiger, H. Bernhardt, R. Loetzsch, A. Juhin, J. Debray, H.-C. Wille, H. Yavaş, G. G. Paulus, R. Röhlsberger. Optica, 8, 56(2021).
[44] D. P. Siddons, M. Hart, Y. Amemiya, J. B. Hastings. Phys. Rev. Lett., 64, 1967(1990).
[45] G.-P. An, Y.-L. Chi, Y.-L. Dang, G.-Y. Fu, B. Guo, Y.-S. Huang, C.-Y. He, X.-C. Kong, X.-F. Lan, J.-C. Li, F.-L. Liu, J.-S. Shi, X.-J. Sun, Y. Wang, J.-L. Wang, L. Wang, Y.-Y. Wei, G. Wu, G.-L. Xu, X.-F. Xi, G.-J. Yang, C.-L. Zhang, Z. Zhang, Z.-P. Zheng, X.-D. Zhang, S.-P. Zhang. Matter Radiat. Extremes, 3, 219(2018).
[46] G. O. Depaola. Nucl. Instrum. Methods Phys. Res. Sect. A, 512, 619(2003).
[47] O. Lundh, J. Lim, C. Rechatin, L. Ammoura, A. Ben-Ismaïl, X. Davoine, G. Gallot, J.-P. Goddet, E. Lefebvre, V. Malka, J. Faure. Nat. Phys., 7, 219(2011).
[48] D. Y. Kim, C. I. Hojbota, M. Mirzaie, S. K. Lee, K. Y. Kim, J. H. Sung, C. H. Nam. Rev. Sci. Instrum., 93, 113001(2022).
[49] D. J. Corvan, T. Dzelzainis, C. Hyland, G. Nersisyan, M. Yeung, M. Zepf, G. Sarri. Opt. Express, 24, 3127(2016).
[50] A. Gonoskov, T. G. Blackburn, M. Marklund, S. S. Bulanov. Rev. Mod. Phys., 94, 045001(2022).
[51] A. Di Piazza, C. Müller, K. Z. Hatsagortsyan, C. H. Keitel. Rev. Mod. Phys., 84, 1177(2012).
[52] S. Weber, S. Bechet, S. Borneis, L. Brabec, M. Bučka, E. Chacon-Golcher, M. Ciappina, M. DeMarco, A. Fajstavr, K. Falk, E.-R. Garcia, J. Grosz, Y.-J. Gu, J.-C. Hernandez, M. Holec, P. Janečka, M. Jantač, M. Jirka, H. Kadlecova, D. Khikhlukha, O. Klimo, G. Korn, D. Kramer, D. Kumar, T. Lastovička, P. Lutoslawski, L. Morejon, V. Olšovcová, M. Rajdl, O. Renner, B. Rus, S. Singh, M. Šmid, M. Sokol, R. Versaci, R. Vrána, M. Vranic, J. Vyskočil, A. Wolf, Q. Yu. Matter Radiat. Extremes, 2, 149(2017).
[53] Y.-J. Gu, M. Jirka, O. Klimo, S. Weber. Matter Radiat. Extremes, 4, 064403(2019).
[54] A. S. Samsonov, E. N. Nerush, I. Yu. Kostyukov. Matter Radiat. Extremes, 8, 014402(2023).
[55] S. S. Bulanov, C. B. Schroeder, E. Esarey, W. P. Leemans. Phys. Rev. A, 87, 062110(2013).
[56] T. Heinzl, B. King, A. J. MacLeod. Phys. Rev. A, 102, 063110(2020).
[57] A. Di Piazza, M. Tamburini, S. Meuren, C. H. Keitel. Phys. Rev. A, 99, 022125(2019).
[58] M. Kh. Khokonov, H. Nitta. Phys. Rev. Lett., 89, 094801(2002).
[59] A. Ilderton, B. King, D. Seipt. Phys. Rev. A, 99, 042121(2019).
[60] T. Podszus, A. Di Piazza. Phys. Rev. D, 99, 076004(2019).
[61] E. G. Gelfer, A. M. Fedotov, A. A. Mironov, S. Weber. Phys. Rev. D, 106, 056013(2022).
[62] W. Li, Z. Gan, L. Yu, C. Wang, Y. Liu, Z. Guo, L. Xu, M. Xu, Y. Hang, Y. Xu, J. Wang, P. Huang, H. Cao, B. Yao, X. Zhang, L. Chen, Y. Tang, S. Li, X. Liu, S. Li, M. He, D. Yin, X. Liang, Y. Leng, R. Li, Z. Xu. Opt. Lett., 43, 5681(2018).
[63] E. Cartlidge. Science, 359, 382(2018).
[64] K. Burdonov, A. Fazzini, V. Lelasseux, J. Albrecht, P. Antici, Y. Ayoul, A. Beluze, D. Cavanna, T. Ceccotti, M. Chabanis, A. Chaleil, S. N. Chen, Z. Chen, F. Consoli, M. Cuciuc, X. Davoine, J. P. Delaneau, E. d’Humières, J.-L. Dubois, C. Evrard, E. Filippov, A. Freneaux, P. Forestier-Colleoni, L. Gremillet, V. Horny, L. Lancia, L. Lecherbourg, N. Lebas, A. Leblanc, W. Ma, L. Martin, F. Negoita, J.-L. Paillard, D. Papadopoulos, F. Perez, S. Pikuz, G. Qi, F. Quéré, L. Ranc, P.-A. Söderström, M. Scisciò, S. Sun, S. Vallières, P. Wang, W. Yao, F. Mathieu, P. Audebert, J. Fuchs. Matter Radiat. Extremes, 6, 064402(2021).
[65] M. Aléonard, M. Altarelli, P. Antici, A. Apolonskiy, P. Audebert, A. Bartnik, C. Barty, A. Bernstein, J. Biegert, P. Böni, N. Booth, D. Bote, S. Bulanov, R. Butkus, L. Cardoso, J. P. Chambaret, D. Charambilidis, G. Cheriaux, R. Clarke, M. ZepfWHITEBOOK ELI – Extreme Light Infrastructure; Science and Technology with Ultra-Intense Lasers. , , , , , , , , , , , , , , , , , , , and , (Andreas Thoss, ).(2011).
[66] C. Radier, O. Chalus, M. Charbonneau, S. Thambirajah, G. Deschamps, S. David, J. Barbe, E. Etter, G. Matras, S. Ricaud, V. Leroux, C. Richard, F. Lureau, A. Baleanu, R. Banici, A. Gradinariu, C. Caldararu, C. Capiteanu, A. Naziru, B. Diaconescu, V. Iancu, R. Dabu, D. Ursescu, I. Dancus, C. A. Ur, K. A. Tanaka, N. V. Zamfir. High Power Laser Sci. Eng., 10, e21(2022).
[67] J. D. Zuegel, S.-W. Bahk, I. A. Begishev, J. Bromage, C. Dorrer, A. V. Okishev, J. B. Oliver. CLEO: 2014, JTh4L.4(2014).
[68] V. I. Ritus. J. Sov. Laser Res., 6, 497(1985).
[69] A. Di Piazza, K. Z. Hatsagortsyan, C. H. Keitel. Phys. Rev. Lett., 105, 220403(2010).
[70] A. Di Piazza. Lett. Math. Phys., 83, 305(2008).
[71] C. Bula, K. T. McDonald, E. J. Prebys, C. Bamber, S. Boege, T. Kotseroglou, A. C. Melissinos, D. D. Meyerhofer, W. Ragg, D. L. Burke, R. C. Field, G. Horton-Smith, A. C. Odian, J. E. Spencer, D. Walz, S. C. Berridge, W. M. Bugg, K. Shmakov, A. W. Weidemann. Phys. Rev. Lett., 76, 3116(1996).
[72] D. L. Burke, R. C. Field, G. Horton-Smith, J. E. Spencer, D. Walz, S. C. Berridge, W. M. Bugg, K. Shmakov, A. W. Weidemann, C. Bula, K. T. McDonald, E. J. Prebys, C. Bamber, S. J. Boege, T. Koffas, T. Kotseroglou, A. C. Melissinos, D. D. Meyerhofer, D. A. Reis, W. Ragg. Phys. Rev. Lett., 79, 1626(1997).
[73] H. Schwoerer, B. Liesfeld, H.-P. Schlenvoigt, K.-U. Amthor, R. Sauerbrey. Phys. Rev. Lett., 96, 014802(2006).
[74] G. Sarri, D. J. Corvan, W. Schumaker, J. M. Cole, A. Di Piazza, H. Ahmed, C. Harvey, C. H. Keitel, K. Krushelnick, S. P. D. Mangles, Z. Najmudin, D. Symes, A. G. R. Thomas, M. Yeung, Z. Zhao, M. Zepf. Phys. Rev. Lett., 113, 224801(2014).
[75] M. Mirzaie, C. I. Hojbota, D. Y. Kim, V. B. Pathak, T. G. Pak, C. M. Kim, H. W. Lee, J. W. Yoon, S. K. Lee, Y. J. Rhee, M. Vranic, Ó. Amaro, K. Y. Kim, J. H. Sung, C. H. Nam. Nat. Photonics, 18, 1212(2024).
[76] I. C. E. Turcu, F. Negoita, D. A. Jaroszynski, P. Mckenna, S. Balascuta, D. Ursescu, I. Dancus, M. O. Cernaianu, M. V. Tataru, P. Ghenuche, D. Stutman, A. Boianu, M. Risca, M. Toma, C. Petcu, G. Acbas, S. R. Yoffe, A. Noble, B. Ersfeld, E. Brunetti, R. Capdessus, C. Murphy, C. P. Ridgers, D. Neely, S. P. D. Mangles, R. J. Gray, A. G. R. Thomas, J. G. Kirk, A. Ilderton, M. Marklund, D. F. Gordon, B. Hafizi, D. Kaganovich, J. P. Palastro, E. D’Humieres, M. Zepf, G. Sarri, H. Gies, F. Karbstein, J. Schreiber, G. G. Paulus, B. Dromey, C. Harvey, A. Di Piazza, C. H. Keitel, M. C. Kaluza, S. Gales, N. V. Zamfir. Rom. Rep. Phys, 68, S145(2016).
[77] Z. Chen, S. Meuren, E. Gerstmayr, V. Yakimenko, P. H. Bucksbaum, D. A. Reis. Optica High-brightness Sources and Light-driven Interactions Congress 2022, HF4B.6(2022).
[78] H. Abramowicz, M. A. Soto, M. Altarelli, R. Aßmann, A. Athanassiadis, G. Avoni, T. Behnke, M. Benettoni, Y. Benhammou, J. Bhatt, T. Blackburn, C. Blanch, S. Bonaldo, S. Boogert, O. Borysov, M. Borysova, V. Boudry, D. Breton, R. Brinkmann, M. Bruschi, F. Burkart, K. Büßer, N. Cavanagh, F. Dal Corso, W. Decking, M. Deniaud, O. Diner, U. Dosselli, M. Elad, L. Epshteyn, D. Esperante, T. Ferber, M. Firlej, T. Fiutowski, K. Fleck, N. Fuster-Martinez, K. Gadow, F. Gaede, A. Gallas, H. G. Cabrera, E. Gerstmayr, V. Ghenescu, M. Giorato, N. Golubeva, C. Grojean, P. Grutta, G. Grzelak, J. Hallford, L. Hartman, B. Heinemann, T. Heinzl, L. Helary, L. Hendriks, M. Hoffmann, D. Horn, S. Huang, X. Huang, M. Idzik, A. Irles, R. Jacobs, B. King, M. Klute, A. Kropf, E. Kroupp, H. Lahno, F. L. Manghi, J. Lawhorn, A. Levanon, A. Levi, L. Levinson, A. Levy, I. Levy, A. Liberman, B. Liss, B. List, J. List, W. Lohmann, J. Maalmi, T. Madlener, V. Malka, T. Marsault, S. Mattiazzo, F. Meloni, D. Miron, M. Morandin, J. Moroń, J. Nanni, A. T. Neagu, E. Negodin, A. Paccagnella, D. Pantano, D. Pietruch, I. Pomerantz, R. Pöschl, P. M. Potlog, R. Prasad, R. Quishpe, E. Ranken, A. Ringwald, A. Roich, F. Salgado, A. Santra, G. Sarri, A. Sävert, A. Sbrizzi, S. Schmitt, I. Schulthess, S. Schuwalow, D. Seipt, G. Simi, Y. Soreq, D. Spataro, M. Streeter, K. Swientek, N. T. Hod, T. Teter, A. Thiebault, D. Thoden, N. Trevisani, R. Urmanov, S. Vasiukov, S. Walker, M. Warren, M. Wing, Y. C. Yap, N. Zadok, M. Zanetti, A. F. Żarnecki, P. Zbińkowski, K. Zembaczyński, M. Zepf, D. Zerwas, W. Ziegler, M. Zuffa. Eur. Phys. J. Spec. Top., 233, 1709(2024).
[81] I. V. Khutoretsky. Rev. Sci. Instrum., 66, 773(1995).
[82] T. Bonnet, M. Comet, D. Denis-Petit, F. Gobet, F. Hannachi, M. Tarisien, M. Versteegen, M. M. Aléonard. Rev. Sci. Instrum., 84, 103510(2013).
Get Citation
Copy Citation Text
Siyu Chen, Wenchao Yan, Mingyang Zhu, Yaojun Li, Xichen Hu, Hao Xu, Weijun Zhou, Guangwei Lu, Mingxuan Wei, Lin Lu, Xulei Ge, Boyuan Li, Xiaohui Yuan, Feng Liu, Min Chen, Liming Chen, Jie Zhang. A platform for all-optical Thomson/Compton scattering with versatile parameters[J]. High Power Laser Science and Engineering, 2025, 13(4): 04000e56
Category: Research Articles
Received: Mar. 14, 2025
Accepted: Apr. 16, 2025
Posted: Apr. 18, 2025
Published Online: Sep. 2, 2025
The Author Email:
CSTR:32185.14.hpl.2025.36







 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence

