The 2023 Nobel Prize in Physics awarded to Pierre Agostini, Ferenc Krausz and Anne L’Huillier ‘for experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter’[1] and the 2018 National Academies of Science report[2] that spurred the ‘Brightest Light Initiative’[3] highlight the impactful science enabled by producing the shortest possible pulses of light[4–6]. Recent advances in high-energy few-cycle pulse generation techniques[7,8] allow us to probe new physical effects, including those from the carrier-envelope phase[9–11], and to generate high laser intensities with moderate laser energies for applications such as relativistic plasma-based attosecond pulse generation[12]. These developments motivate the design of optical components with higher laser-induced damage thresholds (LIDTs) for few- to single-cycle pulses. The scaling of LIDTs with laser fluence is generally well understood for the tens of picosecond to nanosecond regimes[13], but is more complex for shorter pulses[14], especially few-cycle pulses[15,16].
High Power Laser Science and Engineering, Volume. 13, Issue 4, 04000e60(2025)
A fully three-dimensional kinetic particle-in-cell framework for modeling laser–dielectric interactions: few-cycle pulse damage
We present a fully three-dimensional kinetic framework for modeling intense short pulse lasers interacting with dielectric materials. Our work modifies the open-source particle-in-cell code EPOCH to include new models for photoionization and dielectric optical response. We use this framework to model the laser-induced damage of dielectric materials by few-cycle laser pulses. The framework is benchmarked against experimental results for bulk silica targets and then applied to model multi-layer dielectric mirrors with a sequence of simulations with varying laser fluence. This allows us to better understand the laser damage process by providing new insight into energy absorption, excited particle dynamics and nonthermal excited particle distributions. We compare common damage threshold metrics based on the energy density and excited electron density.
1 Introduction
Previous experimental work has explored the damage and ablation of
Understanding few-cycle pulse material interactions requires advances in computational and theoretical models. There has been significant work using one-dimensional finite-difference-time-domain (FDTD) simulations to model these interactions[26], with recent efforts in two dimensions[27,28]. FDTD simulations provide insight into the laser material interactions and can predict LIDTs, but do not capture the nonthermal nature of excited electrons, nor do they capture their ballistic motion. To expand our understanding of the interaction dynamics, we use particle-in-cell (PIC) simulations[29,30]. As with FDTD simulations, PIC codes solve Maxwell’s equations on a computational grid. In addition, PIC simulations statistically represent the neutral and excited particles in the simulation with a finite number of ‘macroparticles’[29–31]. The charged particles are then advanced using the Lorentz force and additional physical effects, including ionization and collisions, are often added.
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
PIC simulations are commonly used to study laser–plasma interactions (e.g., by Ziegler et al.[32]) and are increasingly being modified to simulate laser damage and related regimes. For example, Mitchell et al.[33] modeled crater formation in metals due to femtosecond laser ablation, Cochran et al.[34] modeled liquid-crystal plasma mirrors[35], Déziel et al.[36] studied laser-induced periodic surface structures and Ding et al.[37] and Do et al.[38] modeled plasmons using PIC simulations. Interactions of lasers with nano/micro-scale structures in silicon and
In this work, we begin in Section 2 by introducing the modifications and extensions we have made to a PIC code to model laser–dielectric interactions. Then in Section 3 we discuss the material properties and simulation setup for both bulk and multi-layer targets. Next, in Section 4 we compare the predictions of this framework to existing experimental results and discuss expected damage threshold metrics. Then we apply the framework to the modeling of multi-layer mirrors in Section 5 and conclude in Section 6.
2 Particle-in-cell simulation modifications
Our work extends the three-dimensional (3D) implementation of version 4.17.10 of the EPOCH[31] PIC code, which is designed for the study of high-energy-density physics. EPOCH is a popular open-source PIC code that can scale to run on thousands of central processing unit (CPU) cores, although we note that there are a variety of other open-source and proprietary PIC codes available with different features and implementations[44], such as graphics processing unit (GPU) operation (e.g., PIConGPU[45] and WarpX[46]). PIC simulations of laser–matter interactions are typically used to study only tens-to-hundreds of femtosecond timescales due to numerical instability issues and computational cost. As such, we focus on the initial laser–matter interaction and the resulting excited electron dynamics. For long-term dynamics and equilibration, one could use a final simulation state from a PIC model as the initial conditions for another model. For example, one could use the electron and ion temperatures in a two-temperature model, or consider tabulated equation of state values[16].
EPOCH includes multiple physics modules, but was not designed with laser–dielectric interactions in mind. Towards this goal, we have added a new photoionization model relevant for dielectric materials and a model for optical material properties, as discussed in the next sections.
2.1 Keldysh photoionization
Our work extends the existing ionization framework already available in EPOCH[31] to include the photoionization model developed by Keldysh[42]. The Keldysh ionization model allows us to calculate probabilities for electron transitions from the valence to the conduction band in solids due to the electric field of a laser pulse[47].
For a laser pulse with electric field amplitude
The Keldysh model is used in our simulations to calculate the probability that a given neutral macroparticle will ionize. When ionization occurs, a new electron macroparticle and corresponding ion macroparticle are created in place of the original macroparticle. Now we introduce the ionization rate equation used in our work. For brevity in the following expressions, we follow Refs. [48,49] by introducing the variables
We may then write the ionization rate
We note that this is the corrected version of the formulation, where the original contains a misprint as noted by Gruzdev[43]. Using the uncorrected version can result in significantly different calculations[28,43].
For our simulation framework, the Keldysh ionization rate is evaluated in situ (with the exception of the elliptic integrals, which are read from tabulated data files with 1000 points) rather than interpolated from a tabulated form, which facilitates accuracy over a wide range of fluences. We use the first 500 terms in this infinite sum in Equation (3), which is sufficient for the regimes of interest in this paper, as illustrated in the appendix, while limiting the computational cost. An adaptive approach to a prescribed tolerance could be employed in the future. Currently each macroparticle can only be ionized once.
While the Keldysh parameter depends on the laser amplitude
2.2 Collisional effects
We use the Pérez/Nanbu[51,52] binary collision module already included in the EPOCH code to account for collisions. The collision frequency in EPOCH is calculated for a charged particle
EPOCH includes a collisional ionization routine designed for atoms[31,54], but this is not well suited for impact ionization in dielectrics. A more appropriate ionization rate for our regime can be calculated with the approach by Keldysh[55], although some of the input parameters to the models are not well reported and may require fitting of output results to experimental data[41,56]. Impact ionization is reduced for shorter few-cycle pulses. Models by Petrov and Davis[57] suggest collisional ionization dominates photoionization for fluences exceeding
2.3 Refraction
The optical properties of dielectrics are modeled using a spatially varying permittivity
3 Simulation setup
We begin by applying this simulation framework to a slab of fused silica (
![]()
Figure 1.A schematic of the 3D simulations for bulk fused silica (a), and the coating of the multi-layer quarter-wave mirror with a fused 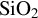 protective layer (b). The normally incident few-cycle laser pulse (c) is driven from the minimum y boundary into a 0.1 μm vacuum region before the target. The
protective layer (b). The normally incident few-cycle laser pulse (c) is driven from the minimum y boundary into a 0.1 μm vacuum region before the target. The 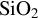 regions are represented in yellow and the
regions are represented in yellow and the 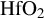 in blue. A cross-section of the multi-layer mirror in the
in blue. A cross-section of the multi-layer mirror in the  plane is shown in (d) (the
plane is shown in (d) (the  dimension is not to scale). The thickness of the top
dimension is not to scale). The thickness of the top 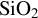 layer is 270.90 nm and then there are alternating layers of
layer is 270.90 nm and then there are alternating layers of 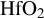 (98.95 nm) and
(98.95 nm) and 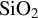 (135.45 nm).
(135.45 nm).
3.1 Grid and particle initialization
The simulation setup for bulk
Then we apply this framework to multi-layer interference coatings composed of alternating fused
Both series of simulations are initialized with 1000 neutral
3.2 Material properties

Table 1. Material properties used in simulations.
Table 1. Material properties used in simulations.
Band Index Density Material gap (eV) n (g cm−3) ${m}_\mathrm{h}^{\ast }$ ${m}_\mathrm{e}^{\ast }$ SiO2 9[ 26 ]1.477 2.2[ 62 ]8[ 63 ]0.6[ 63 ]HfO2 5.7[ 64 ]2.021 9.68 1.12[ 64 ]1.09[ 64 ]
4 Damage modeling of the bulk silica target
We benchmark our framework against the experiment by Chimier et al.[16,21], which finds damage with a fluence of
4.1 Electron density
For simulation and theoretical work, the predicted excited electron density is often used as a criterion to predict damage. Many studies use the critical electron density[69] for free electrons or some fraction of total ionization[70]. This qualitatively makes sense, as exceeding such thresholds can result in high absorption and subsequent damage. This choice has shown good agreement with longer pulses, although recent work has suggested that this description is insufficient for modeling shorter few-cycle pulses[16,71]. As shown in Figure 2, the damage threshold is predicted at about
![]()
Figure 2.The electron density at the center of the x–z plane (averaged over six cells in x and y) along y at 20 fs for a series of PIC simulations at various laser fluences with a 7 fs duration pulse interacting with bulk 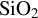 . The critical plasma density
. The critical plasma density 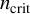 and electron instability density from Ref. [72] are labeled with dashed lines. The latter predicts damage around
and electron instability density from Ref. [72] are labeled with dashed lines. The latter predicts damage around 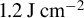 .
.
Alternatively, the instability density suggested by Stampfli and Bennemann[72] states that when the conduction band electron density reaches about 9% of the valence band electron density, the elastic shear constant will become negative and the lattice becomes unstable, which then leads directly to a very rapid melting of the crystal structure. This criterion was developed for crystals, but the fundamental physical principles – namely, the relationship between conduction band electron density and the stability of the atomic structure – are similar. By applying this criterion to the bulk fused
4.2 Energy density
The excited electron energy density criterion has also been suggested to predict damage[71,73]. The predicted energy density is typically compared to material properties, such as the dissociation energy, or an energy barrier associated with melting or boiling[71,74]. We compare the energy densities in our simulations to these thresholds.
Previous computational approaches typically assume some simple electron energy distribution, whereas in PIC simulation, the energy density can be calculated directly with standard outputs. For our simulations, we multiply the number density by average particle energy for a species in each cell. Alternately, this could be re-sampled to a finer or a coarser grid if the individual macroparticle positions and energies are extracted from the simulation.
Due to variations of reported material properties in the literature and uncertainty of previous simulations, the exact energy density for damage is not agreed upon. For reference, the dissociation energy of
The energy densities related to melting or boiling are lower, where we can use the temperature-dependent heat capacity and latent heat of vaporization used by Zhao et al.[78,79] to calculate an energy density of
Figure 3 shows the maximum energy density in simulations with and without collisions for a range of laser fluences. The simulations just including photoionization, (without collisions) have lower energy density at the end of the simulation and do not exceed the boiling criterion until much higher fluences are expected for the LIDT in these conditions.
![]()
Figure 3.The peak energy density for the series of PIC simulations at various fluences with a 7 fs duration pulse interacting with bulk fused silica. The experiment[16] being modeled observed damage around 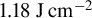 and ablation[21] at
and ablation[21] at 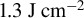 . The shaded horizontal line/bands indicate approximate energy density thresholds for melting, boiling and dissociation. The shaded vertical bands represent uncertainty in experimental damage and ablation thresholds. The simulations including collisions have a higher predicted energy density. Including both our Keldysh photoionization model and collisional effects shows agreement between the expected damage fluence and the dissociation energy.
. The shaded horizontal line/bands indicate approximate energy density thresholds for melting, boiling and dissociation. The shaded vertical bands represent uncertainty in experimental damage and ablation thresholds. The simulations including collisions have a higher predicted energy density. Including both our Keldysh photoionization model and collisional effects shows agreement between the expected damage fluence and the dissociation energy.
In Figure 3, we see that at
4.3 Kinetic particle motion
The kinetic nature of PIC simulations allows us to explore the energy and motion of the excited electrons. While most previous approaches assume a thermal distribution of the excited electrons, Figure 4 shows that this is not the case during the interaction. The spectra at different times of the simulation are shown and the energy is fitted by the
![]()
Figure 4.Excited electron energy distributions in a 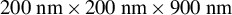 region of the target at the center of the interaction for a
region of the target at the center of the interaction for a 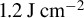 pulse. A simulation with just field ionization is shown in (a) and a simulation with field ionization and collisions is shown in (b). A fit with the given temperature is shown. We observe the nonthermal nature, especially for early times and for simulations without collisions.
pulse. A simulation with just field ionization is shown in (a) and a simulation with field ionization and collisions is shown in (b). A fit with the given temperature is shown. We observe the nonthermal nature, especially for early times and for simulations without collisions.
5 Damage modeling of multi-layer mirrors
For the multi-layer dielectric mirror,
5.1 Electron density
As mentioned in Section 4, the plasma critical density may underestimate the damage threshold; it predicts the LIDT slightly above
![]()
Figure 5.The electron density at the center of the x–z plane along y at 20 fs for a series of PIC simulations at various fluences with a 7 fs duration pulse interacting with a multi-layer mirror. The yellow area is 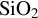 and blue area is
and blue area is 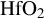 . Different critical electron densities are labeled in the figure with dashed lines.
. Different critical electron densities are labeled in the figure with dashed lines.
5.2 Energy density
The peak electron energy density along y at the center of the x–z plane in each layer with different fluences is shown in Figure 6. The dissociation energy of fused
![]()
Figure 6.The peak electron energy density at the center of the x–z plane along y at 20 fs for a series of PIC simulations at various fluences with a 7 fs duration pulse interacting with a multi-layer mirror. The yellow area is fused 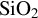 and blue area is fused
and blue area is fused 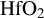 . The
. The 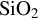 boiling and melting energy densities are at about
boiling and melting energy densities are at about 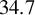 and
and 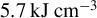 , respectively, indicated as yellow dashed lines, and the
, respectively, indicated as yellow dashed lines, and the 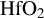 boiling and melting energy densities are at about
boiling and melting energy densities are at about 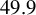 and
and 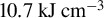 , respectively, indicated as blue dashed lines.
, respectively, indicated as blue dashed lines.
Instead let us consider energy density thresholds for melting and boiling, as these may relate to damage within the layers of a coating. To calculate the melting and boiling energy densities, we make the following assumptions: (i) the vaporization latent heat for
The boiling energy density criterion predicts the LIDT at a fluence between
5.3 Plasma screening effects
As shown in Figure 6, the global maximum energy density at low fluences is in the first
As the fluence increases beyond
To illustrate this process clearly, a two-dimensional y–z cross-section of the layers at the center of the x-axis is shown in Figure 7 at fluence of
![]()
Figure 7.The (a) energy density and (b) electron density at the center of x on the y–z plane at 20 fs and 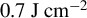 with a 7 fs duration pulse interacting with a multi-layer mirror. The mirror surface starts at y = 0, and the dashed red lines are the interfaces between layers. The white areas have no excited electrons. (c) The maximum accumulated normalized intensity over the entire simulation.
with a 7 fs duration pulse interacting with a multi-layer mirror. The mirror surface starts at y = 0, and the dashed red lines are the interfaces between layers. The white areas have no excited electrons. (c) The maximum accumulated normalized intensity over the entire simulation.
Noticeably, the electron density, energy density and intensity profiles in the protective
Furthermore, in Figure 6, the first
The plasma generation could also imply the breakdown threshold, which is defined as a permanent change to the optical properties. We can see from both the energy and electron density profiles that the local peak in the top
5.4 Particle energy
The kinetic nature of the excited electrons is shown in Figure 8. The spectrum of the electrons in the
![]()
Figure 8.The energy histogram for the electrons in the first 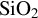 layer (a) and
layer (a) and 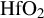 layer (b) at 6, 10, 24 fs for the
layer (b) at 6, 10, 24 fs for the 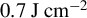 simulation with
simulation with 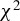 distribution fitted. The black curve is the Maxwell–Boltzmann distribution given the average energy at the stable stage around 24 fs.
distribution fitted. The black curve is the Maxwell–Boltzmann distribution given the average energy at the stable stage around 24 fs.
5.5 Particle dynamics
The peak intensity of the
In gases, electrons with kinetic energies exceeding
![]()
Figure 9.The 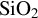 and
and 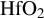 electron energy spatial distribution for a fluence of
electron energy spatial distribution for a fluence of 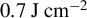 is shown on the left-hand side at 24 fs. The highest energy particles are found in the center of the first layer and at the interfaces between layers. Particle trajectories for random 2% of electrons with low (below average) final energy demonstrate the ionization dynamics in the first
is shown on the left-hand side at 24 fs. The highest energy particles are found in the center of the first layer and at the interfaces between layers. Particle trajectories for random 2% of electrons with low (below average) final energy demonstrate the ionization dynamics in the first 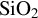 layer up to 16 fs (after the pulse has left). Ionization near the surface generally occurs at later times, as indicated by the color of the tracks.
layer up to 16 fs (after the pulse has left). Ionization near the surface generally occurs at later times, as indicated by the color of the tracks.
The tracks of select electrons in the first
6 Conclusion
Understanding few-cycle pulse interactions with dielectric optical components and their LIDT is essential for advancing next-generation laser systems. The use of kinetic simulations in relevant regimes is becoming increasingly popular[33,36,37,41]. Kinetic simulations allow us to capture the nonthermal nature of the initial interaction, which is important to accurately model absorption and ionization. We show that both excited electron density and energy density provide insight into the LIDT. Our framework shows good agreement with experimental LIDTs for bulk silica targets. Multi-layer mirror simulations indicate that plasma screening effects can alter the laser interaction and electron energy distribution for high fluences.
In the future, this framework can be applied to a variety of mirror and grating designs[28] for both near- and mid-infrared wavelengths[39,99]. In addition, simulations can be inserted into an optimization algorithm to optimize the LIDT or other properties of interest for optical components[100]. This framework already provides a deeper qualitative understanding of the dynamics of laser damage, and we show promising quantitative agreement with experiments for few-cycle pulses. Further development of this framework, including impact ionization[41,54], coupled with more precise measurements of material properties for relevant optical coating designs, can allow further validation of the framework across large ranges of laser fluence.
Appendix A: Keldysh ionization model implementation
Here we include additional implementation details for our Keldysh ionization model in EPOCH. As stated in Section 2.1, we use 500 terms in the infinite sum in
![]()
Figure 10.Percent error for 10–500 terms in the infinite sum in 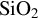 at varying laser intensities. The error is calculated with the result for 1000 terms as the ‘actual’ value. Our simulation framework uses 500 terms, which shows a negligible difference compared to 1000 terms for these intensities. The errors for
at varying laser intensities. The error is calculated with the result for 1000 terms as the ‘actual’ value. Our simulation framework uses 500 terms, which shows a negligible difference compared to 1000 terms for these intensities. The errors for 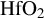 (not shown) are of similar magnitude to those for
(not shown) are of similar magnitude to those for 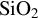 .
.
The Dawson integral (
[2] . Opportunities in Intense Ultrafast Lasers: Reaching for the Brightest Light(2018).
[4] M. Ferray, A. L’Huillier, X. F. Li, L. A. Lompre, G. Mainfray, C. Manus. J. Phys. B, 21, L31(1988).
[5] P.-M. Paul, E. S. Toma, P. Breger, G. Mullozt, F. Augé, P. Balcou, H. G. Muller, P. Agostini. Science, 292, 1689(2001).
[6] M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher, F. Krausz. Nature, 414, 509(2001).
[7] T. Brabec, F. Krausz. Rev. Mod. Phys., 72, 545(2000).
[8] T. Nagy, P. Simon, L. Veisz. Adv. Phys. X, 6, 1845795(2021).
[9] T. Wittmann, B. Horvath, W. Helml, M. G. Schätzel, X. Gu, A. L. Cavalieri, G. G. Paulus, R. Kienberger. Nat. Phys., 5, 357(2009).
[10] F. Mackenroth, A. Di Piazza, C. H. Keitel. Phys. Rev. Lett., 105, 063903(2010).
[11] J. Huijts, I. A. Andriyash, L. Rovige, A. Vernier, J. Faure. Phys. Plasmas, 28, 043101(2021).
[12] A. Cavagna, M. Eder, E. Chowdhury, A. Kalouguine, J. Kaur, G. Mourou, S. Haessler, R. Lopez-Martens. Opt. Lett., 50, 165(2025).
[13] B. C. Stuart, M. D. Feit, S. Herman, A. M. Rubenchik, B. W. Shore, M. D. Perry. J. Opt. Soc. Am. B, 13, 459(1996).
[14] D. Du, X. Liu, G. Korn, J. Squier, G. Mourou. Appl. Phys. Lett., 64, 3071(1994).
[15] M. Lenzner, J. Krüger, S. Sartania, Z. Cheng, Ch. Spielmann, G. M., W. Kautek, F. Krausz. Phys. Rev. Lett., 80, 4076(1998).
[16] B. Chimier, O. Utéza, N. Sanner, M. Sentis, T. Itina, P. Lassonde, F. Légaré, F. Vidal, J. C. Kieffer. Phys. Rev. B, 84, 094104(2011).
[17] M. Lenzner, J. Krüger, W. Kautek, F. Krausz. Appl. Phys. A, 68, 369(1999).
[18] K. R. P. Kafka, N. Talisa, G. Tempea, D. R. Austin, C. Neacsu, E. A. Chowdhury. Opt. Express, 24, 28858(2016).
[19] N. Sanner, O. Utéza, B. Chimier, M. Sentis, P. Lassonde, F. Légaré, J. C. Kieffer. Appl. Phys. Lett., 96, 071111(2010).
[20] L. Hoffart, P. Lassonde, F. Légaré, F. Vidal, N. Sanner, O. Utéza, M. Sentis, J.-C. Kieffer, I. Brunette. Opt. Express, 19, 230(2011).
[21] O. Utéza, N. Sanner, B. Chimier, A. Brocas, N. Varkentina, M. Sentis, P. Lassonde, F. Légaré, J. C. Kieffer. Appl. Phys. A, 105, 131(2011).
[22] N. Talisa, A. Alshafey, M. Tripepi, J. Krebs, A. Davenport, E. Randel, C. S. Menoni, E. A. Chowdhury. Opt. Lett., 45, 2672(2020).
[23] M. Kowalczyk, N. Nagl, P. Steinleitner, N. Karpowicz, V. Pervak, A. Głuszek, A. Hudzikowski, F. Krausz, K. F. Mak, A. Weigel. Optica, 10, 801(2023).
[24] D. Hui, H. Alqattan, S. Zhang, V. Pervak, E. Chowdhury, M. Th. Hassan. Sci. Adv., 9, eadf1015(2023).
[25] L. Argenti, M. Chini, L. Fang. Proceedings of the 8th International Conference on Attosecond Science and Technology(2024).
[26] J. R. Peñano, P. Sprangle, B. Hafizi, W. Manheimer, A. Zigler. Phys. Rev. E, 72, 036412(2005).
[27] S. Zhang, A. Davenport, N. Talisa, J. R. Smith, C. S. Menoni, V. E. Gruzdev, E. A. Chowdhury. Proc. SPIE, 11514, 115141T(2020).
[28] S. Zhang, C. Menoni, V. Gruzdev, E. Chowdhury. Nanomaterials, 12, 1259(2022).
[29] C. K. Birdsall, A. B. Langdon. Plasma Physics via Computer Simulation(2004).
[30] R. Hockney, J. Eastwood. Computer Simulations Using Particles(1988).
[31] T. D. Arber, K. Bennett, C. S. Brady, A. Lawrence-Douglas, M. G. Ramsay, N. J. Sircombe, P. Gillies, R. G. Evans, H. Schmitz, A. R. Bell, C. P. Ridgers. Plasma Phys. Control. Fusion, 57, 113001(2015).
[32] T. Ziegler, I. Göthel, S. Assenbaum, C. Bernert, F.-E. Brack, T. E. Cowan, N. P. Dover, L. Gaus, T. Kluge, S. Kraft, F. Kroll, J. Metzkes-Ng, M. Nishiuchi, I. Prencipe, T. Püschel, M. Rehwald, M. Reimold, H.-P. Schlenvoigt, M. E. P. Umlandt, M. Vescovi, U. Schramm, K. Zeil. Nat. Phys., 20, 1211(2024).
[33] R. A. Mitchell, D. W. Schumacher, E. A. Chowdhury. Opt. Lett., 40, 2189(2015).
[34] G. E. Cochran, P. L. Poole, D. W. Schumacher. Phys. Plasmas, 26, 103103(2019).
[35] P. B. Corkum. Phys. Rev. Lett., 71, 1994(1993).
[36] J.-L. Déziel, L. J. Dubé, S. H. Messaddeq, Y. Messaddeq, C. Varin. Phys. Rev. B, 97, 205116(2018).
[37] W. J. Ding, J. Z. J. Lim, H. T. B. Do, X. Xiong, Z. Mahfoud, C. E. Png, M. Bosman, L. K. Ang, L. Wu. Nanophotonics, 9, 3303(2020).
[38] H. T. B. Do, D. W. Jun, Z. Mahfoud, W. Lin, M. Bosman. Nanoscale, 13, 2801(2021).
[39] M. R Shcherbakov, G. Sartorello, S. Zhang, J. Bocanegra, M. Bosch, M. Tripepi, N. Talisa, A. AlShafey, J. Smith, S. Londo, F. Légaré, E. Chowdhury, G. Shvets. Nat. Commun., 14, 6688(2023).
[40] J. R Smith, S. Zhang, V. E Gruzdev, E. A Chowdhury. Conference on Lasers and Electro-Optics (CLEO), 1(2021).
[41] P.-J. Charpin, K. Ardaneh, B. Morel, R. Giust, F. Courvoisier. Opt. Express, 32, 10175(2024).
[42] L. V. Keldysh. JETP, 20, 1307(1965).
[43] V. E. Gruzdev. Proc. SPIE, 5506, 138(2004).
[44] J. R. Smith, C. Orban, N. Rahman, B. McHugh, R. Oropeza, E. A. Chowdhury. Phys. Plasmas, 28, 074505(2021).
[45] H. Burau, R. Widera, W. Hönig, G. Juckeland, A. Debus, T. Kluge, U. Schramm, T. E. Cowan, R. Sauerbrey, M. Bussmann. IEEE Trans. Plasma Sci., 38, 2831(2010).
[46] L. Fedeli, A. Huebl, F. Boillod-Cerneux, T. Clark, K. Gott, C. Hillairet, S. Jaure, A. Leblanc, R. Lehe, A. Myers, C. Piechurski, M. Sato, N. Zaim, W. Zhang, J.-L. Vay, H. Vincenti. SC22: International Conference for High Performance Computing, Networking, Storage and Analysis, 1(2022).
[47] V. E. Gruzdev. Proc. SPIE, 5647, 480(2005).
[48] A.-C. Tien, S. Backus, H. Kapteyn, M. Murnane, G. Mourou. Phys. Rev. Lett., 82, 3883(1999).
[49] P. Balling, J. Schou, Rep. Prog. Phys., 76, 036502(2013).
[50] D. Terzani, P. Londrillo. Comput. Phys. Commun., 242, 49(2019).
[51] F. Pérez, L. Gremillet, A. Decoster, M. Drouin, E. Lefebvre. Phys. Plasmas, 19, 083104(2012).
[52] K. Nanbu, S. Yonemura. J. Comput. Phys., 145, 639(1998).
[53] Y. T. Lee, R. M. More. Phys. Fluids, 27, 1273(1984).
[54] S. Morris, T. Goffrey, K. Bennett, T. Arber. Phys. Plasmas, 29, 123907(2022).
[55] L. V. Keldysh. JETP, 21, 1135(1965).
[56] J.-L. Déziel, L. J. Dubé, C. Varin. Phys. Rev. B, 104, 045201(2021).
[57] G. M. Petrov, J. Davis. J. Phys. B, 41, 025601(2008).
[58] B. Rethfeld. Phys. Rev. B, 73, 035101(2006).
[59] C. Varin, R. Emms, G. Bart, T. Fennel, T. Brabec. Comput. Phys. Commun., 222, 70(2018).
[60] R. Courant, K. Friedrichs, H. Lewy. Math. Ann., 100, 32(1928).
[61] R. Courant, K. Friedrichs, H. Lewy. IBM J. Res. Develop., 11, 215(1967).
[62] W. M. Haynes. CRC Handbook of Chemistry and Physics(2012).
[63] V. A. Gritsenko, R. M. Ivanov, Y. N. Morokov. J. Exp. Theor. Phys., 81, 1208(1995).
[64] T. V. Perevalov, V. A. Gritsenko, S. B. Erenburg, A. M. Badalyan, H. Wong, C. W. Kim. J. Appl. Phys., 101, 053704(2007).
[65] V. Gruzdev. Proc. SPIE, 7842, 784216(2010).
[66] S. Zhang, M. Tripepi, A. AlShafey, N. Talisa, H. T. Nguyen, B. A. Reagan, E. Sistrunk, D. J. Gibson, D. A. Alessi, E. A. Chowdhury. Opt. Express, 29, 39983(2021).
[67] C. N. Danson, C. Haefner, J. Bromage, T. Butcher, J.-C. F. Chanteloup, E. A. Chowdhury, A. Galvanauskas, L. A. Gizzi, J. Hein, D. I. Hillier, N. W. Hopps, Y. Kato, E. A. Khazanov, R. Kodama, G. Korn, R. Li, Y. Li, J. Limpert, J. Ma, C. H. Nam, D. Neely, D. Papadopoulos, R. R. Penman, L. Qian, J. J. Rocca, A. A. Shaykin, C. W. Siders, C. Spindloe, S. Szatmári, R. M. G. M. Trines, J. Zhu, P. Zhu, J. D. Zuegel. High Power Laser Sci. Eng., 7, e54(2019).
[68] P. L. Poole, C. Willis, R. L. Daskalova, K. M. George, S. Feister, S. Jiang, J. Snyder, J. Marketon, D. W. Schumacher, K. U. Akli, L. Van Woerkom, R. R. Freeman, E. A. Chowdhury. Appl. Opt., 55, 4713(2016).
[69] F. F. Chen. Introduction to Plasma Physics and Controlled Fusion(2016).
[70] K. Werner, V. Gruzdev, N. Talisa, K. Kafka, D. Austin, C. M Liebig, E. Chowdhury. Sci. Rep., 9, 19993(2019).
[71] P. A. Zhokhov, A. M. Zheltikov. Sci. Rep., 8, 1824(2018).
[72] P. Stampfli, K. H. Bennemann. Phys. Rev. B, 42, 7163(1990).
[73] M. Grehn, T. Seuthe, M. Höfner, N. Griga, C. Theiss, A. Mermillod-Blondin, M. Eberstein, H. Eichler, J. Bonse. Opt. Mater. Express, 4, 689(2014).
[74] H. Wang, H. Qi, J. Zhao, B. Wang, J. Shao. Opt. Commun., 387, 214(2017).
[75] T. Q. Jia, Z. Z. Xu, R. X. Li, D. H. Feng, X. X. Li, C. F. Cheng, H. Y. Sun, N. S. Xu, H. Z. Wang. J. Appl. Phys., 95, 5166(2004).
[76] S. Inaba, S. Fujino, K. Morinaga. J. Am. Ceramic Soc., 82, 3501(1999).
[77] R. P. Drake. High-Energy-Density Physics(2006).
[78] J. Zhao, J. Sullivan, J. Zayac, T. D. Bennett. J. Appl. Phys., 95, 5475(2004).
[79] L. Zhao, J. Cheng, M. Chen, X. Yuan, W. Liao, H. Wang, Q. Liu, H. Yang. Results Phys., 12, 1363(2019).
[80] D. Bäuerle. Laser Processing and Chemistry(2013).
[81] R. G. Kraus, S. T. Stewart, D. C. Swift, C. A. Bolme, R. F. Smith, S. Hamel, B. D. Hammel, D. K. Spaulding, D. G. Hicks, J. H. Eggert, G. W. Collins. J. Geophys. Res. Planets, 117, E9(2012).
[82] R. S. Khmyrov, S. N. Grigoriev, A. A. Okunkova, A. V. Gusarov. Phys. Procedia, 56, 345(2014).
[83] I. S. Grigoriev, E. Z. Meilikhov. Handbook of Physical Quantities(1997).
[84] G. V. Samsonov. The Oxide Handbook(2013).
[85] P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, l. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt. Nat. Methods, 17, 261(2020).
[86] M. Mero, J. Liu, W. Rudolph, D. Ristau, K. Starke. Phys. Rev. B, 71, 115109(2005).
[87] H. Wang, H. Qi, J. Zhao, B. Wang, J. Shao. Opt. Commun., 387, 214(2017).
[88] C. Wang, M. Zinkevich, F. Aldinger. J. Am. Ceramic Soc., 89, 3751(2006).
[89] W. A. Roth, G. Becker. Z. Phys. Chem., 159A, 1(1932).
[90] G. L. Humphrey. J. Am. Chem. Soc., 75, 2806(1953).
[91] E. J. Huber, C. E. Holley. J. Chem. Eng. Data, 13, 252(1968).
[92] A. N. Kornilov, I. M. Ushakova, E. J. Huber, C. E. Holley. J. Chem. Thermodyn., 7, 21(1975).
[93] Y. N. Paputskii, V. A. Krzhizhanovaskaya, V. B. Glushkova. Inorg. Mater, 10, 1338(1974).
[94] M. B. Panish, L. Reif. J. Chem. Phys., 38, 253(1963).
[95] J. J. Low, N. H. Paulson, M. D’Mello, M. Stan. Calphad, 72, 11(2020).
[96] G. Geoffroy, G. Duchateau, N. Fedorov, P. Martin, S. Guizard. Laser Phys., 24, 086101(2014).
[97] G. G. Paulus, W. Becker, W. Nicklich, H. Walther. J. Phys. B, 27, L703(1994).
[98] G. Duchateau, G. Geoffroy, A. Dyan, H. Piombini, S. Guizard. Phys. Rev. B, 83, 075114(2011).
[99] D. R. Austin, K. R. P. Kafka, Y. H. Lai, Z. Wang, C. I. Blaga, E. A. Chowdhury. Opt. Lett., 43, 3702(2018).
[100] J. R. Smith, C. Orban, J. T. Morrison, K. M. George, G. K. Ngirmang, E. A. Chowdhury, W. M. Roquemore. New J. Phys., 22, 103067(2020).
[102] W. J. Cody, K. A. Paciorek, H. C. Thacher. Math. Comput., 24, 171(1970).
[104] J. D. Hunter. Comput. Sci. Eng., 9, 90(2007).
[105] C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke, T. E. Oliphant. Nature, 585, 357(2020).
Get Citation
Copy Citation Text
Joseph R. Smith, Ziyao Su, Simin Zhang, Charles Varin, Vitaly E. Gruzdev, Enam A. Chowdhury. A fully three-dimensional kinetic particle-in-cell framework for modeling laser–dielectric interactions: few-cycle pulse damage[J]. High Power Laser Science and Engineering, 2025, 13(4): 04000e60
Category: Research Articles
Received: Mar. 4, 2025
Accepted: Jun. 5, 2025
Published Online: Sep. 15, 2025
The Author Email:







 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence

