Real-time observation of picosecond-timescale optical quantum entanglement towards ultrafast quantum information processing

Feb. 20 , 2025SJ_Zhang

Abstract

Entanglement is a fundamental resource for various optical quantum information processing (QIP) applications. To achieve high-speed QIP systems, entanglement should be encoded in short wavepackets. Here we report the real-time observation of ultrafast optical Einstein–Podolsky–Rosen correlation at a picosecond timescale in a continuous-wave system. Optical phase-sensitive amplification using a 6-THz-bandwidth waveguide-based optical parametric amplifier enhances the effective efficiency of 70-GHz-bandwidth homodyne detectors, mainly used in 5G telecommunication, enabling its use in real-time quantum state measurement. Although power measurement using frequency scanning, such as an optical spectrum analyser, is not performed in real time, our observation is demonstrated through the real-time amplitude measurement and can be directly used in QIP applications. The observed Einstein–Podolsky–Rosen states show quantum correlation of 4.5 dB below the shot-noise level encoded in wavepackets with 40 ps period, equivalent to 25 GHz repetition—10³ times faster than previous entanglement observation in continuous-wave systems. The quantum correlation of 4.5 dB is already sufficient for several QIP applications, and our system can be readily extended to large-scale entanglement. Moreover, our scheme has high compatibility with optical communication technology such as wavelength-division multiplexing, and femtosecond-timescale observation is also feasible. Our demonstration is a paradigm shift in accelerating accessible quantum correlation—the foundational resource of all quantum applications—from the nanosecond to picosecond timescales, enabling ultrafast optical QIP.

Main

Quantum entanglement is a fundamental concept of quantum mechanics^1,2, as well as a basic resource for various applications of quantum information processing (QIP), such as quantum computation^3,4, quantum communication^5,6,7 and quantum cryptography^8,9,10. Since light has a carrier frequency of hundreds of terahertz and is compatible with the highly developed optical communication technology, it is attracting attention as a promising platform for realizing these QIP applications with high clock frequencies. In particular, the generation of large-scale quantum entangled states, called cluster states, has already been reported in continuous-variable (CV) optical systems^11,12. Cluster states are resources for large-scale measurement-based quantum computation (MBQC)^13,14 and quantum communication¹³, and such large-scale CV quantum entanglement is expected to be a basic technology towards optical QIP. One of the main directions in the development of CV optical quantum technology is to speed up the system clock frequency. Higher clock frequency can treat more information per unit time in a single optical channel, leading to more efficient QIP. Moreover, in the context of quantum communication such as quantum key distribution or quantum repeaters, a higher clock frequency could be useful in increasing the trial rate. As quantum states are defined in a temporal wavepacket in CV optical QIP, the time width of the wavepacket has to be reduced to accelerate the system clock. Note that the time width of a wavepacket determines the system lock only in continuous-wave systems, whereas the repetition rate does in the pulsed systems.

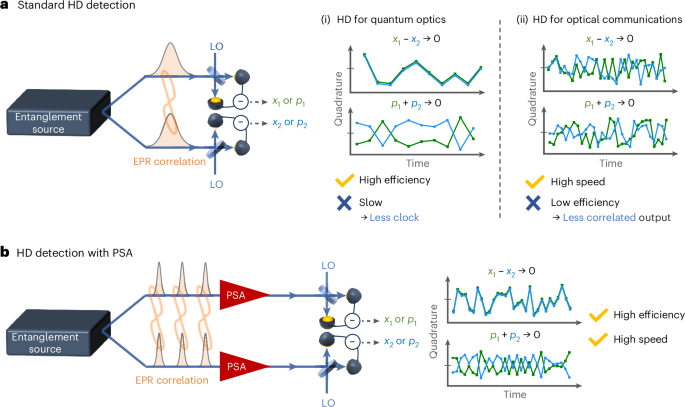
An example of the approach to shorten the wavepacket is the single-path waveguide optical parametric amplifier (OPA)^15,16,17. This OPA has terahertz bandwidth and, in principle, it can generate a squeezed light defined in sub-picosecond-timescale wavepacket, attracting attention as a next-generation ultrafast light source. By contrast, the usage of quantum entanglement, such as CV-MBQC or quantum communication, is based on the ‘measurement’ of a wavepacket and ‘feed-forward’ based on the measurement results. Therefore, in addition to ‘state preparation’ with short wavepackets, speeding up the measurement is also critical for CV optical QIP. In particular, as quantum information in CV-QIP is encoded in the phase space, the measurement of our interest is the real-time amplitude measurement. This measurement is the homodyne measurement¹⁸, which has been a basic optical technique for measuring the real-time amplitude, that is, the quadrature operators. Note that power measurement using frequency scanning, such as optical spectrum analysers with terahertz bandwidth, is not performed in real time and irrelevant to actual optical QIP applications. Figure 1a shows the trade-off between the speed and efficiency of the conventional homodyne measurement. To ensure that we extract correct quadrature values, the efficiency of the measurement must be high, and this limits the other specification of the photodiode. Experimentally, a high-efficiency (more than 95%) homodyne detector has been realized with a frequency bandwidth of up to 200 MHz (ref. ¹⁹). With recent developments in optical communication technologies for 5G or 6G communication systems, balanced detectors with bandwidths of up to 113 GHz are now available²⁰. These high-speed homodyne detectors, however, are developed for coherent lights that are robust to loss and the high-frequency bandwidth is achieved by trading efficiency (~50%) for bandwidth, making them incompatible with quantum measurement. This trade-off relationship has limited the system clock of the quantum state generation and operation^19,21 to the timescale of tens of nanoseconds at least. Although many technical challenges to overcome remain for QIP applications such as nonlinear feed-forward or non-Gaussian-state preparation, progress has been made in the development of both electro-optic and electrical devices, which are now on the path to operating at sub-nanosecond timescales^22,23, highlighting homodyne detection as the key limiting factor for the operational speed of optical QIP systems. Consequently, the speed of these systems remains much slower than that of classical optical communication systems, whose clock cycles are in the sub-nanosecond range, or gate operations in other physical quantum systems, which have achieved performance on the order of a few nanoseconds^24,25. To the best of our knowledge, the shortest record for optical entanglement observation involves 40 ns wavepackets¹¹.

**Fig. 1: Schematic of the measurement of EPR correlation using homodyne measurement.**

To overcome this trade-off limitation, a phase-sensitive amplifier (PSA)²⁶ has attracted attention recently as a tool for applying this low-efficiency and high-speed homodyne detector to quantum optics technologies. Figure 1b shows the schematic of this approach. Here the PSA acts on the quantum states before the homodyne measurement. The role of the PSA is to act as a preamplifier with 0 dB noise figure, in principle, enabling high-precision quantum measurements, even when the efficiency of the subsequent homodyne detectors is low. A PSA in an optical system can be emulated by parametric amplification and has been demonstrated experimentally^15,27,28. Most of these demonstrations, however, measure the quadrature ‘power’ and not their real-time amplitude, making them less relevant to actual QIP applications. A demonstration of measurement of real-time quadrature amplitude in this manner was done using a low-loss, high-gain OPA, and the real-time quadrature values of the squeezed light have been measured up to 43 GHz bandwidth²⁹. In all of these previous demonstrations, regardless of whether it is ‘power’ or ‘amplitude’ measurement, the preparation and measurement are limited to squeezed light defined in the single mode and never extended to quantum entanglement, that is, the multimode quantum state, which is the fundamental resources for all QIP applications.

Here, we demonstrate the generation and real-time measurement of ultrafast Einstein–Podolsky–Rosen (EPR) state, the most primitive CV quantum entangled state by using homodyne measurement with a PSA. We observe a quantum correlation of more than 4.5 dB below the shot-noise level encoded in a wavepacket with 40 ps period, equivalent to 25 GHz repetition—10³ times faster than conventional quantum entanglement observation. The observed EPR states have autocorrelation with 20 ps time width, meaning that we can introduce tens-of-picoseconds wavepacket to exploit their quantum correlation. To the best of our knowledge, the demonstration of EPR state generation using a waveguide OPA has never been done before, and the correlation level observed here is already sufficient for some applications in optical CV-QIP^11,30. For this experiment, we develop a new phase-locking method for homodyne measurements with a PSA on two-mode states. Our method is not limited to two-mode states, but can be readily extended to the multimode quantum states and large-scale quantum entangled state previously demonstrated^11,12. Moreover, our scheme has a high compatibility with optical communication technology; femtosecond-timescale observation is also feasible by using wavelength-division multiplexing. Our demonstration is a milestone towards ultrafast QIP applications via quantum entanglement.

Results

Homodyne detection using a PSA

Figure 2 shows the schematic of the experimental setup and the details are described in the Methods. The squeezed light sources and the PSAs in this experiment are periodically poled lithium niobate waveguide OPAs³¹ developed by our group. First, squeezed lights are generated in the two generation OPAs and they are interfered in such a relative phase that the directions of squeezing are orthogonal. This results in a two-mode squeezed state that approaches the EPR state in the infinite-squeezing limit. Formally, let us consider the correlation of the quadrature amplitudes, which will be denoted by ?^ and ?^ satisfying [?^,?^]=?. If we assume that the two squeezed lights have the same squeezing parameter r, then the quadrature amplitudes of the output modes after the interference satisfy ?^1−?^2=2e−??^vac,?^1+?^2=2e−??^vac, where the indices 1 and 2 are the mode indices and ?^vac and ?^vac represent the quadrature amplitudes of the vacuum states. At the infinite-squeezing limit, that is, r approaching infinity, the quadrature amplitudes ?^ (?^) will have perfect (anti)correlation³².

After the generation of the two-mode squeezed states, each mode enters the PSA at the measurement OPAs. The role of the measurement OPAs is to amplify the quadrature. This amplification acts only on a single phase of the quadrature, allowing amplification with 0 dB noise figure, in principle, which reduces the degradation of the EPR correlation due to the losses of the homodyne detectors. On the contrary, the quadrature amplitude that is orthogonal to the amplified phase will be compressed, making it more vulnerable to noise. This does not affect the final measurement if we are measuring quadrature amplitudes at the amplified phase. This scheme improves the speed and efficiency of homodyne measurements independent of the input state and can, therefore, be applied not only to EPR correlations but also to arbitrary quantum states. Note, however, that the relative phase between the amplified quadrature and the local oscillator light of the homodyne detector will be important as they determine the efficiency of the preamplification with the PSA in measuring the EPR correlation. The efficiency of the measurement system²⁹, which consists of the measurement OPAs and the high-speed homodyne detector, can be expressed as

?meas=?OPA?HD?HD+1−?HD?, (1)

and the total efficiency of the experimental setup is written by

?total=?state?meas. (2)

Here η_OPA, η_HD, η_state and G are the efficiency of the OPA used for the PSA, efficiency of homodyne detection, efficiency of state preparation and amplification gain of the PSA, respectively. From equation (1), we see that when there is no amplification (G = 1 (0 dB)), the measurement efficiency is η_OPAη_HD, whereas in the limit of large amplification gain, the measurement efficiency becomes η_OPA. Thus, the amplification suppresses the effect of the optical losses of the homodyne detector.

Raw data from real-time 110 GHz oscilloscope

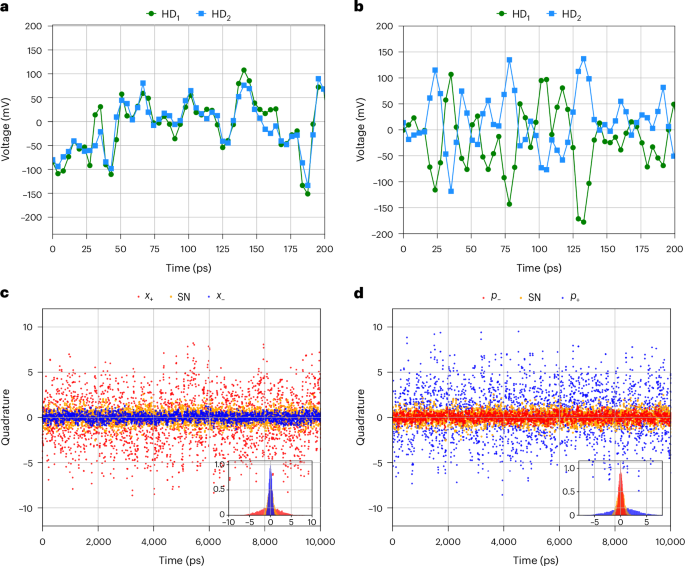
Figure 3 shows the real-time signal measured by the oscilloscope. The real-time signals clearly show correlation and anticorrelation in x and p quadrature amplitudes on the picosecond timescale, respectively. It is notable that this measurement is the real-time amplitude measurement and these outputs can be directly utilized in QIP operations. The timescale of the real-time signal is limited by the sampling rate (256 gigasamples per second) and the bandwidth (113 GHz) of the oscilloscope (Methods). In the ideal case, the quadratures would be perfectly correlated or anticorrelated and the imperfections observed here are due to factors such as finite squeezing and optical losses in the system. Quantitative evaluation and verification of quantum entanglement between these two modes can be done by calculating the noise power of the linear combinations of the quadrature amplitudes given by ?+=(?1+?2)/2,?−=(?1−?2)/2,?+=(?1+?2)/2 and ?−=(?1−?2)/2, and comparing them with the shot-noise level.

**Fig. 3: Real-time quantum correlation signal.**

Analysis on quantum correlation in time domain

Figure 4a,b shows the autocorrelation functions of x_± and p_±, respectively. Autocorrelation function ?cor±(?) is defined as ?cor±(?)=⟨?±(?)?±(?+?)⟩? and characterizes quantum correlation in the time domain. Here 〈…〉_t represents the temporal average over time t, indicating the expectation value with respect to t. From Fig. 4a,b, we can see that both x₋ and p₊ are below the shot-noise level at around τ = 0. The values at τ = 0 represent the noise power of the quadrature amplitudes shown in Fig. 3c,d, and x₋ and p₊ are both 4.0 dB below the shot-noise level at τ = 0, respectively. These levels of quantum correlations satisfy the inseparability criterion for CV entangled states^33,34,35, meaning that we have succeeded in the generation and measurement of quantum entanglement. Moreover, Fig. 4a,b shows that the time widths of autocorrelations are around 20 ps. When considering the use of entanglement in QIP applications, it is necessary for adjacent wavepackets to be independent and uncorrelated. Therefore, the width of the autocorrelation function sets a lower limit on the clock cycle of the QIP system. Both broadband squeezed light source and high-speed measurement enable this ultrafast quantum correlation observation at the timescale of tens of picoseconds. As an example, we calculate the quantum correlation defined in a wavepacket (Supplementary Information provides details on the quantum correlation analysis using a wavepacket). The shape of the wavepacket is known to be useful for quantum computation³⁶ and the same shape as the one used in conventional quantum entanglement observations¹¹. Here only the time width is shortened by a factor of 10³ from the conventional research of 40 ns (ref. ¹¹), which is the previous record of the shortest timescale observation of entanglement. The obtained quantum correlations of x₋ and p₊ are below the shot-noise level by 4.7 dB and 4.5 dB, respectively, indicating the successful observation of quantum correlation with a 10³ times higher-speed system than conventional research.

**Fig. 4: Analysis on quantum correlation in the time domain.**

Discussion

In this experiment, we experimentally demonstrate the real-time observation of high-speed EPR states with quantum correlations of more than 4.5 dB. The time width of the wavepacket we use is more than 10³ times faster than the previous quantum entangled state observation¹¹. The correlation level of 4.5 dB can already be used in some applications; it exceeds the 3 dB requirement for entanglement swapping with unit gain³⁰, and 3 dB (ref. ¹²) or 4.5 dB (ref. ¹¹) required for the verification of two-dimensional cluster states towards CV-MBQC.

Further development of this research has three directions: ‘larger scale’, ‘higher speed’ and ‘stronger correlation’. Large-scale entanglement is an important aspect in the context of MBQC and quantum communication. The synchronization scheme for PSA-based homodyne measurements developed in this research can be directly applied to large-scale cluster state generation^11,37 using only squeezed light sources, beamsplitter network and homodyne measurements. Although the experimental complexity increases in large-scale fast cluster state generation, all the fundamental technologies have already been developed by this research. Therefore, this research is the first step for paving the way towards the high-speed generation of large-scale cluster states.

Regarding higher speed, the electrical system is the current limiting factor. In particular, the 1.85 mm connectors (V connectors) of the electrical components in the measurement system limit the bandwidth of the measurement up to 60 GHz and the timescale of EPR correlations to tens of picoseconds. The generation part, on the contrary, is much broader as the bandwidth of the squeezed light source is about 6 THz (ref. ³¹). Therefore, even with the same setup, higher-speed EPR correlations can be measured by increasing the bandwidth of the measurement system. Even with current commercially available optical communication technology, we expect a bandwidth extension of up to about 100 GHz to be readily achieved. The full usage of the terahertz-bandwidth quantum entanglement and femtosecond-timescale measurement might also be achieved in the future by combining the wavelength-division-multiplexing technique³⁸.

Finally, we discuss the possibility of EPR state generation and measurement with stronger correlation. First, the efficiency of the EPR state preparation η_state and measurement η_meas can be estimated from the efficiency of the individual component as η_state = 94%, η_meas (G = 1 (0 dB)) = 19% and η_meas (G ≈ 300 (25 dB)) = 76%. These values match the result of the experimental fitting (Methods). Towards further purification of the EPR states, the coupling from free space to the waveguide OPAs, which is the largest imperfection in the measurement system η_meas, is expected to be improved. By optimizing the alignment, the measurement efficiency η_meas can be increased from the current efficiency of 80% to more than 95% (ref. ²⁹). Once the coupling efficiency is improved, the next limit would be the squeezing level of the waveguide OPA, which is currently 8.3 dB (ref. ³¹). As the intrinsic loss of the OPA—for both state preparation and measurement—is roughly proportional to the waveguide length, shortening the crystal length will improve the efficiency at the cost of requiring higher pump power.

In conclusion, this research demonstrates the real-time observation of picosecond-timescale two-mode quantum entanglement. The observed EPR states show the quantum correlation of more than 4.5 dB with a wavepacket of 40 ps period. Our scheme will be the fundamental technology for paving the way to a wide range of ultrafast optical QIP applications.

Methods

Figure 2 shows the experimental setup. The fundamental laser is a continuous-wave laser at wavelengths of 1,545 nm and 772.5 nm. We utilize periodically poled lithium niobate waveguide OPAs³⁹ we developed as both a squeezed light source and a phase-sensitive optical amplifier.

The details of η_state and η_meas are as follows. The efficiency of the state preparation η_state is determined by the propagation efficiency (98%), the escape efficiency of the generation OPAs (96%)³⁹ and the interferometric visibility at the first beamsplitter (99.5%). By contrast, the efficiency of the measurement system η_meas without amplification (G = 1 (0 dB)) is determined by the coupling efficiency from free space to the fibre at the measurement OPAs (90%) and homodyne detector (90%), interferometric visibility at the homodyne measurement (99.6%) and efficiency of the broadband homodyne detector (36%). We numerically fit the efficiency of the system using two parameters: the efficiency before and after light enters the measurement OPAs. From the experimental parameters, we expect this to be around 70% and 20%, respectively. The corresponding fitting results are 68% and 16%, which are in agreement with the experimental parameters (Supplementary Information provides the details of the fitting). The pump power of the generation and measurement OPAs are 200 mW and 800 mW (measured after the OPAs), respectively. At this parameter, the gain of the measurement OPAs is about 25 dB. The local oscillator power is set to 45 mW, resulting in the clearance between shot noise and circuit noise to be more than 15 dB up to 20 GHz, and more than 10 dB up to 60 GHz.

The details of the measurement system are as follows. The output of the homodyne detector (BPDV3120R, Finisar) is amplified with 22 dB gain by the amplifier (M804C, SHF). After amplification, the signal is divided into two parts, one for the oscilloscope (Infiniium UXR-Series, Keysight) and the other for the phase-locking system. The bandwidth of the homodyne detectors is 70 GHz and the efficiency is 36%. The bandwidth of the amplifiers is from 90 kHz to 66 GHz. The bandwidth of the oscilloscope is 113 GHz and the sampling frequency is 256 gigasamples per second. We take 5,000 frames of data with 5,121 points each. The components are connected by a 1.85 mm connector (V connector), and their bandwidth of 66 GHz limits the bandwidth of the whole measurement.

In this experiment, we implemented seven phase lockings: the phases of the two squeezed light instances, the interference phase between the two squeezed light instances, the amplification phases at the measurement OPAs and the phases of the local oscillator light at the homodyne detectors. We use strong classical probe light injected from the generation OPAs to implement these phase lockings. Phase locking is performed by detuning the two probe lights from the fundamental frequency by 0.8 and 0.5 MHz, and observing the beat signal. Note that the interference at the beamsplitter in the EPR state generation uses the beat signal between the two probe lights. Therefore, the two probe lights require different amounts of frequency shift. The probe light is a strong classical light and it can disturb the quantum measurement; therefore, we separate phase control and measurement timing in the time domain. This means that all of the probe light is switched off during the measurement timing and only the pump light and local oscillator light are incident. The frequency detuning and the ON–OFF switching of the probe light is conducted by three acousto-optic modulators (AOMs). In this experiment, one cycle is 400 μs, out of which the control phase is 360 μs and the measurement phase is 40 μs.

Data availability

The experimental data used in this study are available via Dryad at https://doi.org/10.5061/dryad.dbrv15fbq.