In intense electromagnetic fields the vacuum state is unstable and spontaneously generates electron-positron (
High Power Laser Science and Engineering, Volume. 8, Issue 4, 04000e38(2020)
Asymmetric pulse effects on pair production in polarized electric fields

Using the Dirac–Heisenberg–Wigner formalism, effects of the asymmetric pulse shape on the generation of electron-positron pairs in three typical polarized fields, i.e., linear, middle elliptical and circular fields, are investigated. Two kinds of asymmetries for the falling pulse length, short and elongated, are studied. We find that the interference effect disappears with the shorter pulse length and that the peak value of the momentum spectrum is concentrated in the center of the momentum space. In the case of the extending falling pulse length, a multiring structure without interference appears in the momentum spectrum. Research results show that the momentum spectrum is very sensitive to the asymmetry of the pulse as well as to the polarization of the fields. We also find that the number density of electron-positron pairs under different polarizations is sensitive to the asymmetry of the electric field. For the short falling pulse, the number density can be significantly enhanced by over two orders of magnitude. These results could be useful in planning high-power and/or high-intensity laser experiments.
1 Introduction
The Schwinger effect is one of the nonperturbative phenomena in QED, while the understanding of it is still far from complete. Therefore, studying pair production in the nonperturbative regime would deepen our knowledge about the relatively less tested branch of QED. Motivated by this, many exploratory studies of the Schwinger effect based on a number of different theoretical techniques have been undertaken, for example, within the quantum kinetic approach[
In this paper we further investigate the Schwinger effect by considering the asymmetric pulse shape with Gaussian envelope and different polarizations. We mainly consider asymmetric pulse shape effects on pair production in different polarizations, e.g., linear, elliptic and circular polarizations. We reveal some novel features of the momentum spectra of created pairs for differently polarized electric fields. In this study the real-time DHW formalism is employed as it leads to efficient calculations in the case of a circularly[
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
This paper is organized as follows. In Section 2 we introduce the model of a background field. In Section 3 we briefly introduce the DHW formalism that is used in our calculations for completeness. In Section 4 we show the numerical results for momentum spectra and analyze the underlying physics. In Section 5 we give the numerical results for the pair number density. We end the paper with a brief summary and discussion in Section 6.
2 External electric field model
We focus on the study of
 (1)
(1)where
The main interest in this study is asymmetric pulse duration effects on pair production in differently polarized and time-dependent asymmetric electric fields. We mainly consider two different situations when the rising pulse length
3 Brief outline of the DHW formalism
The DHW formalism is an approach used to describe the quantum phenomena of a system by a Wigner function as the relativistic phase space distribution. It has also been further adopted in the studies of Sauter-Schwinger QED vacuum pair production[
A convenient starting point is the gauge-invariant density operator of two Dirac field operators in the Heisenberg picture
 (2)
(2) (3)
(3)The important quantity in the DHW method is the covariant Wigner operator, given as the Fourier transform of the density operator (Equation (2)):
 (4)
(4)By taking the vacuum expectation value of the Wigner operator, we obtain the Wigner function
 (5)
(5)For numerical convenience, the Wigner function can be decomposed into a complete basis set
 (6)
(6)Here
 (7)
(7) (8a)
(8a) (8b)
(8b) (8c)
(8c)Inserting decomposition (Equation (6)) into the equation of motion, Equation (7), for the Wigner function, we obtain a set of partial differential equations (PDEs) for the 16 Wigner components. Furthermore, for spatially homogeneous electric fields like Equation (1), by using the characteristic method[
 (9)
(9)For detailed derivations and explicit forms of these 10 equations, we refer the reader to Refs. [16, 17, 33]. Note that the corresponding vacuum nonvanishing initial values are
 (10)
(10)In the following, we express the scalar Wigner coefficient by the one-particle momentum distribution function
 (11)
(11) (12)
(12)So the one-particle momentum distribution function
 (13a)
(13a) (13b)
(13b) (13c)
(13c) (13d)
(13d)Finally, by integrating the distribution function
 (14)
(14)4 Momentum spectra of the produced particles
In this section we report some interesting results for the momentum spectra of the produced particles with several pulse parameters under typical cases of the polarization field, such as linear (
4.1 Linear polarization,
![]()
Figure 1.Momentum spectra of produced 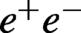 pairs for linear polarization (
pairs for linear polarization (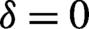 ) at
) at 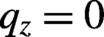 in the
in the 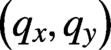 plane when the rising pulse length
plane when the rising pulse length 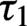 is fixed but the falling pulse length
is fixed but the falling pulse length 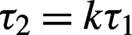 becomes shorter with
becomes shorter with 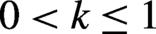 . The chosen parameters are
. The chosen parameters are 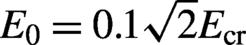 ,
, 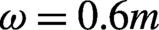 and
and 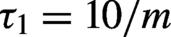 , where
, where 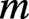 is the electron mass.
is the electron mass.
It can be seen that the momentum spectrum of the created pair is very sensitive to the asymmetry of the electric field. When the ratio parameter
 (15)
(15)Because of the fact that the vector potential vanishes at asymptotic times
![]()
Figure 2.Same as 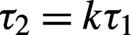 becomes longer with
becomes longer with 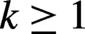 .
.
We find that the center maximum value of the momentum spectrum decreases until
 (16)
(16)after the considering of effective mass[
4.2 Elliptic polarization,
![]()
Figure 3.Same as 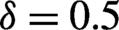 .
.
![]()
Figure 4.Same as 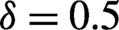 .
.
4.3 Circular polarization,
![]()
Figure 5.Same as 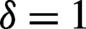 .
.
With decreasing
![]()
Figure 6.Same as 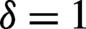 .
.

Table 1. The peak values of the particle distribution function
 for the typical polarization
for the typical polarization  when the rising pulse length
when the rising pulse length  is fixed and the falling pulse length
is fixed and the falling pulse length  is short and/or elongated. Note that these peaks occur at different values of the momentum
is short and/or elongated. Note that these peaks occur at different values of the momentum  .
.Table 1. The peak values of the particle distribution function
 for the typical polarization
for the typical polarization  when the rising pulse length
when the rising pulse length  is fixed and the falling pulse length
is fixed and the falling pulse length  is short and/or elongated. Note that these peaks occur at different values of the momentum
is short and/or elongated. Note that these peaks occur at different values of the momentum  .
.${f}_{\mathrm{max}}\left(\mathbf{q},\infty \right)$ $k=1$ $k=0.1$ $k=10$ $\delta =0$ $29.40\times {10}^{-6}$ $8.28\times {10}^{-4}$ $5.24\times {10}^{-5}$ $\delta =0.5$ $9.65\times {10}^{-6}$ $7.50\times {10}^{-4}$ $6.36\times {10}^{-5}$ $\delta =1$ $2.36\times {10}^{-6}$ $6.46\times {10}^{-4}$ $6.38\times {10}^{-5}$
5 Number density of pair production
![]()
Figure 7.The number density (in units of 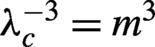 ) of pairs produced in differently polarized electric fields for the shorter falling length of the asymmetric pulse shape with
) of pairs produced in differently polarized electric fields for the shorter falling length of the asymmetric pulse shape with 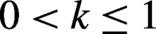 . The field parameters are the same as in
. The field parameters are the same as in 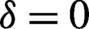 , elliptical
, elliptical 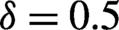 and circular
and circular 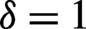 cases, respectively.
cases, respectively.
![]()
Figure 8.Same as 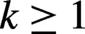 .
.
We find that, when the falling pulse width is shorter, i.e.,
Concretely, for linear polarization, the number density increases from
On the other hand, in the case of the elongated falling pulse, the number density of created pairs increases almost linearly with the field polarization parameter
From Figures 7 and 8, we can infer that the number density exhibits polarization dependence for shorter pulse asymmetry and elongated pulse asymmetry of the field. For shorter pulse asymmetry cases, the number density decreases with increasing field polarization, while for elongated pulse cases, the number density increases with increasing field polarization except for the case in which
In summary, when the falling pulse length is shortened, the number density can be increased by two orders of magnitude; however, when the falling pulse length is extended, the number density is enhanced to within only half orders of magnitude. Therefore, for asymmetric electric fields with different polarizations, in order to effectively increase the number density of the produced electron-positron pairs, it is better to shorten the falling pulse. Note that in our previous work on the linearly polarized case[
6 Summary and discussion
In this study we have investigated the effects of the asymmetric pulse shape on the momentum spectrum of created
When the falling pulse length is shorter, for linear polarization, the spectra of the produced pairs exhibit a shift and split of the peaks. For middle elliptic polarization as well as circular polarization, the momentum spectra become distorted and exhibit a shift of the peaks. Finally, for each different polarization, the peaks shifted to the central region in the momentum plane; therefore, peak values were enhanced by two orders of magnitude compared to the symmetric situation. When the falling pulse length is elongated, ring structures appear for different polarizations. We also noted that, for this asymmetric situation, the peak values increased with the field polarization compared to the symmetric case, but were smaller than in the shorter pulse cases. Some phenomena of the momentum spectra are consistent with the effect of frequency chirp[
We also studied the effect of asymmetric falling pulse on the obtained number density. We found that the number density decreases and/or increases with polarization for shorter and/or elongated falling pulses. It is important to note that, when the falling pulse is shorter, the number density of the produced pairs can be significantly enhanced by more than two orders of magnitude.
The results are helpful to understand the influence of the pulse duration, which is an important parameter of the external field, and to deepen our understanding of the external pulse structure. Although these results reveal some useful information about the production of
To understand why the multiphoton process is not obvious for shorter pulse cases
The other important phenomenon observed in our numerical results is the spiral structure in the momentum spectrum that has an intrinsic connection with the spin and/or orbital angular momentum of field photons as well as the produced
[1] F. Sauter. Z. Phys., 69(1931).
[2] W. Heisenberg, H. Euler. Z. Phys., 98(1936).
[3] J. S. Schwinger. Phys. Rev., 82(1951).
[4] F. Gelis, N. Tanji. Prog. Part. Nucl. Phys., 87(2016).
[5] T. Heinzl, A. Ilderton. Eur. Phys. J. D, 55(2009).
[6] M. Marklund, J. Lundin. Eur. Phys. J. D, 55(2009).
[7] O. J. Pike, F. Mackenroth, E. G. Hill, S. J. Rose. Nature Photon., 8(2014).
[8] A. Ringwald. Phys. Lett. B, 510(2001).
[9] R. Alkofer, M. B. Hecht, C. D. Roberts, S. M. Schmidt, D. V. Vinnik. Phys. Rev. Lett., 87(2001).
[10] C. D. Roberts, S. M. Schmidt, D. V. Vinnik. Phys. Rev. Lett., 89(2002).
[11] M. Orthaber, F. Hebenstreit, R. Alkofer. Phys. Lett. B, 80(2011).
[12] D. Vasak, M. Gyulassy, H. T. Elze. Annals Phys., 173(1987).
[13] I. Bialynicki-Birula, P. Górnicki, J. Rafelski. Phys. Rev. D, 44(1991).
[14] F. Hebenstreit, R. Alkofer, H. Gies. Phys. Rev. D, 82(2010).
[15] . Phys. Rev. Lett., 107(2011).
F. Hebenstreit, C. Kohlfürst, R. Alkofer, H. Gies. Eur. Phys. J. Plus, 133(2018).
[16] E. Akkermans, F. Hebenstreit, G. V. Dunne. Phys. Rev. Lett., 108(2012).
, arXiv:1106.5965 ().(2011).
[17] , arXiv:1512.06082 ().(2015).
C. K. Dumlu, C. Kohlfürst, G. V. Dunne. Phys. Rev. Lett., 104(2010).
[18] R. Schützhold, H. Gies, G. Dunne. Phys. Rev. Lett., 101(2008).
[19] F. Hebenstreit, R. Alkofer, G. V. Dunne, H. Gies. Phys. Rev. Lett., 102(2009).
[20] C. Kohlfürst, H. Gies, R. Alkofer. Phys. Rev. Lett., 112(2014).
[21] C. Kohlfürst, M. Mitter, G. von Winckel, F. Hebenstreit, R. Alkofer. Phys. Rev. D, 88(2013).
[22] O. Oluk, B. S. Xie, M. Bake, S. Dulat. Front. Phys., 9(2014).
[23] I. A. Aleksandrov, G. Plunien, V. M. Shabaev. Phys. Rev. D, 95(2017).
[24] B. S. Xie, Z. L. Li, S. Tang. Matter Radiat. Extremes, 2(2017).
[25] . Phys. Rev. D, 89(2014).
A. Blinne, A. Blinne, H. Gies, E. Strobel. Phys. Rev. D, 93(2016).
[26] A. Blinne. , arXiv:1701.00743 ().(2016).
[27] Z. L. Li, D. Lu, B. S. Xie. Phys. Rev. D, 92(2015).
[28] O. Olugh, Z. L. Li, B. S. Xie. Phys. Lett. B, 802(2020).
[29] O. Olugh, Z. L. Li, B. S. Xie, R. Alkofer. Phys. Rev. D, 99(2019).
Get Citation
Copy Citation Text
Obulkasim Olugh, Zi-Liang Li, Bai-Song Xie. Asymmetric pulse effects on pair production in polarized electric fields[J]. High Power Laser Science and Engineering, 2020, 8(4): 04000e38
Category: Research Articles
Received: Jul. 1, 2020
Accepted: Aug. 31, 2020
Posted: Sep. 2, 2020
Published Online: Nov. 23, 2020
The Author Email: Bai-Song Xie (bsxie@bnu.edu.cn)






