The rapid advancement of laser technology makes it possible to reach extremely high intensities in the laboratory[1], which in turn provides new insights into physics processes that have never been observed experimentally so far. Such a prospect motivates curiosity-driven scientific programs worldwide, complemented by a rapid transfer to industrial and societal applications[2].
High Power Laser Science and Engineering, Volume. 11, Issue 6, 06000e86(2023)
Zernike-coefficient extraction via helical beam reconstruction for optimization (ZEHBRO) in the far field

The spatial distribution of beams with orbital angular momentum in the far field is known to be extremely sensitive to angular aberrations, such as astigmatism, coma and trefoil. This poses a challenge for conventional beam optimization strategies when a homogeneous ring intensity is required for an application. We developed a novel approach for estimating the Zernike coefficients of low-order angular aberrations in the near field based solely on the analysis of the ring deformations in the far field. A fast, iterative reconstruction of the focal ring recreates the deformations and provides insight into the wavefront deformations in the near field without relying on conventional phase retrieval approaches. The output of our algorithm can be used to optimize the focal ring, as demonstrated experimentally at the 100 TW beamline at the Extreme Light Infrastructure - Nuclear Physics facility.
1 Introduction
Reaching the highest intensities systematically requires the concomitant maximization of the laser energy and minimization of the laser pulse duration as well as the surface area or laser spot size. This simple consideration has conditioned the development of short pulse lasers of larger and larger dimensions, from the original table-top solutions of the 1980s[3] to high-intensity lasers that fill buildings of the size of several sport halls[4]. Increasing the laser energy does not only come at the cost of a larger footprint of the laser; but also requires increasing the beam size to several tens of centimeters to keep the laser intensity below the damage threshold of its optical components. This renders large-scale facilities particularly susceptible to aberrations up to the point where active countermeasures have to be taken. For this purpose, modern laser systems employ adaptive optics (AO), yielding significant success in the optimization of the focal spot intensity. During the last decades, however, interest in experiments using tailored spatial intensity distributions in the far field (FF) arose as structured light with ultrahigh intensities grants access to a variety of experiments.
A sought-after beam profile is characterized by a central optical vortex, generating orbital angular momentum (OAM) in the beam, where an additional phase term in the form of
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
However, the practical implementation and experimental studies of such beams have encountered limitations, primarily due to the degradation of the intensity pattern in the FF[11]. Our investigations have shown that this degradation is caused by the high sensitivity of Laguerre–Gaussian-like beams to low-order angular wavefront (WF) aberrations, particularly when compared to regular beams without OAM[12]. Specifically, we have identified an increased sensitivity of the focus towards astigmatism, coma and trefoil in the Zernike-sense, which vary in angular direction.
Due to this high degree of sensitivity, conventional WF measurements in the near-field (NF) or ‘equivalent target plane’[13] approaches are hardly sufficient to optimize the ring shape in the focal plane. The main challenge here lies in the simultaneous action of non-common path aberrations and an increased sensitivity to those. The only way to circumnavigate this issue is to measure the phase directly in the FF. While phase retrieval[14] is traditionally used to tackle this issue, this approach is challenging to implement at high-intensity laser facilities as it requires high standards of the quality of the recorded data.
With the presence of OAM, however, the high sensitivity of the ring itself can be used to infer knowledge about the aberrations that are present in the NF. In this work, we propose and experimentally demonstrate a routine called Zernike-coefficient Extraction via Helical Beam Reconstruction for Optimization (ZEHBRO), which quickly retrieves low-order aberration coefficients from recordings of the FF fluence distribution to improve the control of beams with OAM. ZEHBRO uses a straightforward approach to retrieve quantitative information about the amplitude of the astigmatism, coma and trefoil in the NF of the beam and can thus aid the beam optimization in a more direct way than regular WF diagnostics.
The ZEHBRO method operates in two steps based on an intuitive approach that analyzes beam inhomogeneities and distortions. First, it extracts the ring intensity from the focus and obtains relevant descriptors using a fast Fourier transform (FFT). Second, it employs an iterative simulation process to find the Zernike coefficients that recreate these descriptors. This unique methodology relies solely on single FF measurements, eliminating the complications associated with non-common path aberrations commonly encountered in traditional WF sensing techniques, while still being significantly easier and faster than classical phase retrieval approaches. In the following, we first describe the beam characterization routine in detail. Afterwards, we present the findings of a numerical study in Section 3, which aimed at assessing the precision and robustness of this approach. Furthermore, we lay out some considerations that are relevant to the application of ZEHBRO in practice in Section 4. Lastly, we demonstrate the applicability of ZEHBRO in a real-world application, namely at the 100 TW beamline of the Extreme Light Infrastructure - Nuclear Physics (ELI-NP) high-intensity laser facility in Măgurele, Romania, and we discuss the limitations and advantages of this characterization method.
2 Zernike-coefficient extraction via helical beam reconstruction for optimization
In a previous work, we characterized the impact of low-order Zernike aberrations in top-hat circular beams with an OAM of
Regular approaches to WF optimization, for example, closed-loop AO with a wavefront sensor (WFS) in the NF, are only of limited use when these aberrations shall be eliminated in the FF with sufficient precision to maintain a homogeneous ring structure. This is mostly due to the presence of spatially varying optical path differences between the main and diagnostics arms, which is especially problematic for lasers with large beams that need downsizing in order to match the aperture of the WFS.
For this reason, we figured that the shape of the ring focus itself, and more specifically its uniformity, usually serve best as a reference for optimization. We decided to quantify this approach and develop a technique to directly extract a selection of Zernike aberrations from the FF of these beams without the necessity to implement a phase retrieval algorithm or the significant effort to set up a machine-learning-based AO loop[15], which are both much harder to do.
Specifically, we consider the Zernike aberrations with a Noll-index[16] from 5 to 10. This excludes the first four polynomials, as the piston and tip/tilt (indices 1–3) do not change the shape of the distribution, while defocusing (index 4) cannot be detected by the algorithm we are about to describe. Due to the self-similar diffraction of Laguerre–Gaussian beams, the latter does not deteriorate the ring shape and can thus be treated with regular optimization strategies. Throughout this paper, we will therefore write the corresponding coefficients for each WF in vectorial form:
In the following, we describe our extraction technique, which we call ZEHBRO. It mainly consists of two steps:
- (1)an analysis routine that extracts characteristic, scalar descriptors from an FF image;
- (2)an iterative routine which simulates an FF that recreates the extracted descriptors as closely as possible in order to retrieve the Zernike coefficients of low-order, angular aberrations.
2.1 Descriptor extraction
The first of the two core concepts of ZEHBRO is the extraction of a set of descriptors from a recording of the FF fluence. Ideally, each descriptor varies strongly with only one of the investigated aberrations and only weakly with the others. In this way, a quasi-diagonal transfer matrix between the descriptors and the Zernike base can be formulated, which greatly contributes to a fast convergence of the FF recreation, which we describe later.
In our previous work[12], we considered the ring intensity, that is, the intensity curve along the cusp of the ring focus, and described an algorithm to obtain it from real or simulated data (briefly summarized, this works by generating radial lineouts from the ring center and using bilinear interpolation to obtain the intensity at each peak position). In doing so, we found that the ring intensity varies periodically when pure angular aberrations are introduced. This is depicted in Figure 1 for astigmatism, coma and trefoil.
![]()
Figure 1.Simulated examples for the ring characterization in ZEHBRO for a Zernike coefficient of λ/20 (according to the Zernike normalization mentioned in the text) of astigmatism (left), coma (center) and trefoil (right). The WF map is shown in the top row and the corresponding FF below. The black line indicates the position for the ring intensity extraction, which is shown in the third row. The last row shows the absolute values of the first four FFT coefficients of the ring intensity, which can be rearranged to the descriptor vector (bottom).
The FFT of the normalized ring intensity reflects this behavior, where the amplitude and phase of these oscillations can be found in the first three non-zero-frequency coefficients. When split into the real and imaginary parts and reordered appropriately (see the bottom of Figure 1), we obtain a descriptor vector
In order to judge if these descriptors are suitable, that is, one descriptor reflects the amplitude of the associated Zernike aberration as purely as possible, we extracted the descriptors for simulated focal rings under varying amounts of pure Zernike aberrations. Figure 2 shows the results for the considered aberrations. The coefficients correspond to the normalization where
- •First, each descriptor varies approximately proportional to the associated aberration around the aberration free case, while there is no proportionality for any of the other descriptors.
- •Second, the linear behavior only exists very close to the aberration free case. Beyond that, nonlinear behavior or mixing with different descriptors occurs.
![]()
Figure 2.The descriptor values for simulated donut foci under a varying amount of each of the six pure Zernike aberrations considered by ZEHBRO. The gray dashed line shows the slope in the origin, belonging to the descriptor associated with the aberration whose amplitude varies along the
This already indicates that a linear transfer from the descriptor space to the Zernike space cannot be done. Furthermore, nonlinear mixing between the descriptors may occur when more than one Zernike aberration is present, occluding the real composition of the aberrations in the NF. Therefore, a more advanced approach is necessary to extract the coefficients from the FF.
2.2 Iterative FF reproduction
A straightforward approach for this step is to simulate focal rings with a measured intensity distribution in the NF and an assumption for the Zernike coefficients (e.g., all zero) and change the coefficients in an iterative manner until the descriptors of the simulated focal spot match the descriptors of the recorded focal spot. Here, the new estimation of each iteration can be done using the knowledge of the descriptor slopes around the origin, as depicted in Figure 2 with dashed lines. Using a vector of the reciprocal of these gradients
While the convergence of this algorithm is not guaranteed in general due to the nonlinear properties of this problem, it usually takes only a few iterations to converge as long as the ring shape of the focal spot is clearly visible.
3 Robustness
One of the essential aspects of the proposed method is its ability to converge as long as a ‘ring’ can be identified upon visual inspection of the FF. In order to judge the robustness of ZEHBRO, we simulated different scenarios and compared the output with the known input aberrations. For each scenario, we simulated a circular top-hat beam with an OAM of
Afterwards, we propagated the wave field to the FF using an FFT and emulated measurements with different experimental setups by moving and scaling the fluence distribution to a random position and size via interpolation. Furthermore, we added Poisson noise to the image to approximate different signal-to-noise ratios (SNRs), and converted the array to an 8-bit image, normalized to the maximum value.
Every data point of the graphs given in this section corresponds to the average RMS error, named
3.1 SNR
First, we investigated the robustness of ZEHBRO against camera noise (i.e., the aggregate of photon noise, readout noise, etc.). We define the SNR as follows:
The result of this study is shown in Figure 3. Obviously, the impact of the SNR remains small above an SNR of approximately 20, with no significant impact of higher SNRs for any of the considered aberration amplitudes. This is expected, as the spatially uncorrelated nature of Poisson noise primarily contributes to high spatial frequencies in the ring intensity, while ZEHBRO only considers the first three frequency components.
![]()
Figure 3.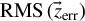 for different SNR values, considered at three different input aberration amplitudes. The ring diameter was set to 15 pixels and
for different SNR values, considered at three different input aberration amplitudes. The ring diameter was set to 15 pixels and 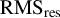 to 0.0125λ.
to 0.0125λ.
However, ZEHBRO abruptly fails at lower SNRs, generating large errors. This behavior originates in the algorithm for the ring-center determination, which fails due to thresholding that is inadequate for high noise levels. A more elaborated approach, for example, using a correlation function, could potentially work even in lower SNR scenarios.
3.2 Ring diameter
Furthermore, we investigated the impact of the ring diameter in relation to the sample size of the sensor. For this test, we generated the FFs with fixed ring diameters for each data point and calculated the mean error for different amounts of disturbance in terms of the SNR and
![]()
Figure 4.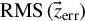 over the ring diameter in pixels for scenarios featuring different amounts of disturbance defined by combinations of varying SNRs and
over the ring diameter in pixels for scenarios featuring different amounts of disturbance defined by combinations of varying SNRs and 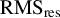 values.
values.
Surprisingly, the ring diameter has only a small impact on the precision of ZEHBRO. Compared to the impact of the other disturbance, we could not identify any significant trend, even for the smallest considered ring diameter of only 6 pixels. We therefore conclude that ZEHBRO is feasible for any setup that images a decently resolved FF.
However, a strong correlation between the amplitude of the higher order aberrations and the error becomes apparent when considering the base level of the three curves.
3.3 Aberration amplitude and higher order aberrations
Therefore, we investigated the interplay between the amplitude
![]()
Figure 5.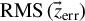 for different total input aberration amplitudes
for different total input aberration amplitudes 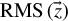 under the presence of a varying
under the presence of a varying 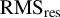 of random higher order aberrations.
of random higher order aberrations.
Considering this graph, the range of application of ZEHBRO becomes more pronounced: first of all, the nonlinear properties of the problem, that is, the Fourier transform being a nonlinear transfer from the NF to the FF, limiting the quasi-linear and unique relation between the descriptors and the Zernike coefficients of the aberrations to a small amplitude range, become already apparent when only considering the case of
The second observation is that the error rises with increasing numbers of high-order aberrations
While the demand for precision may be driven by the application, we can still formulate a rule of thumb for the range in which ZEHBRO can be applied for regular optimization tasks:
- •aberrations
$\mathrm{RMS}\left(\vec{z}\right)$ - •high-order aberrations
${\mathrm{RMS}}_{\mathrm{res}}$
In a real-life scenario, however, it may be hard to distinguish between
4 Zernike-base transfer
Aside from the general range of validity for ZEHBRO, there is another issue that has to be addressed in order to use the output for optimization of the FF, which we discuss in this section. This is because ZEHBRO estimates a set of six Zernike coefficients from an image of an FF only, which is only possible due to several underlying assumptions, for example, the intensity profile in the NF and the orientation of the Zernike base in the NF, which is assumed to align with the orientation of the FF camera.
While the NF intensity can be set by using an actual recording of the beam profile, the orientation, as well as the Zernike-normalization method used by ZEHBRO, may differ from other base definitions in the system, for example, the one used for modal control of a deformable mirror (DM). For this reason, it may be useful to experimentally record a transfer matrix
where
Here,
On the other hand, these mixing matrices should be zero if a good overlap between the pupil definitions is given. In fact, we recommend enforcing these terms to be zero if the recording of reference points for the calculation of
5 Experimental validation
The experimental validation of the beam optimization method ZEHBRO took place at the ELI-NP facility, more precisely on the 100-TW arm, as depicted in Figure 6. There, a diagnostic bank is installed directly after the compressor in the main laser hall, before the beam transports to the 100-TW experimental area E4. Among other things, the diagnostic bank features a Shack–Hartmann WFS (M PLQ HASO4 FIRST 0919 by Imagine Optic) and FF camera (acA1300-60gm by Basler, delivering 8-bit images), which aid the control of the DM (ILAO Star by Imagine Optic, 30 mm pupil, 25 actuators) and inspect the beam focus quality, respectively. At this location, the beam line features a nominal beam diameter of 55 mm, a repetition rate of 10 Hz and a pulse energy of up to 2.3 J within 24 fs at a central wavelength of 808 nm and a bandwidth of 57 nm.
![]()
Figure 6.Experimental setup at the ELI-NP facility for the validation of ZEHBRO.
The first step towards the validation at the ELI-NP facility was to have an implementation of ZEHBRO that could be used in the laboratory environment, meaning being able to interface quickly to the cameras used for the beam diagnostics. For this, we used the Wavefront Optics Measurement and Beam Analysis Tool (WOMBAT)[17], our open source modular vision and laser metrology software. (The community edition of WOMBAT is available on the GSI Gitlab repository:
![]()
Figure 7.Screenshot of the ZEHBRO module in WOMBAT: (a) camera view (live) with overlays indicating the sampling positions; (b) extracted ring intensity; (c) reproduced FF view; (d) retrieved Zernike coefficients.
Back to the beamline, a transmitting helical phase plate with 16 discrete levels is inserted in the beam in order to obtain the ‘donut’ beam, using a motorized translation stage. The phase plate is manufactured from fused silica and optimized for the central wavelength of the beam. Due to the wavelength dependence of the material, the outer parts of the spectrum experience a non-perfect helix. For example, at the point where the spectrum hits
For obvious reasons, the phase plate must be installed before the compressor to avoid nonlinear effects with the temporally compressed pulse[18]. In addition, the maximum allowed energy was reduced to 1 J to keep intensity modulations, caused by the phase discontinuity of the phase plate, below the damage threshold of the compressor gratings and components in the following laser beamline.
The first step in the optimization process takes place without the phase plate and deals with a standard optimization between the DM and the WFS. This step is part of the optimization routine of the laser, which is repeated at regular intervals whenever a realignment of the laser chain needs to be done. Its goal is to provide a nearly flat WF at the WFS to start with, as we have shown that ZEHBRO can only take over when the beam aberrations are already small. This step was repeated by the ELI-NP operation team on the day of the experiment. After this step, the FF intensity distribution of the beam exhibited a good agreement with the calculated Strehl ratio of the WFS, qualitatively. The corresponding FF is shown in Figure 8(a).
![]()
Figure 8.FF distributions at the compressor sensor. The images were created by centering and averaging 300 images, equal to 30 seconds of operation: (a) the FF prior to the insertion of the spiral phase plate; (b) after insertion of the phase plate; (c) after conventional manual optimization; (d) after optimization using ZEHBRO.
For the second step, the phase plate was brought into the beam. The image of the FF, shown in Figure 8(b), clearly showed deformations in the intensity distribution that can be attributed to several factors. First of all, the calibration of the WFS was likely only accurate with respect to regular beams, where the errors only became visible once OAM was introduced to the beam, making the FF more sensitive to aberrations. A second possible factor is the limited convergence precision of the AO feedback loop due to calibration errors and/or fluctuations in time. Third, we cannot rule out a contribution from spatial phase distortion introduced by the phase plate itself. In addition, the FF intensity distribution showed a stronger level of fluctuation than without the phase plate, showing again that small WF fluctuations can have larger effects on beams with OAM than on beams without OAM. This can be clearly seen in the single-shot samples of the FF in different optimization steps in Figure 9, as well as in the animated plots in the
![]()
Figure 9.The RMS of the deviation from an ideal, homogeneous ring intensity, calculated using
After the phase plate insertion, we performed another traditional, manual optimization of the Zernike coefficients to test the limits of this approach. The optimization was limited to single-term optimization on a trial-and-error basis, which was inspired by the intuitive understanding of the effect of low-order Zernike aberrations on the ring intensity. However, this process was lengthy and not accurate due to an unknown transfer matrix between the Zernike basis of ZEHBRO and the DM at this point, as well as the strong fluctuations in the ring intensity. Overall, the optimization took more than 30 min and yielded the beam shown in Figure 8(c). Figure 10 (left) shows the quantitative analysis of the ring intensity of this beam.
![]()
Figure 10.Statistics of the ring intensity of the FF distributions as shown in
The third step was to have a full closed-loop with ZEHBRO including the projection of the Zernike coefficients from ZEHBRO into the Zernike base of the DM control matrix, as described in Section 4, via Equation (2). After recording
As shown by the intensity distribution image in Figure 8 as well as in the
![]()
Figure 11.Statistics of the Zernike coefficients as returned by ZEHBRO after the manual optimization and the optimization based on the output of ZEHBRO, using the Zernike-projection technique. The dataset is identical to the one used in
As a quantitative measurement of the quality improvement of the ring, we calculated the normalized ring RMS:
In doing so, we obtained a
6 Discussion and outlook
In this work, we developed ZEHBRO, an intuitive and super-sensitive low-order angular WF sensing technique for beams with an OAM of
However, there are limitations on the range of application. First, our investigations showed that ZEHBRO only works well on beams that are already well corrected in a traditional sense (rule of thumb, WF-RMS
It should also be noted that we did not investigate this approach for beams with an OAM of l > 1, which is something to be done in the future. We tested our routine experimentally at the compressor output of the 100 TW beamline at the ELI-NP facility for the optimization of a ring focus. Here, we were able to demonstrate a fast convergence and better precision compared to traditional, manual optimization. However, the precision was greatly limited due to beam fluctuations caused by air turbulence in the system. This is due to the large sensitivity of the donut to angular aberrations, which reveals small disturbances in the otherwise remarkably stable beam. With a more static WF and the possibility to programmatically interface with the DM control software, we expect a much greater precision in the optimization routine.
As there are other techniques that enable measuring the NF phase in the FF for optimization, a brief comparison is due. First, there is the family of genetic algorithms (GAs). These rely on the definition of a fitness-function (e.g., the Strehl ration) that is used to judge the quality of a batch of guesses for the WF, called a generation. In each generation, a selection of the best guesses is used to derive the next generation. This approach is conceptually easy, does not rely on any knowledge of the beam and has been proven to be functional in a wide range of experimental conditions. Recently, it has been successfully demonstrated that a GA can also be used for the optimization of a beam carrying OAM[20]. However, GAs are usually slow in convergence and are thus sensitive to beam drifts and fluctuations.
Second, there is the ongoing research about phase retrieval algorithms[14]. Here, several images around the focal region are used to retrieve the NF phase in an iterative manner[21]. These approaches can retrieve aberrations up to large amplitudes and spatial frequencies and are nowadays available in commercial software. Due to the recording of the data in a narrow time window, beam drifts are not a problem for phase retrieval. However, phase retrieval algorithms tend to be sensitive to the coherence of the recorded images and can thus be easily impaired by fast beam fluctuations and STCs. Furthermore, the retrieval of the phase requires a large number of iterations compared to ZEHBRO, which renders this type of measurement useless for real-time applications.
Third, there is the rising field of machine learning[22]. There are vastly different approaches here, but many of them include the usage of phase masks that generate an extended diffraction pattern in the FF in order to collect more data about the phase[23], or even implement diffractive neural networks in front of the FF sensor[24]. Then, a model is trained on a large collection of known data points in order to be able to make single-shot estimations of the NF phase. These approaches have been proven to be versatile, even granting insight into STCs, and provide fast phase estimations once the training has been successfully completed[23]. However, the generation of such a model is challenging in many aspects, including the loss of intuitive understanding about the beam and the recording of a suitable and sufficiently large dataset for training and verification. Furthermore, these models do not (yet) generalize well to be used in a wider range of experimental conditions.
This comparison emphasizes the use of ZEHBRO within its own niche due to its simplicity, speed, sensitivity and system-independent validity. In these terms, ZEHBRO is ready to take the leap into the realm of real-world applications, while other methods still need either expert knowledge or further research to be of practical use.
One of the primary advantages of optimization of the ring focus using ZEHBRO compared to phase retrieval becomes apparent when off-axis focusing is used, for example, using an off-axis parabolic (OAP) mirror. Focusing like this has an impact on the NF distribution prior to the propagation towards the FF: one side of the NF is contracted, increasing the flux and the WF gradients, while the other side dilates, decreasing flux and WF gradients[25]. The result is that the amount of deflection caused by the OAM is stronger on one side of the beam compared to the other, leading to a bias towards one side of the focal ring distribution. This effect becomes worse with larger off-axis angles and smaller F-numbers and is practically indistinguishable from the impact of the coma on the FF (compare Figure 1, second image of the second row). As such, this distribution can be counteracted by introducing a setup-dependent amount of coma in the NF, generating a homogeneous ring once more. This underlines the strength of ZEHBRO in optimizing the ring intensity, as conventional approaches can only achieve this via calculations based on other assumptions to get to this point.
Looking towards the future, it is planned to integrate ZEHBRO in the ELI-NP laser system for advanced beam control. This means that the whole process has to be accelerated, where the goal is to automate the recording of the Zernike-transfer matrix
Another possibility would be to replace the focal ring recreation part of ZEHBRO with a direct interface to the DM modes, which would greatly increase the speed of ZEHBRO, remove the necessity for a Zernike transfer and reduce the whole procedure to a linear feedback loop not unlike a traditional AO loop. This would come at the cost of not knowing the composition of the NF aberrations as a whole, but would likely grant a better convergence towards a homogeneous ring due to a smaller number of error sources in the chain. Furthermore, a possible pathway would be to apply machine learning to images of the FF in order to gain insight into higher order aberrations. At the same time, this could potentially alleviate the limitations due to the nonlinearity of the problem and make machine-ZEHBRO applicable in a larger range of aberration amplitudes while still featuring the sensitivity gained from using helical beam.
[1] J. W. Yoon, Y. G. Kim, I. W. Choi, J. H. Sung, H. W. Lee, S. K. Lee, C. H. Nam. Optica, 8, 630(2021).
[2] G. A. Mourou, T. Tajima, S. V. Bulanov. Rev. Mod. Phys., 78, 309(2006).
[3] P. Maine, D. Strickland, P. Bado, M. Pessot, G. Mourou. IEEE J. Quantum electron., 24, 398(1988).
[4] F. Lureau, G. Matras, O. Chalus, C. Derycke, T. Morbieu, C. Radier, O. Casagrande, S. Laux, S. Ricaud, G. Rey, A. Pellegrina, C. Richard, L. Boudjemaa, C. Simon-Boisson, A. Baleanu, R. Banici, A. Gradinariu, C. Caldararu, B. De Boisdeffre, P. Ghenuche, A. Naziru, G. Kolliopoulos, L. Neagu, R. Dabu, I. Dancus, D. Ursescu. High Power Laser Sci. Eng, 8, e43(2020).
[5] L. Hu, T. Yu, Y. Lu, G. Zhang, D. Zou, H. Zhang, Z. Ge, Y. Yin, F. Shao. Plasma Phys. Controll. Fusion, 61, 025009(2018).
[6] J. Vieira, J. T. Mendonça. Phys. Rev. Lett., 112, 215001(2014).
[7] G. Pariente, F. Quéré. Opt. Lett., 40, 2037(2015).
[8] R. Nuter, P. Korneev, I. Thiele, V. Tikhonchuk. Phys. Rev. E, 98, 033211(2018).
[9] J. L. Martins, J. Vieira, J. Ferri, T. Fülöp. Sci. Rep., 9(2019).
[10] J. T. Mendonça, J. Vieira. Phys. Plasmas, 21, 033107(2014).
[11] C. Brabetz, S. Busold, T. Cowan, O. Deppert, D. Jahn, O. Kester, M. Roth, D. Schumacher, V. Bagnoud. Phys. Plasmas, 22, 013105(2015).
[12] J. B. Ohland, U. Eisenbarth, M. Roth, V. Bagnoud. Appl. Phys. B, 125(2019).
[14] C. Guo, C. Wei, J. Tan, K. Chen, S. Liu, Q. Wu, Z. Liu. Opt. Lasers Eng., 89(2017).
[15] Y. Guo, L. Zhong, L. Min, J. Wang, Y. Wu, K. Chen, K. Wei, C. Rao. Opto-Electron. Adv, 5, 200082(2022).
[16] R. J. Noll. J. Opt. Soc. Am., 66, 207(1976).
[17] J. B. Ohland, U. Eisenbarth, C. Brabetz, V. Bagnoud, M. Roth. 8th Conference of the International Committee on Ultrahigh Intensity Lasers(2018).
[18] V. Iancu, M. Talposi, S. Popa, P. Ghenuche, M. Cernaianu, D. Doria, G. Cojocaru, I. Dancus, R. Ungureanu, O. Chalus, D. Ursescu. Adaptive Optics and Applications, OTh4B-2(2022).
[19] A. Talposi, V. Iancu, D. Ursescu. Photonics, 9, 389(2022).
[20] M. Burger, J. M. Murphy, L. A. Finney, N. Peskosky, J. A. Nees, K. Krushelnick, I. Jovanovic. Opt. Express, 30, 26315(2022).
[21] R. W. Gerchberg. Optik, 35, 237(1972).
[22] G. Ju, X. Qi, H. Ma, C. Yan. Opt. Express, 26, 31767(2018).
[23] J. White, S. Wang, W. Eschen, J. Rothhardt. Opt. Express, 29, 9283(2021).
[24] E. Goi, S. Schoenhardt, M. Gu. Nat. Commun., 13, 7531(2022).
[25] J. B. Ohland, Y. Zobus, U. Eisenbarth, B. Zielbauer, D. Reemts, V. Bagnoud. Opt. Express, 29, 34378(2021).
Get Citation
Copy Citation Text
J. B. Ohland, D. Posor, U. Eisenbarth, V. Iancu, R. Ungureanu, D. Ursescu, V. Bagnoud. Zernike-coefficient extraction via helical beam reconstruction for optimization (ZEHBRO) in the far field[J]. High Power Laser Science and Engineering, 2023, 11(6): 06000e86
Category: Research Articles
Received: Jun. 21, 2023
Accepted: Jul. 26, 2023
Posted: Jul. 26, 2023
Published Online: Dec. 6, 2023
The Author Email: J. B. Ohland (j.b.ohland@gsi.de)






