In recent years, there has been an increased interest in the interaction of light with structured plasma. For example, plasma gratings may be used for short pulse amplification and the compression of high-power chirped pulses[1,2], transient plasma photonic crystals used as a high reflector[3], plasma-based optical components such as lenses, diffractive and holographic lenses[4–6], polarization optics[7–9], crossed-beam energy re-distribution for symmetry control in inertial confinement fusion (ICF)[10] and crossed-beam depolarization for mitigating parametric instabilities in ICF[11]. Currently, the efficiency of the above-mentioned applications is poor. One of the main reasons for the low efficiency of these schemes is the difficulty of controlling these plasma structures as they are driven into the nonlinear regime. To overcome this limitation, we proposed to drive a high-amplitude, standing ion acoustic wave (SIAW) by the interaction of a plasma medium with two counter-propagating laser beams that are amplitude modulated with a slowly varying frequency[12]. The beating frequency of the chirped two counter-propagating beams starts slightly off the linear resonance of an ion acoustic wave, and then slowly sweeps through it. If the chirp rate is slow enough, the plasma oscillations are automatically phase-locked to the beating frequency and stay in resonance. This process is known as autoresonance (AR). AR is a proven and general technique of exciting an oscillatory nonlinear system into high energies by a weak chirped driving oscillation[13–15]. This method is general and has been applied in many fields of physics, such as particle accelerators, coherent control of molecular vibration states[14–17], fluid dynamics[18], plasmas[19], nonlinear waves[20] and planetary dynamics[21].
High Power Laser Science and Engineering, Volume. 12, Issue 1, 010000e8(2024)
A GHz chirped amplitude-modulated laser for high-contrast plasma gratings
The generation and control of large amplitude plasma gratings and other plasma structures is of paramount importance for the realization of plasma photonics. Autoresonant excitation of such structures by means of chirped amplitude-modulated lasers has been recently discussed and analyzed theoretically. Here we discuss the parameter space for the realization of such a scheme and describe the laser system that was built towards this goal. We also expand our earlier theoretical study to account for the more realistic case of a moderately focused laser beam, instead of the simplified plane wave approximation.
1 Introduction
In this paper, we follow our previous theoretical proposal[12] and report on the development of a laser system to drive the SIAW and push it into the nonlinear regime where the amplitude of the acoustic wave could reach a significant fraction of the unperturbed plasma density. This laser is designed with the ability to arbitrarily modulate its amplitude with a modulation frequency of up to a few GHz. For the purpose of driving the SIAW into high energies, we chirped the amplitude modulation from about 500 MHz to more than 3.5 GHz. It is worth mentioning here that such a laser may be useful for other applications, such as the chirped amplitude modulation laser radar (LADAR) for range and Doppler measurements and for 3D imaging[22].
The paper is organized as follows. In Section 2, we analyze the parameter space for generating the SIAW and the required laser parameters. In Section 3, we describe our laser system. Next, with the analysis of Section 2 and the available laser parameters (Figure 1), we show that a moderate focusing of the laser is needed for attaining the AR threshold intensity, and our plane wave approximation in Ref. [12] might not be valid. In the Appendix, we take our previous plane wave approximation and extend it to the more realistic case of focused laser beams with a finite waist.
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
![]()
Figure 1.A selection chart for the best experimental conditions. (a) The pulse energy threshold (in mJ) as a function of the plasma density (in units of 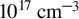 ), assuming a beam waist of
), assuming a beam waist of 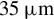 . (b) The time window
. (b) The time window 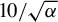 (in ns) as a function of the plasma density. (c) The swept bandwidth within the time window of 35 ns. (d) The linear ion acoustic wave frequency (GHz). The laser wavelength is chosen to be
(in ns) as a function of the plasma density. (c) The swept bandwidth within the time window of 35 ns. (d) The linear ion acoustic wave frequency (GHz). The laser wavelength is chosen to be 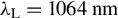 and the electron temperature is 0.5 eV. Orange and blue lines represent the ion mass of 20 a.u. (neon) and the dimensionless chirp rate of
and the electron temperature is 0.5 eV. Orange and blue lines represent the ion mass of 20 a.u. (neon) and the dimensionless chirp rate of 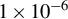 or
or 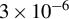 , respectively. Green and black lines represent the ion mass of 4 a.u. (helium) and the dimensionless chirp rate of
, respectively. Green and black lines represent the ion mass of 4 a.u. (helium) and the dimensionless chirp rate of 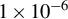 or
or 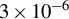 , respectively.
, respectively.
2 Parameter space of the experiment
In all autoresonant driving schemes, the driver frequency is slowly varying, passing through the zero-amplitude natural frequency of the system, and if the driving force exceeds a certain threshold, the nonlinear system is automatically phased-locked with the driver frequency. In that case, the resonance condition
To realize AR-driven SIAWs in the laboratory, we have to choose the right conditions, such as the plasma density, electron temperature, ion mass and driving frequency chirp rate, to fit within the experimental limitations. A prerequisite for the success of the experiment is a laser driver with intensity above the AR threshold. One way to keep this AR threshold low is to reduce the chirp rate,
We choose to set our laser wavelength at 1064 nm since both seeding lasers are abundant, fast electro-optical modulators are available and there are efficient neodymium-doped yttrium aluminum garnet (Nd:YAG) amplifiers. This wavelength choice imposes the wavelength of the ion acoustic wave to be half of the laser wavelength (
![]()
Figure 2.(a) Schematic of cavity design. M1, spherical front end-mirror with radius of 3 m; L1, 63 mm; PC, Pockels cell; L2, 60 mm; QWP, quarter waveplate; L3, 340 mm; L4, 10 mm; lens, focal length −750 mm; L5, 500 mm; Nd:YAG, gain medium; iM, removable flat mirror used as the back end-mirror of the short cavity; L6, 1.1 m; M2 and M3, spherical mirrors with radius of 2 m; L7, 2 m; L8, 1 m; M4, flat mirror used as the end-mirror of the long cavity. (b) Caustic of the beam inside the cavity obtained from simulations with ReZonator 2[24].
3 Laser system
According to our analysis in Section 2, our laser should have the following parameters: central wavelength
To reach the AR threshold, we have to amplify the shaped 3 nJ seed by about six orders of magnitude. A regenerative amplifier[23] could fill this energy gap while supporting a good beam profile. Nevertheless, the need for high pulse energy/high laser power and maintaining the required time structure of the pulse imposes some challenges. The first challenge is to inject the seed pulse into the regenerative amplifier, lock it inside the cavity and amplify it while preserving its shape and avoiding clipping it. In a common regenerative design[23] (see Figure 2(a)), the seed is reflected from a polarizer into the cavity, passing through a quarter waveplate (QWP) and a passive Pockels cell, reflected from the first end mirror of the cavity (M1) towards the second end mirror (M4). While going towards the second end mirror, it goes again through the passive Pockels cell and the QWP. Once the tail of the pulse passes the second time through the Pockels cell, it is possible to switch on the Pockels cell and lock the pulse inside the cavity, but care should be taken not to clip at this time the head of the pulse. Since our pulse duration is designed to be in the region of 35 ns, the distance from the Pockels cell to the second end mirror and back to the Pockels cell should be around 11 m. Such a long cavity poses difficulties in aligning it and keeping it stable. To extract high power out of it is even more challenging because of the thermal lensing effect. Figure 2(a) shows a schematic of our regenerative cavity. Our guidelines in the design of the cavity were as follows: (i) make it long enough to accommodate the approximately 35 ns pulse without clipping it; (ii) position the Pockels cell where the beam waist is large enough to avoid damages to the Pockels cell; (iii) position the gain medium (Northrop Grumman, diode-pumped, Nd:YAG rod, 2 mm diameter and length of 63 mm) where the beam waist is filling the entire Nd:YAG rod cross-section in order to extract as much energy as possible; (iv) the cavity should be stable for a large range of thermal lensing (see Figure 3); (v) there should be easy alignment of the cavity.
![]()
Figure 3.The cavity stability parameter as a function of the effective thermal lensing (black). The red lines indicate the limits of stability.
We used ReZonator 2[24] to analyze the caustic of the beam inside the cavity (Figure 2(b)) and the cavity stability as a function of the gain medium thermal lensing (Figure 3). To calculate the stability of the cavity with respect to the thermal lensing, we modeled the thermal lensing effect by virtually placing a lens inside the Nd:YAG rod with the focal length as a variable parameter and calculated the stability parameter
The cavity length as given in Figure 2 is 5.3 m. To align such a long cavity and find the optimal cavity arrangement is not easy. To overcome this problem, we used a modular approach. We first built a short cavity by inserting a flat-end mirror right after the gain medium (see the iM mirror in Figure 2(a)) and optimized the approximately 1 m long cavity. Once this cavity is perfected, we put an iris around the leaked beam from the flat-end mirror and imaged it with a 4f, 4-m long telescope on another flat mirror. With this flat mirror we retroreflect the beam back through the iris, then remove the iM mirror and form the 5.3 m long cavity.
Figures 4–6 show the chirped modulated signal from the AWG, along with the output from the regenerative amplifier. Comparing the AWG signal to the amplified optical pulse, we can see a slight square wave distortion of the envelope in which the tail of the pulse experiences a lower gain than the head of the pulse.
![]()
Figure 4.Electronic signal from the AWG (top) chirped from 1 to 0.77 GHz, and amplified optical pulse at 400 Hz repetition rate and averaged power of 910 mW.
This distortion could be compensated by shaping the pulse with the AWG, but it is not really important for the purpose of AR excitation since the AR threshold is mainly important at the beginning of the pulse. Besides this distortion, we see that the amplitude modulated high frequencies and the chirp rate are well preserved during the six-order of magnitude amplification. The average output power is about 1 W at the optimal repetition rate of 400 Hz, that is, about 2.5 mJ/pulse.
![]()
Figure 5.The same as
![]()
Figure 6.The same as
If we look at the AR threshold conditions that are given in Figure 1 we see that 2.5 mJ per pulse would be enough if we focus the beam into a spot size of
![]()
Figure 7.The ratio between the AR threshold for the finite beam width to the AR threshold for the case of a plane wave. Here,
To conclude, we have analyzed the available parameter space for the AR excitation of nonlinear ion acoustic waves and built the required chirped amplitude-modulated laser that could drive the ion acoustic waves. The shape of the laser pulses is determined by an AWG with pulse duration spanning from a few ns to approximately 30
[1] V. M. Malkin, G. Shvets, N. J. Fisch. Phys. Rev. Lett., 82, 4448(1999).
[2] A. A. Andreev, C. Riconda, V. T. Tikhonchuk, S. Weber. Phys. Plasmas, 13, 053110(2006).
[3] G. Lehmann, K. H. Spatschek. Phys. Rev. Lett., 116, 225002(2016).
[4] Y. Katzir, Y. Ferber, J. R. Penano, R. F. Hubbard, P. Sprangle, A. Zigler. Opt. Express, 21, 5077(2013).
[5] I. Y. Dodin, N. J. Fisch. Phys. Rev. Lett., 88, 165001(2002).
[6] M. R. Edwards, V. R. Munirov, A. Singh, N. M. Fasano, E. Kur, N. Lemos, J. M. Mikhailova, J. S. Wurtele, P. Michel. Phys. Rev. Lett., 128, 065003(2022).
[7] P. Michel, L. Divol, D. Turnbull, J. D. Moody. Phys. Rev. Lett., 113, 205001(2014).
[8] D. Turnbull, P. Michel, T. Chapman, E. Tubman, B. B. Pollock, C. Y. Chen, C. Goyon, J. S. Ross, L. Divol, N. Woolsey, J. D. Moody. Phys. Rev. Lett., 116, 205001(2016).
[9] G. Lehmann, K. H. Spatschek. Phys. Rev. E, 97, 063201(2018).
[10] P. Michel, L. Divol, E. A. Williams, S. Weber, C. A. Thomas, D. A. Callahan, S. W. Haan, J. D. Salmonson, S. Dixit, D. E. Hinkel, M. J. Edwards, B. J. MacGowan, J. D. Lindl, S. H. Glenzer, L. J. Suter. Phys. Rev. Lett., 102, 025004(2009).
[11] Y. X. Wang, S. M. Weng, P. Li, Z. C. Shen, X. Y. Jiang, J. Huang, X. L. Zhu, H. H. Ma, X. B. Zhang, X. F. Li, Z. M. Sheng, J. Zhang. High Power Laser Sci. Eng, 11, e37(2023).
[12] L. Friedland, G. Marcus, J. S. Wurtele, P. Michel. Phys. Plasmas, 26, 092109(2019).
[13] J. Fajans, L. Frièdland. Amer. J. Phys., 69(2001).
[14] G. Marcus, L. Friedland, A. Zigler. Phys. Rev. A, 69, 013407(2004).
[15] G. Marcus, L. Friedland, A. Zigler. Phys. Rev. A, 72, 033404(2005).
[16] G. Marcus, A. Zigler, D. Eger, A. Bruner, A. Englander. J. Opt. Soc. Am. B, 22, 620(2005).
[17] G. Marcus, A. Zigler, L. Friedland. Europhys. Lett., 74, 43(2006).
[18] L. Friedland. Phys. Rev. E, 59, 4106(1999).
[19] J. Fajans, E. Gilson, L. Friedland. Phys. Rev. Lett., 82, 4444(1999).
[20] L. Friedland, A. G. Shagalov. Phys. Rev. Lett., 81, 4357(1998).
[21] L. Friedland. Astrophys. J., 547, L75(2001).
[22] B. Stann, B. C. Redman, W. Lawler, M. Giza, J. Dammann, K. Krapels. Proc. SPIE, 6550, 655005(2007).
[23] W. Kochner. Solid State Laser Engineering(2006).
[25] L. D. Landau, E. M. Lifshitz. Mechanics(2011).
Get Citation
Copy Citation Text
Michael Valdman, Amir Hen, Gilad Marcus. A GHz chirped amplitude-modulated laser for high-contrast plasma gratings[J]. High Power Laser Science and Engineering, 2024, 12(1): 010000e8
Category: Research Articles
Received: Sep. 1, 2023
Accepted: Nov. 9, 2023
Published Online: Feb. 19, 2024
The Author Email: Gilad Marcus (gilad.marcus@mail.huji.ac.il)







