The technique for producing polarized beams depends not only on the particle species, but also on their kinetic energies. For stable ones, such as electrons or protons, polarized sources can be employed with subsequent acceleration in a linear accelerator or a synchrotron. For unstable particles, like muons, polarization-dependent particle decays are exploited[
High Power Laser Science and Engineering, Volume. 8, Issue 4, 04000e36(2020)
Generation of polarized particle beams at relativistic laser intensities

The acceleration of polarized electrons, positrons, protons and ions in strong laser and plasma fields is a very attractive option for obtaining polarized beams in the multi-mega-electron volt range. Recently, there has been substantial progress in the understanding of the dominant mechanisms leading to high degrees of polarization, in the numerical modeling of these processes and in their experimental implementation. This review paper presents an overview on the current state of the field, and on the concepts of polarized laser–plasma accelerators and of beam polarimetry.
1 The need for polarized beams
![]()
Figure 1.Scenario of the generation of spin-polarized electron beams via nonlinear Compton scattering: a relativistic electron bunch generated by laser-wakefield acceleration collides head-on with an elliptically polarized laser pulse and splits along the propagation direction into two parts with opposite transverse polarization[34]. OAP, optical parametric amplification.
All of the above scenarios still rely on conventional particle accelerators that are typically very large in scale and budget[
Concepts based on laser-driven acceleration at extreme light intensities have been promoted during recent decades. Ultra-intense and ultra-short laser pulses can generate accelerating fields in plasmas that are at the order of tera-volts per meter, about four orders of magnitude greater compared to conventional accelerators. The goal, therefore, is to build the next generation of highly compact and cost-effective accelerator facilities using a plasma as the accelerating medium; see for example Ref. [33]. Despite many advances in the understanding of the phenomena leading to particle acceleration in laser–plasma interactions, however, a largely unexplored issue is how an accelerator for strongly polarized beams can be realized. In simple words, there are two possible scenarios: either the magnetic laser or plasma fields can influence the spin of the accelerated beam particles, or the spins are too inert, such that a short acceleration has no influence on the spin alignment. In the latter case, the polarization would be maintained throughout the whole acceleration process, but a pre-polarized target would be required.
Sign up for High Power Laser Science and Engineering TOC Get the latest issue of High Power Laser Science and Engineering delivered right to you!Sign up now
In this paper, we review the concepts and methods that could lead to the generation of polarized particle beams based on ultra-intense lasers. We focus on two main approaches. The first one is devoted to collision between unpolarized high-energy electron beams and ultra-relativistic laser pulses, introduced in Section 2.1. Section 2.2 focuses on concepts for pre-polarized targets for sequential particle acceleration. Suitable targets are described in Section 7.
2 Concepts
2.1 Polarization build-up from interactions with relativistic laser pulses
Strong-field quantum electrodynamics (QED) processes – like nonlinear Compton scattering and radiation reactions – can strongly modify the dynamics of light charged particles, such as electrons or positrons. Analogous to the Sokolov–Ternov effect in a strong magnetic field, electrons can rapidly spin-polarize in ultra-strong laser fields due to an asymmetry in the rate of spin-flip transitions, i.e., interactions where the spin changes sign during the emission of a γ-ray photon. Several such scenarios have been discussed in the literature; for a more quantitative discussion we refer to Section 4.
![]()
Figure 2.Schematic representation of electron spin polarization employing the standing wave of two colliding, circularly polarized laser pulses[39].
![]()
Figure 3.Electrons propagating through a bichromatic laser pulse perform spin-flips dominantly in certain phases of the field: electrons initially polarized along the +
![]()
Figure 4.Scheme for laser-based polarized positron beam production[42].
2.2 Polarized beams from pre-polarized targets
![]()
Figure 5.Sketch of the all-optical laser-driven polarized electron acceleration scheme using a pre-polarized target[46]. LG, Laguerre–Gaussian; OAP, optical parametric amplification.
![]()
Figure 6.Schematic diagram showing laser acceleration of polarized protons from a dense hydrogen chloride gas target (brown). HCl molecules are initially aligned along the accelerating laser (indicated by the green area) propagation direction via a weak infrared (IR) laser. Blue and white balls represent the nuclei of hydrogen and chlorine atoms, respectively. Before the acceleration, a weak circularly polarized UV laser (purple area) is used to generate the polarized atoms along the longitudinal direction via molecular photo-dissociation. The brown curve indicates the initial density distribution of the gas-jet target. The polarized proton beam is shown on the right (blue) with arrows (red) presenting the polarization direction[54].
![]()
Figure 7.Measured 3,4He2+ energy spectra accelerated from unpolarized helium gas jets[56]. IP, image plate.
3 Theoretical background
It is still an issue for current research how particle spins are affected by the huge electromagnetic fields that are inherently present in laser-induced plasmas or in the laser fields themselves, and what mechanisms may lead to the production of highly polarized beams. Early attempts to describe these processes can be found in Refs. [47,58]. A schematic overview of the interplay between single particle trajectories (blue), spin (red) and radiation (yellow) is shown in Figure 8; details can be found in Ref. [48].
![]()
Figure 8.Sketch of the interplay between single particle trajectories (blue), spin (red) and radiation (yellow)[48].
In cgs units the rotational frequency
 (2)
(2)where
 (3)
(3)Spin precession is a deterministic process and can be calulated by treating the spin as an intrinsic electron magnetic moment. In the non-QED regime, only a theory, which contains the T–BMT equation, describes the particle and spin motion in electromagnetic fields in a self-consistent way.
Under classical and semi-classical limits, the acceleration of charged particles is treated within the framework of classical field theory. This theory also describes the reaction of the particle motion due to radiation, if the particle energy and/or laser field strength is sufficiently high. Introducing spin into electron dynamics leads to a spin-dependent radiation reaction. The radiation power of electrons in different spin states varies such that they feel a stronger radiation-reaction force when the spins are anti-parallel to the local magnetic field in the rest frame of the radiating electron, which can lead to a split of electrons with distinctive spin states.
The Stern–Gerlach force primarily influences the trajectory of a particle. In general, the radiation-reaction force exceeds the Stern–Gerlach force by far if the particles are relativistic (kinetic energies well above 1 GeV) or even ultra-relativistic (above 1 TeV) (see also Ref. [36]). There are, however, some field configurations that reverse this situation, so that the radiation-reaction force can be neglected compared to the Stern–Gerlach force (see e.g., Ref. [61]).
A direct coupling between single particle spins and radiation fields is treated in the context of quantum field theory. Within this theory, the mechanism that describes the spontaneous self-polarization of an accelerated particle ensemble is known as the Sokolov–Ternov effect. The stochastic spin diffusion from photon emission is a non-deterministic process resulting in the rotation of the spin vector in the presence of a magnetic field with the emission of a photon.
A discussion of the generalized Stern–Gerlach force shows that the trajectories of individual particles are perturbed by a change of the particle’s motion induced by the T–BMT equation rather than by coupling of the spin to the change of the particles’ energy or velocity rates; while even small field variations must be taken into account[
Del Sorbo et al.[
Description of the spin-dependent dynamics and radiation in optical laser fields requires a classical spin vector that precesses during photon emission events following the T–BMT equation. This is accomplished by projecting the spin states after each emission onto a quantization axis. The latter could be the local magnetic field in the rest frame of the radiating electron[
4 Model calculations I: strong field QED
![]()
Figure 9.(a) Transverse distribution of the electron spin component
In a follow-up paper, Guo et al.[
Another paper from Li et al.[
![]()
Figure 10.Achievable degree of electron polarization as a function of a quantum nonlinearity parameter 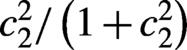 ). The calculations have been performed for 5 GeV electrons colliding with a 161 fs laser pulse, i.e.,
). The calculations have been performed for 5 GeV electrons colliding with a 161 fs laser pulse, i.e.,
![]()
Figure 11.Average polarization
For positrons, rather high degrees of polarization seem to be achievable, even for currently achievable laser parameters. Chen et al.[
5 Model calculations II: particle-in-cell simulations
5.1 Electron acceleration
Wen et al.[
![]()
Figure 12.Prediction from Wu
![]()
Figure 13.Electron polarization distributions in the transverse phase space during laser-wakefield acceleration[49].
5.2 Heavy particles
![]()
Figure 14.Three-dimensional PIC simulation of proton acceleration assuming a gaseous HCl target with a hydrogen density of 8.5 × 1019 cm−3 and a circularly polarized laser pulse with 800 nm wavelength and a normalized amplitude of
![]()
Figure 15.(a) Three-dimensional PIC simulation for a gaseous HCl target with molecular density of 1019 cm−3 and 1.3 PW laser with phase-space distribution; (b) spin spread of protons with energy
![]()
Figure 16.Simulated normalized He2+ ion-number density during the passage of a peta-watt laser pulse (6.5 ps after it entered the simulation box at the left boundary) through an unpolarized helium gas jet target. (a) 2%; (b) 3%; (c) 4%; (d) 12% critical density[56].
6 Lessons learned from theoretical studies
From the literature outlined in Sections 2–5 it becomes clear that a wealth of (mostly theoretical) pathways towards the realization of laser-induced polarized particle acceleration have been put forward in recent years. These concepts strongly differ for the various particle species. In some cases it is necessary to wait for significant progress in laser technology. Our conclusions for a strategy aiming at the speedy realization of laser-induced polarized particle acceleration are given below.
- (1)For currently realistic laser parameters, pre-polarized targets are needed to achieve electron beams with polarizations well above 10%. Such targets should provide high degrees of electronic polarization (> 50%) and should allow for operation at laser facilities (e.g., robustness against electromagnetic pulses (EMPs) and target heating).
- (2)Due to their three-orders-smaller magnetic moments, measurable polarization for heavier particles (protons, ions) can only be achieved with nuclear pre-polarized targets.
- (3)For positrons, no pre-polarized targets can be realized. Here, high degrees of polarization (90%) can be obtained from the scattering of peta-watt laser pulses off an unpolarized relativistic electron beam (which can be laser-generated). Such schemes require precise control of all involved beam pointings (to the few-milliradian level).
- (4)Gas-jet targets are preferable to foil targets since they allow operation with state-of-the-art kilo-hertz laser systems. Low-density targets are also less challenging in terms of depolarizing effects.
7 Experimental techniques I: polarized targets
For the experimental realization of polarized beam generation from laser-induced plasmas, the choice of the target is a crucial point. Pre-polarized solid foil targets suitable for laser acceleration via target normal sheath acceleration (TNSA) or radiation-pressure acceleration (RPA) are not yet available, and their realization seems extremely challenging. In previous experiments, hydrogen nuclear polarization has mostly been realized through a static polarization, e.g., in frozen spin targets[
7.1 Static polarization: 3He
![]()
Figure 17.Perspective view of the 3D model of the fully mounted magnetic system inside the PHELIX chamber[57,67].
The magnetic holding field consists of an outer Halbach array composed of an upper and lower ring of 48 NdFeB permanent magnets, 1100 mm in diameter, together with an inner Helmholtz coil array consisting of four single Helmholtz coils. In the Halbach array the permanent magnets are stacked at an optimum distance such that its field homogeneity is sufficiently high to maintain nuclear 3He polarization. The Helmholtz coils are oriented so that their magnetic field is aligned parallel to the laser-propagation direction. A single coil consists of a coiled Cu sheet with a width and thickness of 40 mm. The outer and inner diameters of the naked Cu coil are 789 mm and 709 mm, respectively. Both inner coils are separated by 285.75 mm, while the two single front/rear coils are separated by a distance of 218.95 mm. In contrast to electric coils, the permanent magnets used do not need to be cooled in vacuum, and they provide a constant field, even in the presence of huge EMPs[
The second essential component for the layout of a polarized 3He target is the gas-jet source. The pre-polarized 3He gas is delivered at an intrinsic pressure of 3 bar. By using a pressure booster built of non-magnetic materials, the desired final pressure can be reached (up to 30 bar). To synchronize the gas flux with the incoming laser pulse, a home-made non-magnetic valve with piezo actuators has been prepared. In order to generate a broad plateau-like density distribution with sharp density gradients, a supersonic de Laval nozzle is used.
7.2 Dynamic polarization: protons and electrons
![]()
Figure 18.The 1064 nm IR laser propagates along the
![]()
Figure 19.Technical drawing of the optical setup including the JuSPARC_MIRA laser system and the target chamber for the polarized proton target[64].
The fifth-harmonic beam is guided by customized optics with the highest possible light reflectance (reflection > 98% at 45° incidence angle provided by Layertec GmbH) having a diameter of one inch for a beam diameter of 12 mm. A quartz quarter-wave plate with two-sided anti-reflection coating from EKSMA Optics converts the initially linearly polarized laser beam to circular polarization. Finally, the UV beam is focused below the HCl or HBr nozzle inside the interaction chamber. The fundamental beam at 1064 nm is guided by standard mirrors with dielectric Nd:YAG coatings and focused to an intensity of about 5 × 1013 W·cm−2 into the HCl or HBr gas. The gas is injected into the interaction chamber by a high-speed short-pulse piezo valve that can be operated at a maximum 5 bar inlet gas pressure to produce a gas density in the range of about 1019 cm−3[51,64]. The valve is adjustable in height so that sufficient amounts of HCl or HBr molecules, which are spread in a cone-like shape, interact with the laser beams by keeping the backing pressure low, and thus the molecules’ mean free path large enough.
7.3 Hyperpolarized cryogenic targets
![]()
Figure 20.Schematic view of the interaction chamber for production and storage of polarized H2, D2, HD and 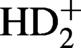 foils[71].
foils[71].
In the next step, a small pipe, to include an independent cooling and power supply, will be installed on one side of the cell having no direct contact with the cell. In this way, molecules can be generated and pre-cooled in the storage cell before they are frozen in the new pipe. Thus, the molecules in the storage cell can still be ionized and accelerated to measure their polarization. After the atomic flow is stopped, the pipe slowly warms up. In this way, the polarization of the molecules that have been frozen can be measured to compare the polarization values of the just-recombined molecules and those that are frozen into ice. The residual gas is pumped by cryogenic panels below 10−8 mbar without gas load to the cell. Using a superconducting solenoid at a temperature of 4 K, a magnetic field of up to 1 T in the storage cell can be generated. Additionally, it focuses an electron beam, which is produced by an electron gun at energies of a few 100 eV on the left side of the apparatus. The interaction of the polarized atoms and evaporated molecules with the electron beam results in an ionization process. Next, the ionized protons and
8 Experimental techniques II: beam polarimetry
In order to experimentally determine the degree of polarization of laser-accelerated particle bunches, dedicated polarimeters must be used. Similar devices are widely used in particle physics, for example to determine beam polarizations at classical accelerators. They are typically based on a scattering process with known analyzing power, which converts the information about the beam polarization into a measurable azimuthal angular asymmetry. In the case of laser-accelerated particles, however, a couple of peculiar requirements have to be taken into account.
- (1)Due to the time structure of the laser pulses, all scattered particles hit the detector within a few tens of femtoseconds. Thus, it must be virtually dead-time free or, more realistically, all particle signals from one laser shot must be integrated up.
- (2)The detectors must have a high EMP robustness. This is especially challenging for electronic detectors with an on-line readout.
- (3)A high angular resolution is required in some cases; see Figure 9.
- (4)Depending on the phase-space densities of the accelerated particles, it may be required to measure small particle numbers (per laser shot); see Ref. [72].
8.1 Proton and ion polarimetry
![]()
Figure 21.Schematic view of the setup for proton polarization measurements by Raab
For the polarimetry of protons with higher kinetic energies, CH2 (polypropylene foils), rather than silicon, is the proper material for the polarimeter. A new proton polarimeter is now being commissioned and calibrated with polarized protons at COSY-Jülich, where beam energies from 45 MeV up to 2.88 GeV are available.
8.2 Electron polarimetry
Depending on the electron beam energy, which determines the analyzing power as well as experimental access to the scattering products, one of the following spin-dependent QED processes can be used for electron polarimetry[
- (1)Mott scattering[
74 –76 ], i.e., scattering off the nuclei in a target, used for beams between 10 keV and 1 MeV, often for polarimetry of electron sources at large accelerators. - (2)Bremsstrahlung emission in a target[
77 ], used from about 10 MeV to a few 100 MeV, relies on measuring the degree of circular polarization of photons generated when passing the beam through a thin target[78 ]. Statistical significance of the order of 10% can be achieved. - (3)Møller (or for positron beams Bhabha) scattering[
79 ], i.e., scattering off the electrons in a target, used from a few 100 MeV to GeV energies in fixed target experiments at SLAC[80 –83 ] and JLab[84 ], but also at ELSA[85 ] and MAMI[86 ]. Precisions down to 0.5% can be reached[87 ]. - (4)Compton scattering[
88 ], i.e., scattering off a laser, used for GeV and higher energies, offers high analyzing power$\mathcal{O}(1)$ 89 ] and robust control over experimental systematics. Long-established for measuring longitudinal and transverse polarization, e.g., at SLC[90 ], LEP[91 ], HERA[25 ,92 ], ELSA[93 ], MAMI[94 ] and JLab[95 ], it is also the method of choice for future colliders[96 –98 ]. Precisions from a few percent down to a few permil can be reached.
The short bunch length typical for plasma-accelerated beams is not a problem for any of these methods; rather, it is an advantage. All methods apart from Compton scattering are destructive. Due to the typical energies obtained in laser-wakefield experiments, method 2 is the most applicable technique for diagnosing the degree of polarization of such beams. A new polarimeter for measuring polarization of laser-plasma accelerated electrons is being designed and constructed at DESY.
9 Summary and outlook
In this review paper we discuss the current status of polarized beam generation, including polarization techniques for conventional accelerators, new ideas for laser-based accelerator facilities at relativistic laser intensities and corresponding concepts for beam polarimetry.
Polarized particle beams are an important tool in nuclear and particle physics for the study of the interaction and structure of matter and to test the Standard Model of particle physics. All techniques to deliver polarized beams for such applications are currently based on conventional particle accelerators. Unfortunately, these are typically very large in size and devour huge financial resources.
Novel concepts based on laser-driven acceleration at extreme intensities have been investigated intensively over recent decades. The advantage of laser-driven accelerators is the capability to provide accelerating fields up to tera-volts per meter, about four orders of magnitude greater than conventional ones. It is therefore a highly desirable objective to build the next generation of compact and cost-effective accelerator facilities making use of laser-plasma techniques.
To get a deeper understanding of the processes leading to polarized beam production, theoretical and experimental work is gaining momentum. First of all, particle spins subject to the huge magnetic fields of laser-plasma accelerators can be monitored in theoretical studies using PIC simulations. More comprehensive tests of QED-based models have also been made to account for the radiative polarization and spin-dependent reaction effects. Much more theoretical and experimental work needs to be done to obtain a complete picture of spin motion in ultra-strong relativistic electromagnetic fields.
Simulations and analytical estimates indicate that light particles like electrons can be either polarized directly by strong laser-plasma fields or preserve polarization from pre-polarized targets. In contrast, heavy particles like protons and ions require the latter. The first such targets, which are tailored to laser applications, are in the commissioning phase. Therefore, the first successful experiments at currently available laser intensities are to be expected within the next few years. In view of this, it seems advisable to foresee options for polarized beams for the planning of next-generation accelerator facilities.
[1] G. Moortgat-Pick, T. Abe, G. Alexanderet al.,. Phys. Rep., 460, 131(2008).
[2] F. Rathmann, A. Saleev, N. N. Nikolaev. J. Phys. Conf. Ser., 447(2013).
[3] J. Grange, V. Guarino, P. Winter et al. , , , arXiv:1501.06858 ().(2015).
[4] D. Androić, D. S. Armstrong, A. Asaturyanet al.,. Nature, 557(2018).
[5] M. Burkardt, C. A. Miller, W. D. Nowak. Rep. Prog. Phys., 73(2010).
[6] E. S. Ageev, V. Y. Alexakhin, Y. Alexandrovet al.,. Phys. Lett. B, 612, 154(2005).
[7] C. Glashausser. Ann. Rev. Nucl. Part. Sci., 29, 33(1979).
[8] R. L. Jaffe. Int. J. Mod. Phys. A, 18, 1141(2003).
[9] H. Baer, T. Barklow, K. Fujii et al. , , , , arXiv:1306.6352 ().(2013).
[10] P. Adlarson. WASA-at-COSY Collaboration. Phys. Rev. Lett., 112, 202301(2014).
[11] T. J. Gay.
[12] B. Bederson.
[13] F. Rathmann, P. Lenisa, E. Steffens et al. Phys. Rev. Lett., 94, 014801(2005).
[14] A. A. Sokolov, I. M. Ternov. Sov. Phys. Dokl., 8, 1203(1964).
[15] A. A. Sokolov, D. V. Geltsov, M. M. Kolesnikova. Sov. Phys. J., 14(1971).
[16] S. R. Mane, Y. M. Shatunov, K. Yokoya. Rep. Prog. Phys., 68, 1997(2005).
[17] Proceedings of the 8th International Conference on High-Energy Acceleratorsin (), p. 127.(1971).
[18] V. N. Baier. Sov. Phys. Usp., 14, 695(1972).
[19] U. Camerini, D. Cline, J. Learned et al. Phys. Rev. D, 12, 1855(1975).
[20] C. Steier, D. HusmannProceedings of Particle Accelerator Conference. and , in (), p. 1033.(1988).
[21] C. W. Leemann, D. R. Douglas, G. A. Krafft. Ann. Rev. Nucl. Part. Sci., 51, 413(2001).
[22] W. W. MacKay, J. F. Hassard, R. T. Giles et al. Phys. Rev. D, 29, 2483(1984).
[23] R. Assmann, J. P. Koutchouk. Divisional Report CERN SL/94-13 AP(1994).
[24] D. P. Barber, H.-D. Bremer, M. BögeProceedings of the 2nd European Particle Accelerator Conference. , , , , in (), paper M-90-05.(1990).
[25] D. P. Barber, H.-D. Bremer, M. Böge et al. Nucl. Instrum. Meth. A, 329, 79(1993).
[26] T. Khoe, R. L. Kustom, R. L. Martin et al. Part. Accel., 6, 213(1975).
[27] F. Z. Khiari, P. R. Cameron, G. R. Court et al. Phys. Rev. D, 39, 45(1989).
[28] H. Sato, D. Arakawa, S. Hiramatsu et al. Nucl. Instrum. Meth. A, 272, 617(1988).
[29] D. L. Friesel, V. Derenchuk, T. SloanProceedings of the European Accelerator Conference. , , , , in (), p. ., 539(2000).
[30] T. Aniel, J. L. Laclare, G. Leleux et al. J. Phys. Colloq., 46, 499(1985).
[31] I. Alekseev, C. Allgower, M. Bai et al. Nucl. Instrum. Meth., 499, 392(2003).
[32] A. Lehrach, U. Bechstedt, J. Dietrich et al. AIP Conf. Proc., 675, 153(2003).
[33] P. A. Walker, P. D. Alesini, A. S. Alexandrova et al. J. Phys. Conf. Ser., 874(2017).
[34] Y.-F. Li, R. Shaisultanov, K. Z. Hatsagortsyan et al. Phys. Rev. Lett., 122, 154801(2019).
[35] R.-T. Guo, Yu. Wang, R. Shaisultanov et al. Phys. Rev. Res., 2(2020).
[36] X. S. Geng, L. L. Ji, B. F. Shen et al. New J. Phys., 22(2020).
[37] D. Del Sorbo, D. Seipt, T. G. Blackburn et al. Phys. Rev. A, 96(2017).
[38] D. Seipt, D. Del Sorbo, C. P. Ridgers et al. Phys. Rev. A, 98(2018).
[39] D. Del Sorbo, D. Seipt, A. G. R. Thomas et al. Plasma Phys. Control. Fusion, 6(2018).
[40] D. Seipt, D. Del Sorbo, C. P. Ridgers et al. Phys. Rev. A, 100(2019).
[41] H.-H. Song, W.-M. Wang, J.-X. Li et al. Phys. Rev. A, 100(2019).
[42] Y.-Y. Chen, P.-L. He, R. Shaisultanov et al. Phys. Rev. Lett., 123(2019).
[43] F. Wan, R. Shaisultanov, Y.-F. Li et al. Phys. Lett. B, 800(2020).
[44] Y.-F. Li, Y.-Y. Chen, W.-M. Wang et al. Phys. Rev. Lett., 125.
[45] M. Wen, M. Tamburini, C. H. Keitel. Phys. Rev. Lett., 122, 214801(2019).
[46] Y. Wu, L. Ji, X. Geng et al. New J. Phys., 21(2019).
[47] J. Vieira, C.-K. Huang, W. B. Mori et al. Phys. Rev. Accel. Beams, 14(2011).
[48] J. Thomas, A. Hützen, A. Lehrach et al. Phys. Rev. Accel. Beams, 23(2020).
[49] Y. Wu, L. Ji, X. Geng et al. Phys. Rev. Appl., 13(2020).
[50] Y. Wu, L. Ji, X. Geng et al. Phys. Rev. E, 100(2019).
[51] A. Hützen, J. Thomas, J. Böker et al. High Power Laser. Sci. Eng., 7(2019).
[52] M. Büscher, A. Hützen, I. Engin et al. Int. J. Mod. Phys. A, 34(2019).
[53] A. Hützen, J. Thomas, A. Lehrach et al. , , , , J. Phys. Conf. Ser. , ()., 1596(2020).
[54] L. Jin, M. Wen, X. Zhang et al. Phys. Rev. E, 102(2020).
[55] I. Engin, M. Büscher, O. DeppertProceeding of the XVIth International Workshop in Polarized Sources, Targets, and Polarimetry. , , , , in (), paper 002.(2015).
[56] I. Engin, Z. M. Chitgar, O. Deppert et al. Plasma Phys. Control. Fusion, 61(2019).
[57] G. Ciullo, R. Engels, M. Büscher et al. Nuclear Fusion with Polarized Fuel(2016).
[58] G. L. Kotkin, V. G. Serbo, V. I. Telnov. Phys. Rev. Accel. Beams, 6(2003).
[59] L. H. Thomas. Phil. Mag., 3(1927).
[60] V. Bargmann, L. Michel, V. L. Telegdi. Phys. Rev. Lett., 2(1959).
[61] S. P. Flood, D. A. Burton. Phys. Lett. A, 379, 1966(2015).
[62] X. S. Geng, Z. G. Bu, Y. T. Wu et al. , , , , arXiv:1912.03625 ().(2020).
[63] Y.-F. Li, R.-T. Guo, R. Shaisultanov et al. Phys. Rev. Appl., 12(2019).
[64] J. Forschungszentrum Jülich. Large-Scale Res. Facil., 6, A138(2020).
[65] C. D. Keith, J. Brock, C. Carlin et al. Nucl. Instrum. Meth., 684(2012).
[66] A. Nass, C. Baumgarten, B. Braun et al. Nucl. Instrum. Meth, 505, 633(2003).
[67] I. EnginTowards Polarization Measurements of Laser-accelerated Helium-3 Ions. , , PhD. Thesis (Heinrich Heine University Düsseldorf, ).(2015).
[68] H. Soltner, M. Büscher, P. Burgmer et al. IEEE Trans. Appl. Supercond., 26(2016).
[69] D. Sofikitis, L. Rubio-Lago, M. R. Martin et al. Phys. Rev. A, 76(2007).
[70] D. Sofikitis, L. Bougas, G. E. Katsoprinakis et al. Nature, 514(2014).
[71] R. Engels, H. M. Awwad, S. ClausenProceedings of the 23rd International Spin Physics Symposium. , , , , in (), paper 099.(2018).
[72] N. Raab, M. Büscher, M. Cerchez et al. Phys. Plasmas, 21(2014).
[73] K. Aulenbacher, E. Chudakov, D. Gaskell et al. Int. J. Mod. Phys. E, 27, 1830004(2018).
[74] N. F. Mott. Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci., 124, 424(1929).
[75] J. Kessler. Rev. Mod. Phys., 41, 3(1969).
[76] T. J. Gay. Rev. Sci. Instrum., 63, 1635(1992).
[77] H. Olsen, L. Maximon. Phys. Rev., 114, 887(1959).
[78] G. Alexander, J. Barley, Y. Batygin et al. Nucl. Instrum. Meth. A, 610, 451(2009).
[79] J. D. Ullman, H. Frauenfelder, H. J. Lipkin et al. Phys. Rev., 122, 536(1961).
[80] P. Cooper, M. Alguard, R. Ehrlich et al. Phys. Rev. Lett., 34, 1589(1975).
[81] H. Band, G. Mitchell, R. Prepost et al. Nucl. Instrum. Meth. A, 400, 24(1997).
[82] P. Steiner, A. Feltham, I. Sick et al. Nucl. Instrum. Meth. A, 419, 105(1998).
[83] P. Anthony. Phys. Rev. Lett., 95(2005).
[84] N. Baltzell, V. Burkert, J. Carvajal et al. Nucl. Instrum. Meth. A, 959(2020).
[85] T. Speckner, G. Anton, W. Drachenfels et al. Nucl. Instrum. Meth. A, 519, 518(2004).
[86] B. Wagner, H. Andresen, K. Steffens et al. Nucl. Instrum. Meth. A, 294, 541(1990).
[87] M. Hauger, A. Honegger, J. Jourdan et al. Nucl. Instrum. Meth. A, 462, 382(2001).
[88] U. Fano. , J. Opt. Soc. Am. , ()., 39, 859(1949).
[89] M. L. Swartz. Phys. Rev. D, 58(1998).
[90] K. Abe, K. Abe, T. Abe et al. Phys. Rev. Lett., 84, 5945(2000).
[91] M. Placidi, R. Rossmanith. Nucl. Instrum. Meth. A, 274, 79(1989).
[92] D. P. Barber, M. Böge, H.-D. Bremer et al. Phys. Lett. B, 343, 436(1995).
[93] D. DollDas Compton-Polarimeter an ELSA. , , PhD. Thesis (Bonn University, ).(1998).
[94] J. H. LeeConcept and Realization of the A4 Compton Backscattering Polarimeter at MAMI. , , PhD. Thesis (Mainz University, ).(2008).
[95] A. Narayan, D. Jones, J. C. Cornejo et al. Phys. Rev. X, 6(2016).
[96] S. Boogert, A. F. Hartin, M. Hildreth et al. JINST, 4, P10015(2009).
[97] C. Adolphsen, M. Barone, B. Barish et al. , , , , arXiv:1306.6328 ().(2013).
[98] M. Aicheler, P. Burrows, M. Draper et al. A Multi-TeV Linear Collider Based on CLIC Technology: CLIC Conceptual Design Report(2012).
Get Citation
Copy Citation Text
Markus Büscher, Anna Hützen, Liangliang Ji, Andreas Lehrach. Generation of polarized particle beams at relativistic laser intensities[J]. High Power Laser Science and Engineering, 2020, 8(4): 04000e36
Special Issue: SPECIAL ISSUE ON 60TH CELEBRATION OF FIRST LASER
Received: Jun. 12, 2020
Accepted: Aug. 25, 2020
Posted: Aug. 26, 2020
Published Online: Nov. 23, 2020
The Author Email: Markus Büscher (m.buescher@fz-juelich.de), Liangliang Ji (jill@siom.ac.cn)






